22. Дифференциальные уравнения

22.1. Дифференциальные уравнения первого

порядка. Дифференциальные уравнения

с разделяющимися переменными

Пусть x– независимая переменная,y(x) – функция от переменнойx, заданная на некотором промежутке.

Дифференциальным уравнением(обыкновенным дифференциальным уравнением) называется уравнение, связывающее независимую переменнуюx, функциюy(x) и ее производные.

Порядкомдифференциального уравнения называется наивысший порядок производной, входящей в него.

Дифференциальное уравнение 1-го порядка имеет вид:

(22.1)

где F– некоторое выражение относительноx, искомой функцииy(x) и ее производной, заданное в области

Если дифференциальное уравнение разрешено относительно производной функции, то его общий вид:

(22.2)

где f– некоторое выражение относительноxиy,В таком случае говорят, что дифференциальное уравнение записано внормальном виде.

Решениемдифференциального уравнения называется такая дифференцируемая функциякоторая обращает это уравнение в тождество.

Поиск решения дифференциального уравнения называется интегрированием дифференциального уравнения, а график этого решения –интегральной кривой.

Начальным условием(условием Коши) называется условиекоторым задается дополнительное требование на решениеy(x) дифференциального уравнения.

Общим решениемдифференциального уравнения (22.2) в областиназывается функцияудовлетворяющая условиям:

1) является решением данного дифференциального уравнения при любом значении произвольной постояннойС;

2) для любого начального условия такого, чтосуществует единственное значениепри котором решениеудовлетворяет начальному условию.

Общее решение заданное в неявном виде, называетсяобщим интегралом дифференциального уравнения.

Частным решением дифференциального уравнения называется всякое решение, полученное из общего при конкретном значении

Задачей Кошиназывается задача отыскания частного решения дифференциального уравнения, удовлетворяющего заданному начальному условиюГеометрически общему решению на координатной плоскости соответствует семейство интегральных кривыхзависящее от числового параметраС, а частному решению – определенная интегральная кривая, проходящая через точку

Теорема Коши. Если функцияf(x, y) непрерывна и имеет непрерывную производнуюв областиD, то решение дифференциального уравнения (22.2) при начальном условиисуществует и единственно.

Решение дифференциального уравнения, во всех точках которого не выполняется условие единственности, называется особым решением. Особое решение не может быть получено из общего решения дифференциального уравнения ни при каком значении произвольной постояннойC.

Дифференциальное уравнение вида

(22.3)

где  – функции переменной x, – функции пере­меннойy, называется уравнением с разделяющимися пере­менными.

Для решения уравнения (22.3) предполагают иПочленным делением уравнения (22.3) наего сводят к уравнению

(22.4)

которое в левой части содержит выражение только от переменной x, а в правой – только от переменнойy(этим объясняется название данного типа дифференциальных уравнений). Далее интегрируют равенство (22.4) (слева – по переменнойx, а справа – поy) и получают общее решение.

Ограничения могут привести к потере решений, поэтому следует решить уравненияии установить подстановкой в заданное дифференциальное уравнение, являются ли они решением дифференциального уравнения. Затем необходимо определить, входят ли они в общее решение (или являются особыми).

Пример 1. Доказать, что функция является решением дифференциального уравнения

Решение. Продифференцируем функцию:Подставим ее в заданное дифференциальное уравнение:

В итоге получаем тождество

или

Это доказывает, что функция является решением заданного дифференциального уравнения.

Пример 2. Доказать, что равенство является общим интегралом дифференциального уравнения

Решение. Вычислим производную неявной функции по формуле

поскольку то

Подставим ив заданное дифференциальное уравнение:

Получили тождество что и доказывает требуемое.

Пример 3. Найти общее решение дифференциального уравнения:

1) 2)3)

Решение. 1) Используем то, что и запишем исходное дифференциальное уравнение в виде

или

Так как для всехто преобразуем уравнение к виду

Интегрируем последнее равенство: Получаем– общее решение заданного дифференциального уравнения.

2) Предполагаем, что а так какдля всехто преобразуем заданное дифференциальное уравнение к виду

Интегрируем последнее равенство:

Получаем:

Произвольную константу записали в форме lnC для удобства дальнейших преобразований:

т. е.

Заметим, что преобразования аналитических выражений производятся с точностью до константы C.

Таким образом, – общее решение исходного дифференциального уравнения.

Проверяем, является ли решением Подставляем в заданное дифференциальное уравнение и видим, чтоявляется решением дифференциального уравнения. Однако оно не является особым, так как получается из общего решения при

Приходим к ответу:

–общее решение, С = const.

3) Используя то, что запишем уравнение в виде

Предполагаем, что и преобразуем уравнение к видуИспользуя формулу тригонометрииинтегрируем последнее равенство:

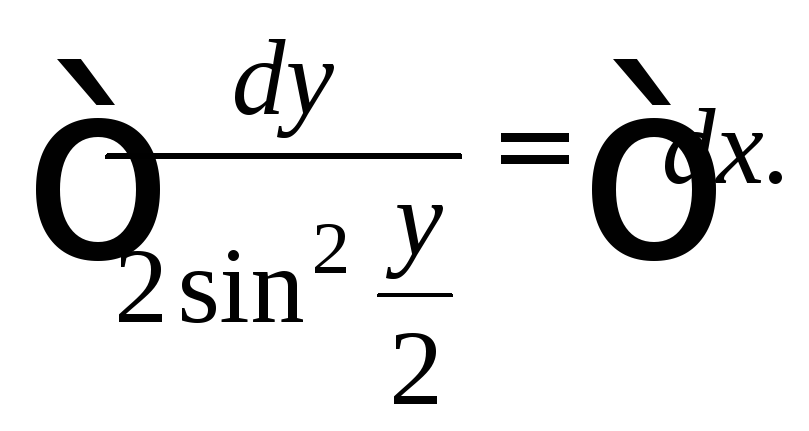
Имеем:

или

Таким образом, получаем – общее решение исходного дифференциального уравнения.

Проверяем, дает ли равенство особые решения. Получаем,– это есть особые решения исходного дифференциального уравнения. Таким образом, решение заданного дифференциального уравнения:

Пример 4. Известно, что решением некоторого дифференциального уравнения является семейство парабол Определить это дифференциальное уравнение.

Решение. Дифференцируя равенство имеем

(22.5)

Выразим C из уравнения параболы: Подставив найденное значениеС в уравнение (22.5), получим т. е.

(22.6)

Заданное семейство парабол является решением дифференциального уравнения (22.6).

Пример 5. Доказать, что является общим интегралом дифференциального уравненияОпределить частные интегралы, если известно, что интегральные кривые проходят соответственно через точки (0, – 1) и (2, 0), построить эти кривые.

Решение. Вычислим производную неявной функции по формуле

где

Тогда Подставим и в заданное дифференциальное уравнение:

или

Получили тождество Это доказывает, что заданная неявно функция является общим интегралом исходного дифференциального уравнения. Для нахождения частных интегралов и проходящих через заданные точки интегральных кривых подставляем координаты этих точек в общий интеграл и определяем соответствующие константы.

Для точки (0, – 1) получаем: илиДля точки (2, 0) получаем:илиТогда частными интегралами будут:

и

Интегральными кривыми являются концентрические окружности с центром в точке и радиусами 2 и 1 соответственно. Это видно, если в полученных частных интегралах выделить полный квадрат поx и по y:

Графики интегральных кривых изображены на рис. 22.1.

Рис. 22.1

Пример 6. Найти частное решение дифференциального уравнения:

1) 2)

3)

Решение. 1) Разделив уравнение на получим:

Интегрируем левую и правую части:

Получаем – общее решение исходного дифференциального уравнения. Подставляем начальное условиеи находим константуС:

или

Нашли частное решение

2) Преобразуя заданное уравнение с учетом того, что получаемДалее интегрируем:

или – это общий интеграл исходного уравнения.

Используем начальное условие: в полученное решение подставляем иНаходим константуС:

т. е. Значит,откуда получаем:

–искомое частное решение (частный интеграл).

3) С учетом равенства получаемИнтегрируем:илиВычисляем последний интеграл, дважды интегрируя по частям:

Отсюда получаем

Таким образом, – общее решение исходного дифференциального уравнения. Подставляя в негонаходимС: т. е.Частным решением является

Задания