
- •22. Дифференциальные уравнения
- •22.1. Дифференциальные уравнения первого
- •I уровень
- •II уровень
- •III уровень
- •22.2. Однородные дифференциальные
- •I уровень
- •II уровень
- •III уровень
- •22.3. Линейные уравнения. Уравнение Бернулли
- •I уровень
- •II уровень
- •III уровень
- •22.4. Уравнения в полных дифференциалах
- •I уровень
- •II уровень
- •III уровень
- •22.5. Понятие дифференциальных уравнений
- •I уровень
- •II уровень
- •III уровень
- •22.6. Линейные однородные дифференциальные
- •I уровень
- •II уровень
- •III уровень
- •22.7. Линейные неоднородные дифференциальные
- •I уровень
- •II уровень
- •III уровень
- •22.8. Системы дифференциальных уравнений
- •22.9. Системы линейных однородных
- •I уровень
- •II уровень
- •III уровень
- •Содержание
I уровень
1.1.Решите систему дифференциальных уравнений:
1)
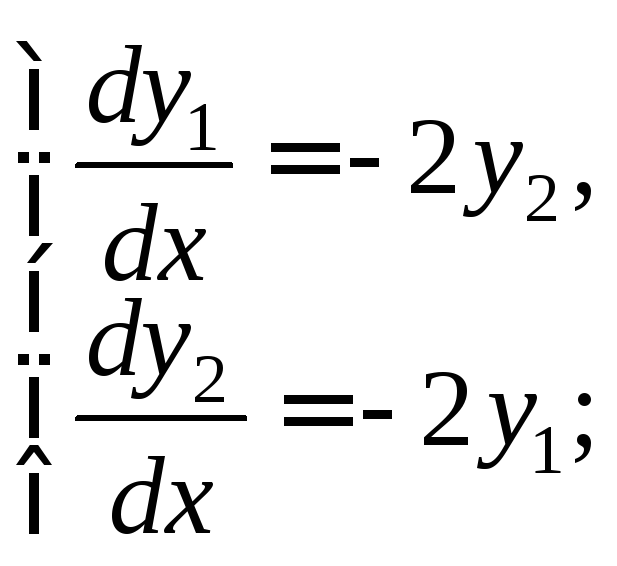 2)
2)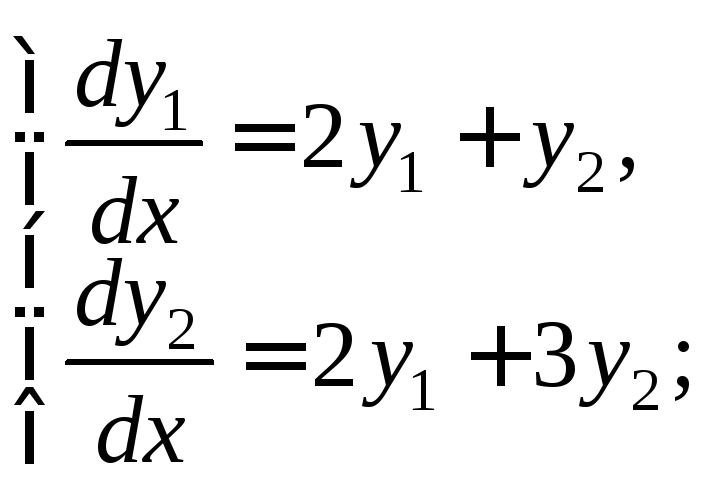
3)
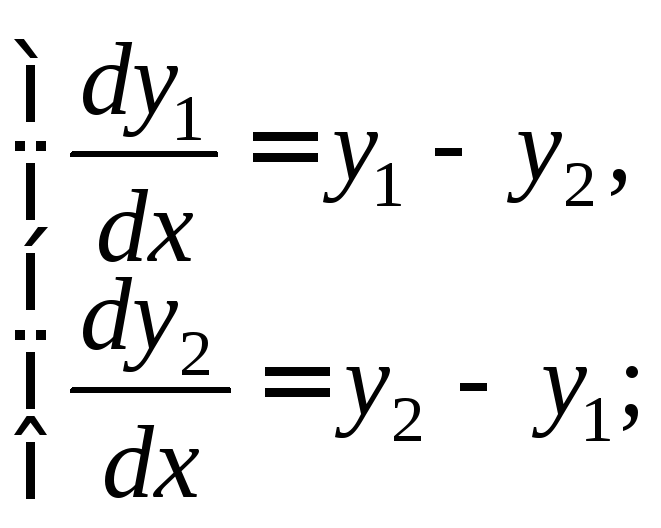 4)
4)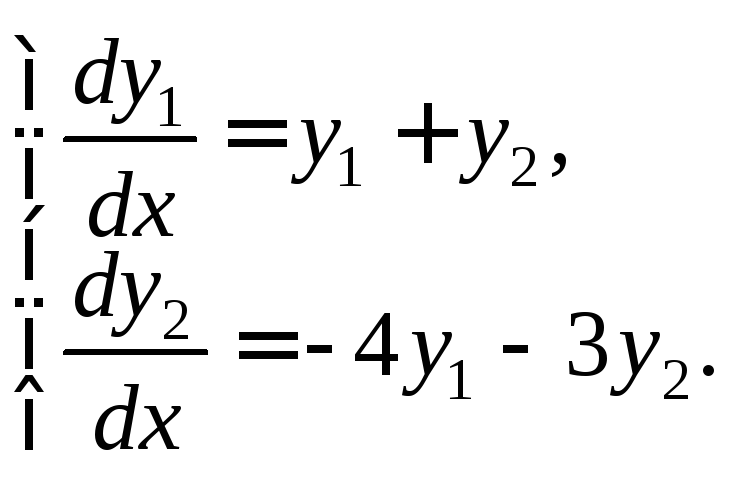
1.2.Решите задачу Коши:
1)
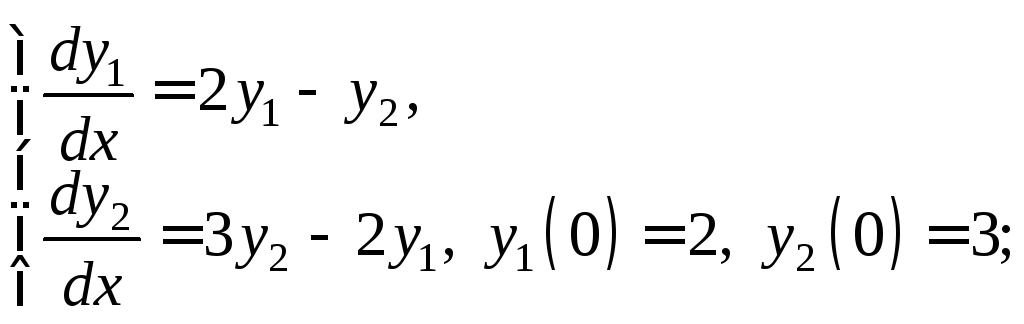
2)
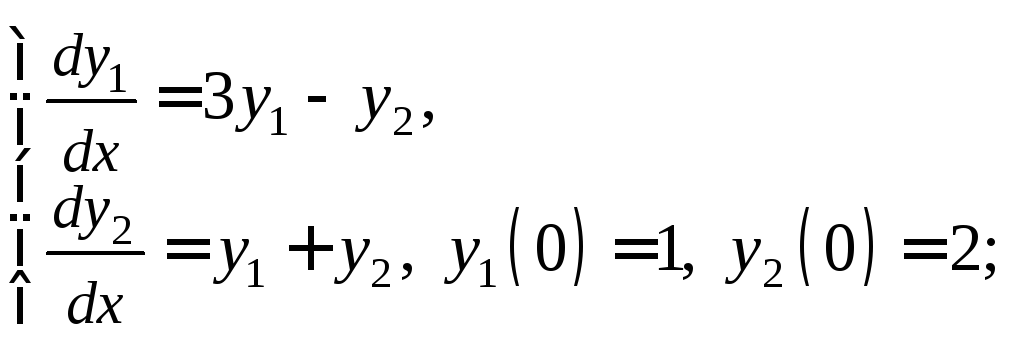
3)
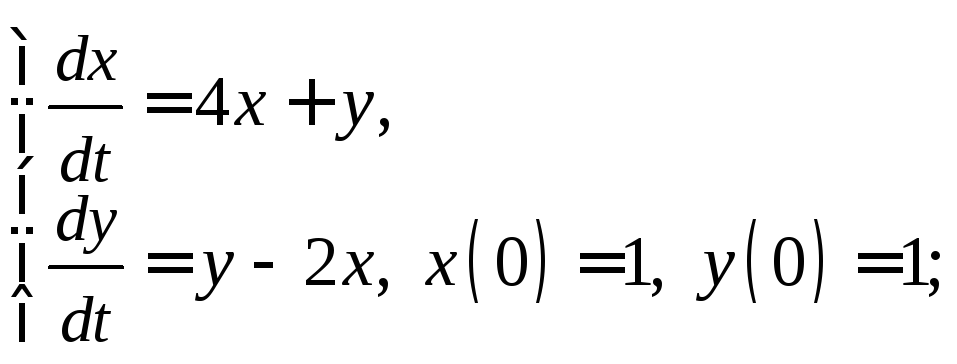
4)
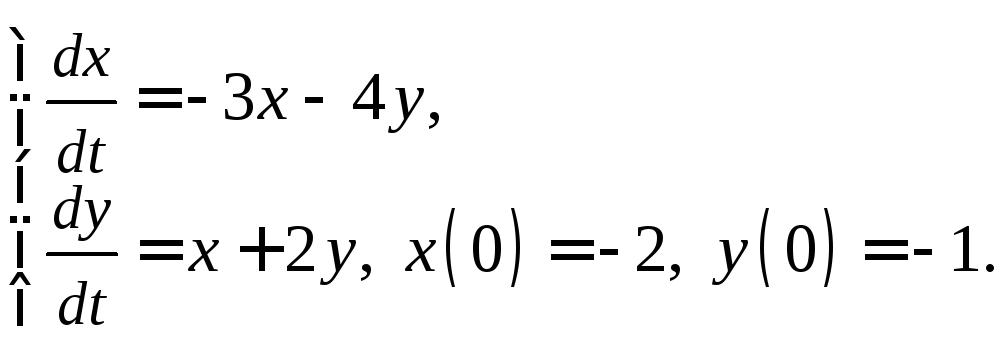
II уровень
2.1.Решите систему:
1)
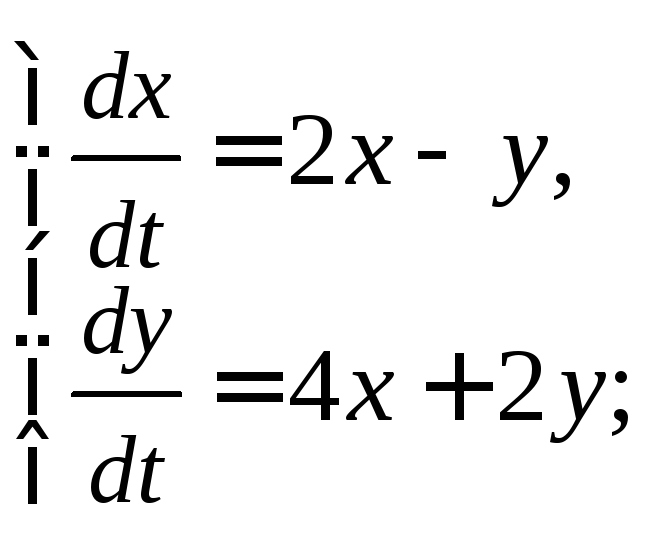 2)
2)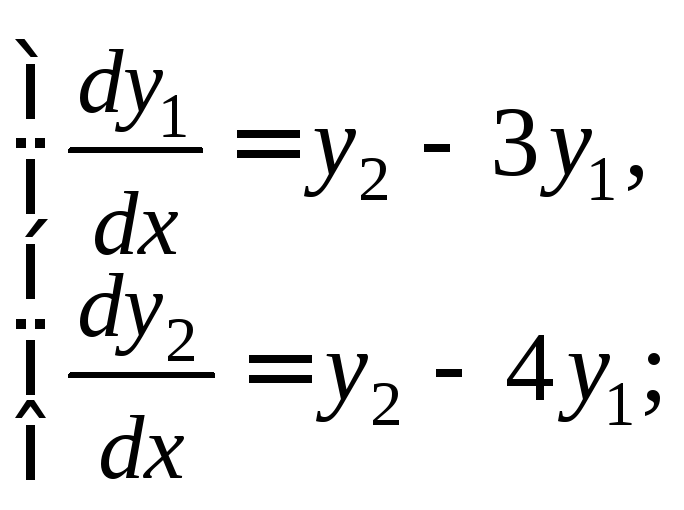
3)
 4)
4)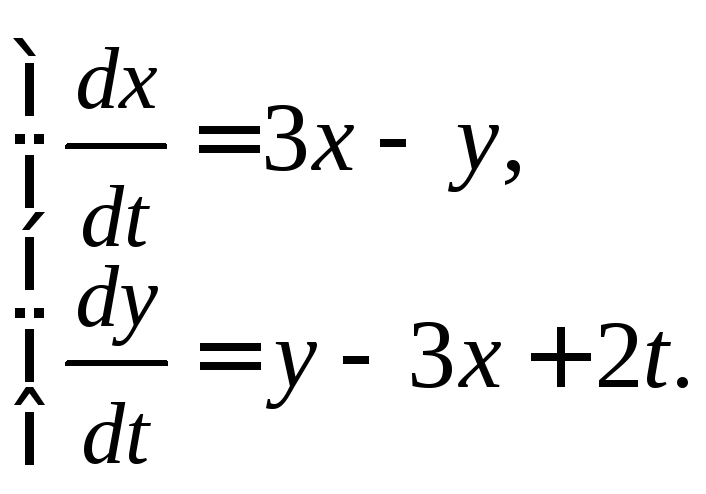
2.2.Решите задачу Коши:
1)
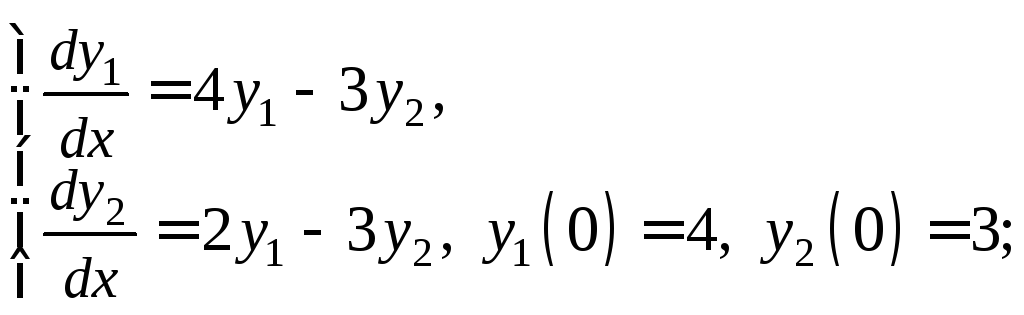
2)
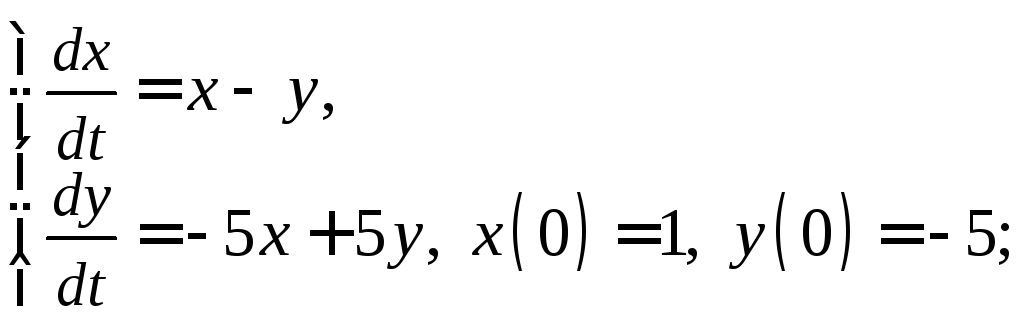
3)
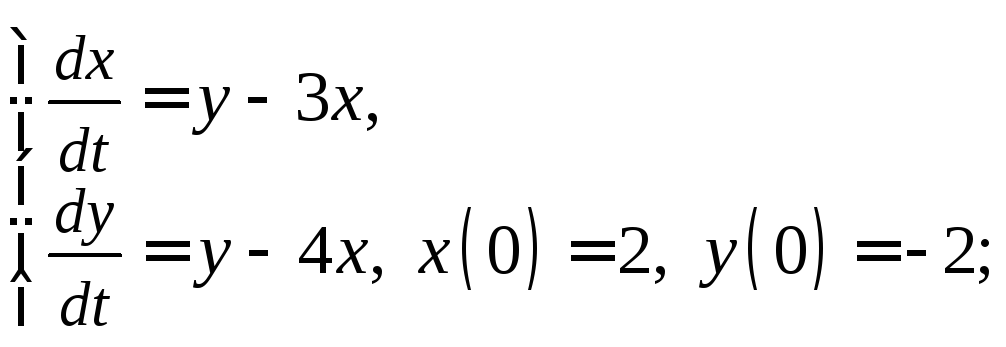
4)
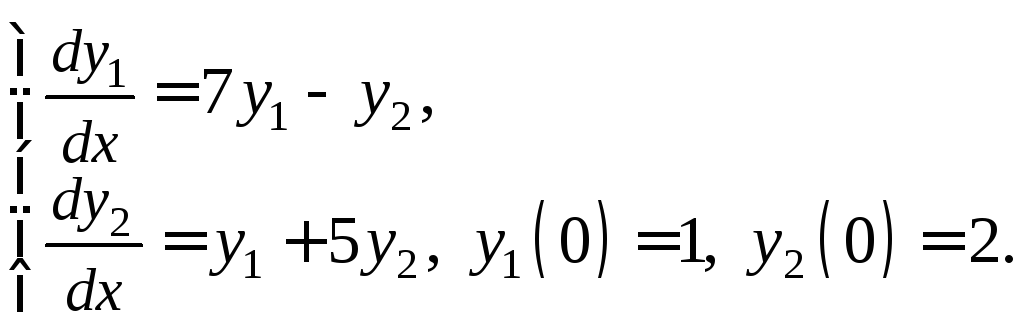
III уровень
3.1.Найдите частное решение системы дифференциальных уравнений:
1)
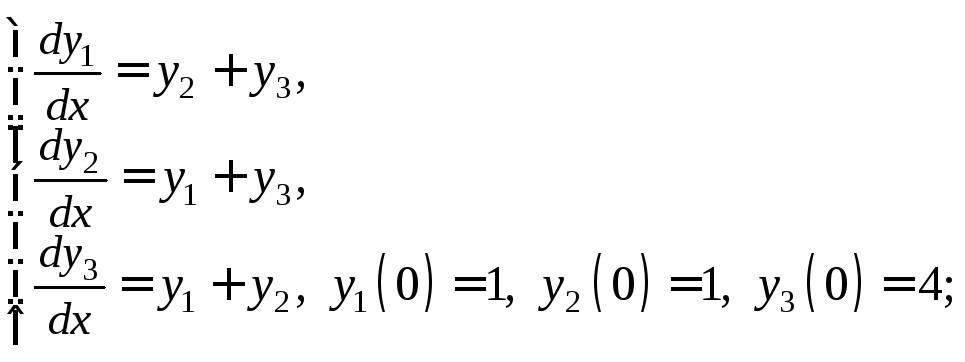
2)
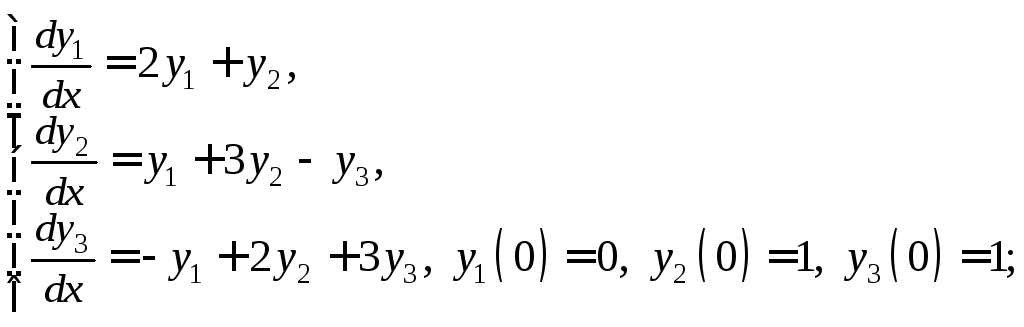
3)
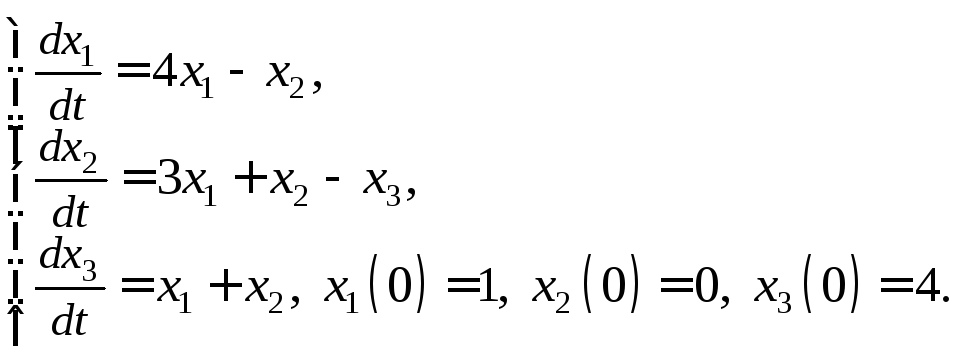
3.2.Решите систему дифференциальных уравнений методом интегрируемых комбинаций:
1)
 2)
2)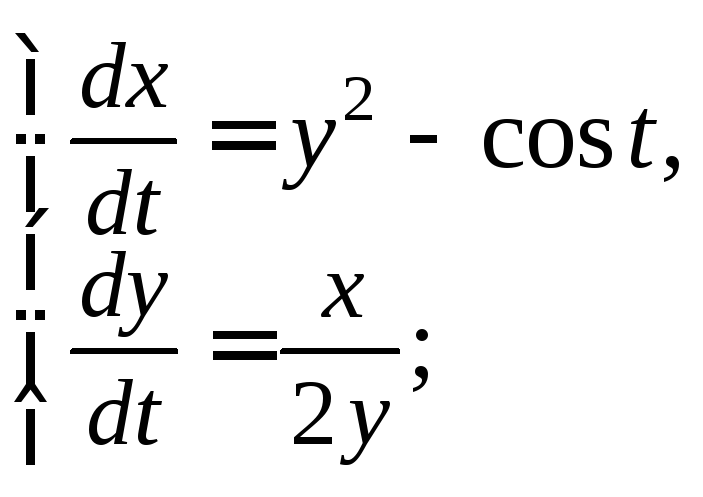
3)
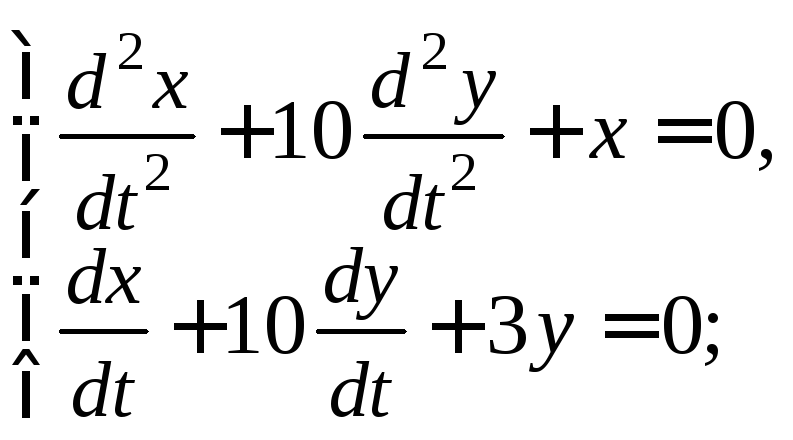 4)
4)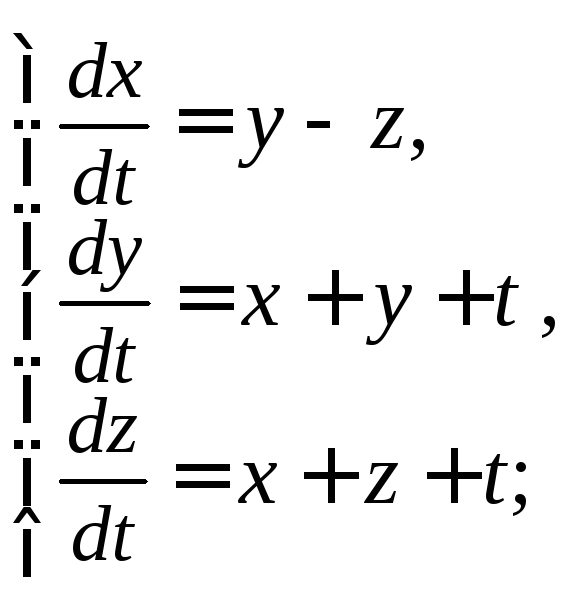
5)
![]()
6)
![]()
7)
![]()
Содержание
|
Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
|
3 |
|
19. Неопределенный интеграл. . . . . . . . . . . . . . . . . . . . . . . . . |
5 |
|
19.1. Свойства неопределенного интеграла. Таблица основных интегралов . . . . . . . . . . . . . . . . . . . . . . . . . . |
5 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
10 |
|
19.2. Методы вычисления неопределенного интеграла . . . |
13 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
17 |
|
19.3. Интегрирование некоторых выражений, содержащих квадратный
трехчлен
|
19 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
24 |
|
19.4. Метод интегрирования по частям . . . . . . . . . . . . . . . . |
25 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
32 |
|
19.5. Рациональные функции. Интегрирование простейших дробей . . . . . . . . . . . . . . . . . . . . . . . . . . . |
35 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
47 |
|
19.6. Интегрирование тригонометрических выражений . . . |
48 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
61 |
|
19.7. Интегрирование иррациональных функций . . . . . . . . |
64 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
71 |
|
19.8. Интегралы от дифференциальных биномов . . . . . . . . |
74 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
|
81 |
|
20. Определенный интеграл . . . . . . . . . . . . . . . . . . . . . . . . . . . |
83 |
|
20.1. Понятие определенного интеграла и его свойства . . . |
83 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
89 |
|
20.2. Формула Ньютона-Лейбница. Методы интегрирования по частям и замены переменной . . . . . . . . . . . . . . . . . |
91 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
99 |
|
20.3. Геометрические и физические приложения определенного интеграла . . . . . . . . . . . . . . . . . . . . . . . |
103 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
129 |
|
21. Несобственные интегралы. . . . . . . . . . . . . . . . . . . . . . . . . |
134 |
|
21.1. Несобственный интеграл первого рода . . . . . . . . . . . |
134 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
149 |
|
21.2. Несобственный интеграл второго рода . . . . . . . . . . . |
152 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
|
160 |
|
22. Дифференциальные уравнения . . . . . . . . . . . . . . . . . . . . . |
163 |
|
22.1. Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
163 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
170 |
|
22.2. Однородные дифференциальные уравнения. Уравнения, сводящиеся к однородным . . . . . . . . . . . |
172 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
180 |
|
22.3. Линейные уравнения. Уравнение Бернулли . . . . . . . |
181 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
189 |
|
22.4. Уравнения в полных дифференциалах . . . . . . . . . . . . |
191 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
195 |
|
22.5. Понятие дифференциальных уравнений высших порядков. Дифференциальные уравнения, допускающие понижение порядка . . . . . . . . . . . . . . . |
196 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
203 |
|
22.6. Линейные однородные дифференциальные уравнения высших порядков . . . . . . . . . . . . . . . . . . . . |
205 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
209 |
|
22.7. Линейные неоднородные дифференциальные уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
211 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
231 |
|
22.8. Системы дифференциальных уравнений . . . . . . . . . . |
232 |
|
22.9. Системы линейных однородных дифференциальных уравнений с постоянными коэффициентами . . . . . . . |
238 |
|
Задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
242 |
