22.9. Системы линейных однородных

дифференциальных уравнений с постоянными

коэффициентами

Система дифференциальных уравнений вида

(22.78)

где – числа, называетсясистемой линейных однородных дифференциальных уравнений с постоянными коэффициентами. Решение системы (22.78) ищут в виде

(22.79)

где – постоянные, которые подбираются по системе (22.78). Подставляя эти функции в систему (22.78), получаем системуnалгебраических уравнений сnнеизвестными

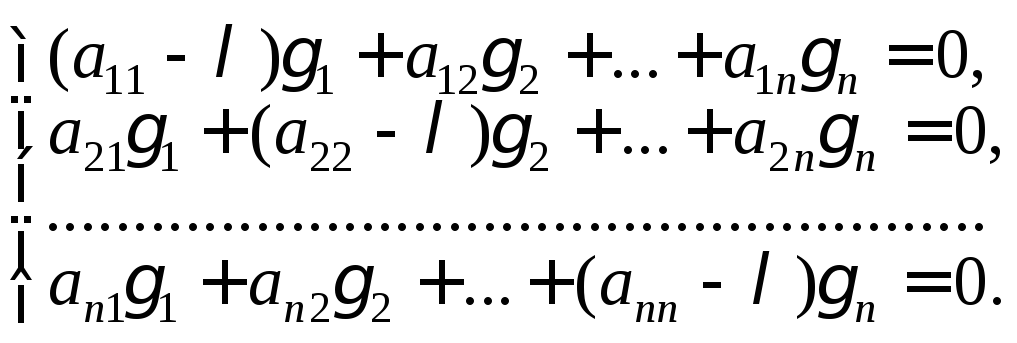(22.80)

Чтобы система (22.80) имела ненулевое решение, необходимо и достаточно, чтобы ее определитель был равен нулю:

(22.81)

Уравнение (22.81) называется характеристическим уравнениемсистемы (22.78). Оно имеетnкорней, вид которых определяет решение системы (22.78).

Правило нахождения общего решения системы

линейных однородных уравнений

1. Любому простому действительному корню характеристического уравнения (22.81) соответствует решение

где коэффициенты определяют из системы (22.80) при найденномт. е.

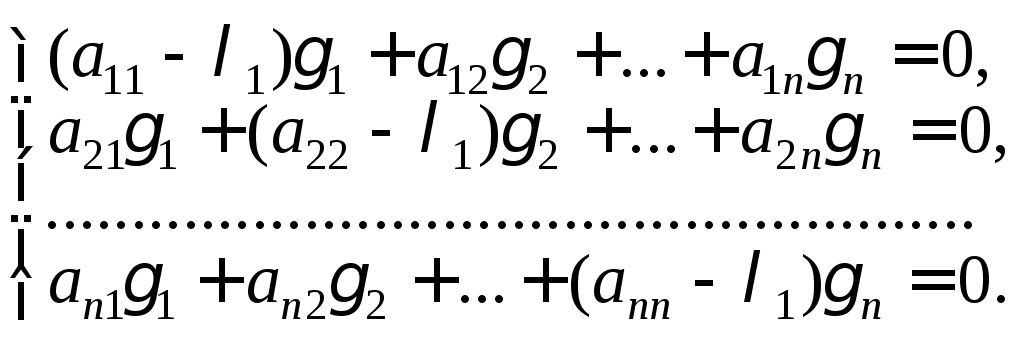(22.82)

Тогда общее решение системы (22.78) записывают в виде

где – произвольные постоянные.

2. Каждому комплексному корню и ему сопряженномусоответствуют два линейно-независимых действительных решения. Для построения этих решений находим комплексное решение по формуле (22.79) для корнякак и в случае 1, и выделяем действительную и мнимую части этого решения (кореньуже не рассматриваем, так как новых решений системы (22.78) он не дает).

3. Если – корень кратностиk, то решение, соответствующее этому корню, ищут в виде

(22.83)

где – многочлен с неопределенными коэффициентами степени

Чтобы найти коэффициенты многочленов подставляем решение (22.83) в систему (22.78) и приравниваем коэффициенты подобных членов в левой и правой частях уравнений. Выразив все коэффициенты через любые k, полагаем по очереди один из них равным единице, а остальные равными нулю.

Пример 1. Решить систему однородных дифференциальных уравнений с постоянными коэффициентами:

1) 2)

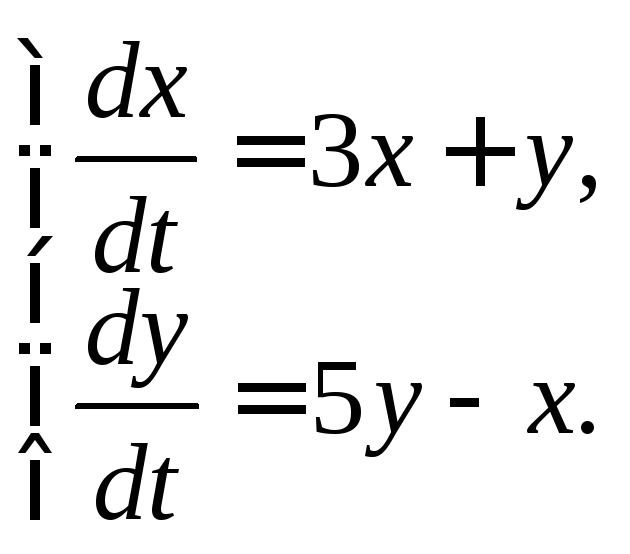
Решение. 1) Характеристическое уравнение системы имеет вид:

Вычисляя определитель, получаем откуда– простые действительные корни. Частные решения системы ищем в виде

При система (22.82) имеет вид:

Эта система имеет бесконечное множество решений. Для определенности положим тогдаПолучаем частные решения:

При система (22.82) принимает вид:

Положим тогда

Значит, корню соответствуют частные решения:

Общее решение исходной системы запишется в виде

2) Характеристическое уравнение системы

которое приобретает вид илиУравнение имеет двукратный кореньЕму соответствует решение вида

Продифференцируем функции x(t) и y(t) и подставим в исходную систему:

Сокращаем на и группируем. Получаем систему для коэффициентов

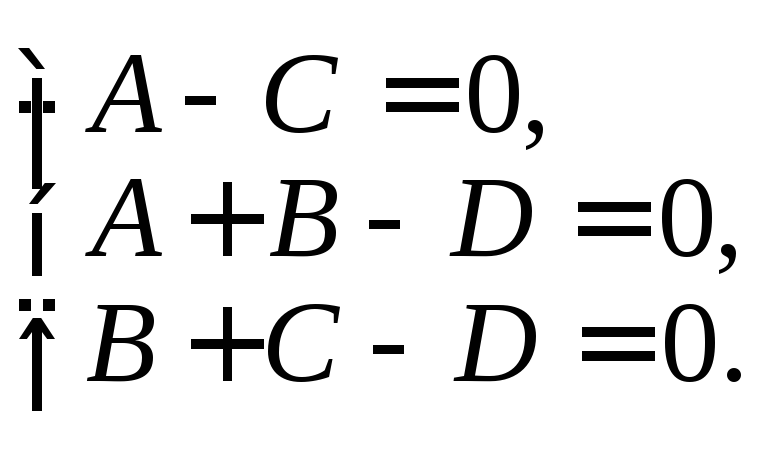
Так как кратность корня равна двум (k = 2), то выразим все коэффициенты последней системы через любые два, например, через A и B:

Полагая находимПолагаянаходим

Получаем два линейно-независимых частных решения:

и

Общее решение исходной системы имеет вид:

Пример 2. Найти частное решение системы

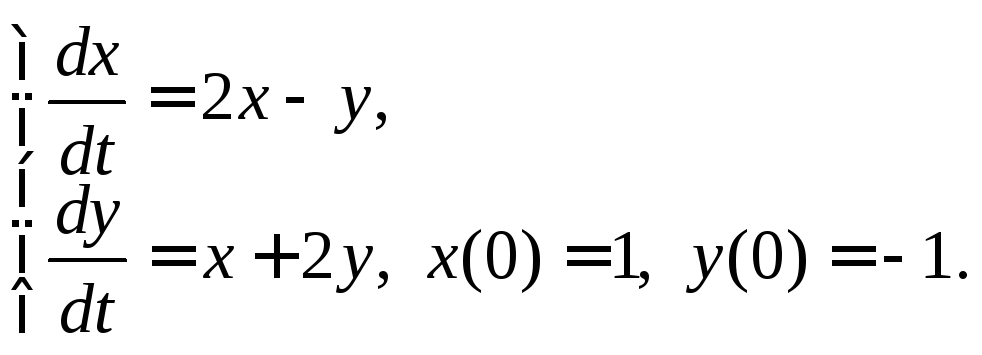
Решение. Характеристическое уравнение системы

т. е.

Оно имеет корни Для корнясоставляем систему (22.82):

Полагаем тогда

Частное комплексное решение системы:

Выделяем в полученных функциях действительные (Re) и мнимые (Im) части.

Поскольку то

тогда

Сопряженный корень новых линейно-независимых решений не дает, поэтому не рассматривается. Таким образом, общее решение исходной системы:

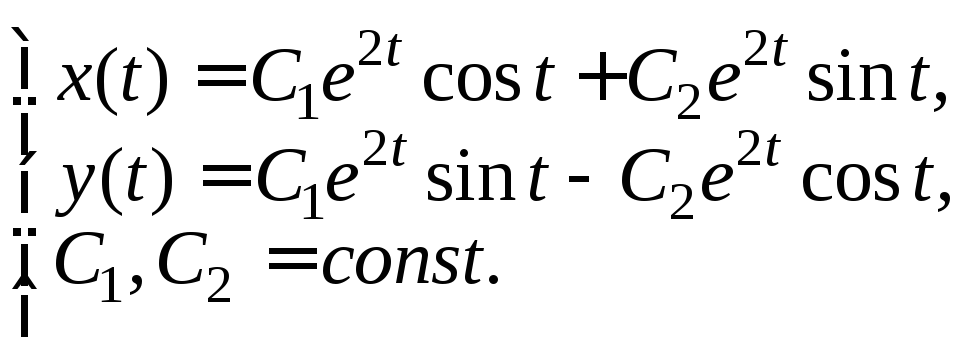
Найдем частное решение для заданных начальных условий. Получаем:

откуда находим

Искомое частное решение системы:

Задания