
- •20. Определенный интеграл
- •20.1. Понятие определенного интеграла и его свойства
- •I уровень
- •II уровень
- •III уровень
- •20.2. Формула Ньютона-Лейбница. Методы
- •I уровень
- •2. Длина дуги кривой
- •3. Объем тела
- •4. Объем и площадь поверхности тела вращения
- •5. Физические приложения определенного интеграла
- •I уровень
- •II уровень
- •III уровень
I уровень
1.1.Составьте интегральные суммы и, перейдя к пределу, найдите интеграл. При составлении интегральных сумм значение функции вычислите:
1) в правом конце каждого частичного отрезка;
2) в левом конце каждого частичного отрезка:
1)
 2)
2)![]() 3)
3)![]()
У к а з а н и я. Воспользуйтесь равенствами:
1. ![]()
2. ![]()
3. Сумма
n
членов геометрической прогрессии равна
![]()
II уровень
2.1.Сравните интегралы:
1)
![]() и
и![]() 2)
2) и
и
3)
 и
и 4)
4)![]() и
и![]()
5)
![]() и
и![]() 6)
6)![]() и
и![]()
7)
 и
и![]() 8)
8) и
и
2.2.Вычислите интеграл, используя свойства определенного интеграла:
1)
 2)
2) 3)
3)
4)
 5)
5) 6)
6)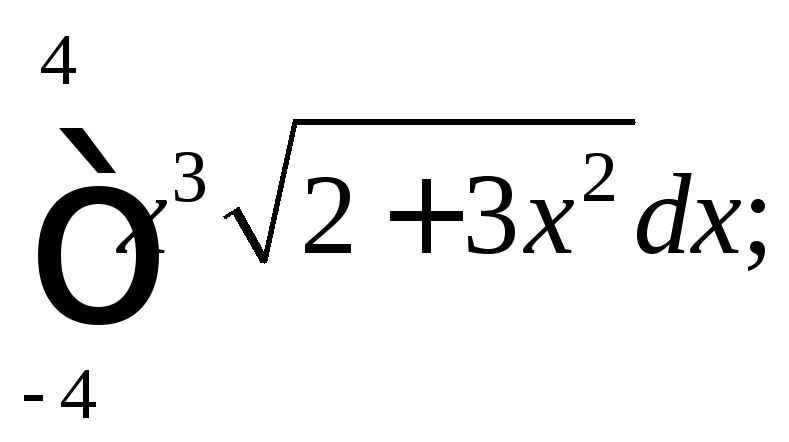
7)
 8)
8) 9)
9)
III уровень
3.1.Докажите неравенство:
1)
 2)
2)
3)
 4)
4)
3.2.Оцените интеграл:
1)
 2)
2)
3)
 4)
4)
20.2. Формула Ньютона-Лейбница. Методы
интегрирования по частям и замены переменной
Если функция f (x) непрерывна на отрезке [a; b] иF(x) – ее первообразная на этом отрезке, то
 (20.3)
(20.3)
Формула (20.3) называется формулой Ньютона-Лейбница.
Интегрирование по частям
Пусть u(x) иv(x) – непрерывные функции, которые имеют непрерывные производные на отрезке [a; b]. Тогда справедлива формула интегрирования по частям:
 (20.4)
(20.4)
Замена переменной в определенном интеграле
Пусть f (x)
– непрерывная на отрезке [a; b]
функция, а функция![]() и ее производная
и ее производная![]() непрерывны на отрезке
непрерывны на отрезке![]() где
где![]()
![]() Тогда справедлива формула
Тогда справедлива формула
 (20.5)
(20.5)
Вместе с заменой переменной в определенном интеграле заменяются пределы интегрирования.
Пример 1. Вычислить интеграл:
1)
 2)
2)
3)
 4)
4)
Решение. 1) Применим формулу Ньютона-Лейбница (20.3):

2)
Подынтегральная функция
![]() является четной. Поэтому
является четной. Поэтому

3) Подынтегральная функция является неправильной рациональной дробью. Выделим целую часть, разделив ее числитель на знаменатель по правилу деления многочленов:

Тогда

![]()
![]()
4) Подынтегральная функция является правильной рациональной дробью. Разложим ее на сумму простейших дробей:
![]()
Найдем коэффициенты A, B, C из равенства
![]()
Полагая
![]() получаем
получаем![]() При
При![]() получаем
получаем![]() Полагая
Полагая![]() получаем
получаем![]() Далее находим:
Далее находим:![]()
![]() т. е.
т. е.![]()
Тогда

![]()
Пример 2. Вычислить интеграл, используя формулу интегрирования по частям:
1)
 2)
2)
3)
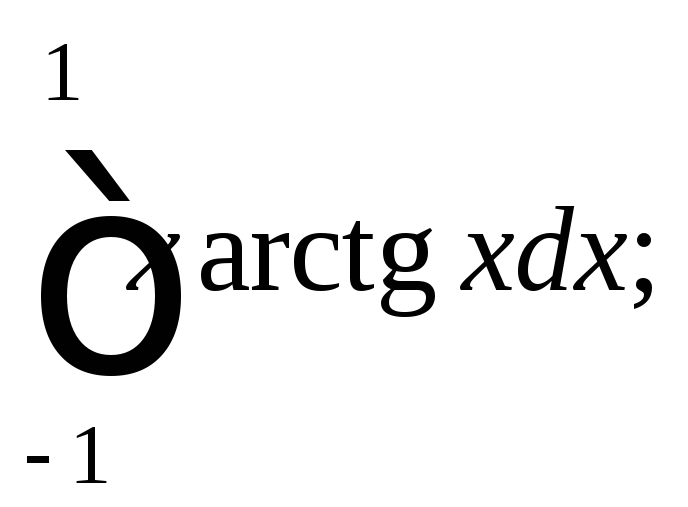 4)
4)

Решение. 1) По формуле (20.4) имеем:



2) Используем формулу (20.4):


3) Подынтегральная функция является четной, поэтому
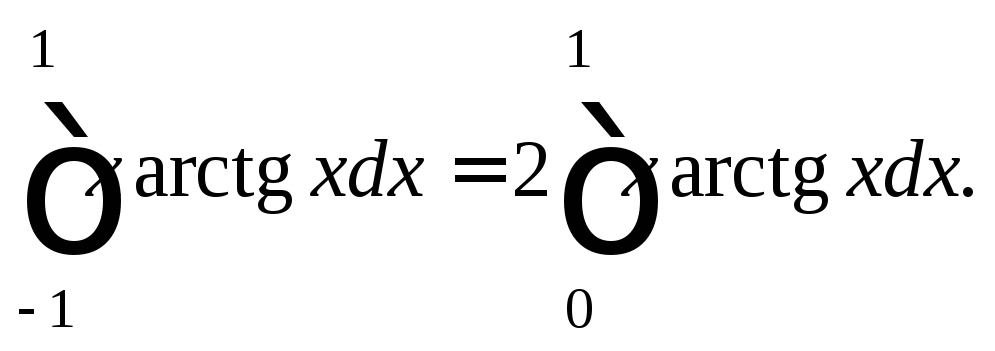
Применим
формулу (20.4) интегрирования по частям.
Пусть
![]()
![]()
![]()
![]()
Получим:

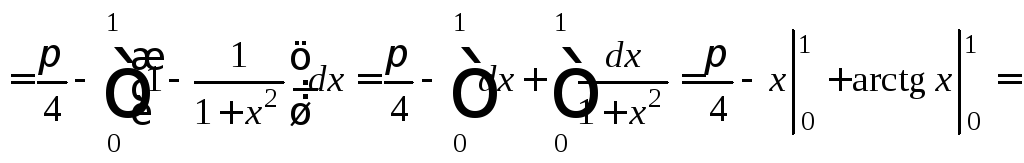
![]()
4) Используем формулу (20.4) интегрирования по частям дважды:




Таким образом, получили равенство

Из него находим:


Пример 3. Вычислить определенный интеграл, используя формулу замены переменной:
1)
 2)
2) 3)
3)
4)
 5)
5)
 6)
6)
Решение.
1) Сделаем подстановку
![]()
![]() тогда
тогда![]() Определим новые пределы интегрирования.
Для этого в равенство замены переменной
поочередно подставим
Определим новые пределы интегрирования.
Для этого в равенство замены переменной
поочередно подставим![]() (заданный нижний предел интегрирования)
и
(заданный нижний предел интегрирования)
и![]() (заданный верхний предел): если
(заданный верхний предел): если![]() то
то![]()
![]() если
если![]() то
то![]()
![]()
Используем формулу (20.5) замены переменной в определенном интеграле:

Получили интеграл от неправильной рациональной дроби. Выделим целую часть в подынтегральном выражении:

![]()
![]()
2)
1-й способ.
Используем метод подстановки. Положим
![]() тогда
тогда![]()
Найдем
новые пределы интегрирования: если
![]() то
то![]() если
если![]() то
то![]()
Следовательно,


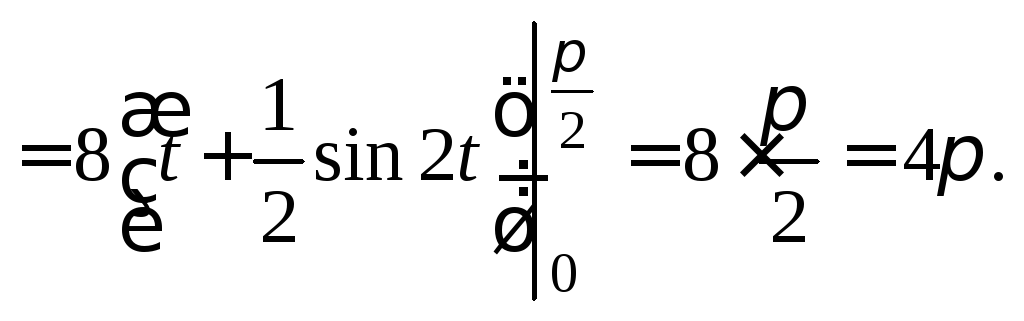
2-й способ. Используем формулу (20.4) интегрирования по частям.
Положим
![]()
![]() тогда
тогда![]()
![]()
Получаем:



Найдем искомый интеграл из полученного равенства

Выражаем:

3)
Применим подстановку
![]()
Тогда
![]() т. е.
т. е.![]()
![]()
![]()
![]()
![]()
Таким образом, подынтегральное выражение примет вид:
![]()
Определим
новые пределы интегрирования: если
![]() то
то![]() т. е.
т. е.![]()
![]()
![]()
![]() Находим
Находим![]()
если
![]() то
то![]() т. е.
т. е.![]()
![]()
![]()
![]() Находим
Находим![]()
Получаем:

4) В подкоренном выражении выделим полный квадрат:
![]()
Применим
подстановку
![]()
![]()
![]()
Определим
новые пределы интегрирования: если
![]() то
то
![]()
![]()
![]() если
если![]() то
то![]()
![]()
![]()
Получаем:
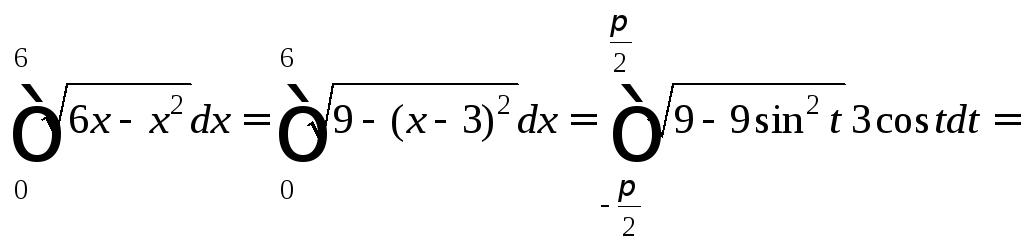

![]()
5)
1-й способ.
Используем метод замены переменной.
Положим
![]() Тогда
Тогда![]()
Находим
новые пределы интегрирования, используя
равенство замены переменной: если
![]() то
то![]() если
если![]() то
то![]()
Получим:

2-й способ. Используем метод поднесения под знак дифференциала:

![]()
Заметим, что в случае использования метода поднесения под знак дифференциала не нужно изменять пределы интегрирования, а поэтому, как правило, он является более рациональным.
6) Применим подстановку:
![]() тогда
тогда
![]()
Выразим переменную x через t:
![]()
![]()
![]()
![]()
![]()
![]()
Определим
новые пределы интегрирования: если
![]() то
то![]() если
если![]() то
то![]()
Используя формулу (20.5) замены переменной в определенном интеграле, получаем:

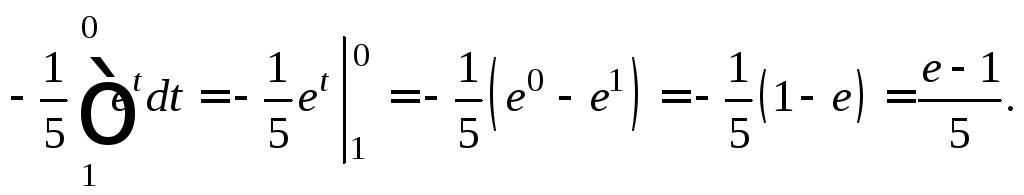
Задания
