Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт информационных технологий БГУИР

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТМ / Теория / TM_Lectures.pdf

Скачиваний:

170

Добавлен:

24.02.2016

Размер:

6.53 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 745 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

3)непрерывные по времени и дискретные по множеству (рис. 1.3,в);

4)непрерывные по множеству и дискретные по времени (рис. 1.3,г).

1.2. Периодические сигналы

Представление периодического сигнала суммой гармонических составляющих осуществляется с помощью разложения в ряд Фурье функции (1.1), которая является временным представлением сигнала. Если функция f(t)задана на интервале времени t1≤ t≤ t2 и повторяется с периодом T=2π/Ω1 = t2 - t1, то тригонометрическая форма ряда Фурье для нее может быть записана следующим образом:

			a0		∞
f (t) =			a0	+ ∑(ak cos kΩ1t + bk sin kΩ1t) =
f (t) =				+ ∑(ak cos kΩ1t + bk sin kΩ1t) =
			2		k	=1
			∞		k	=1
	A0		∞					), k = 1, 2, ….
=	A0	+	∑		A	cos(kΩ t −ψ	k		(1.5)
=		+			A	cos(kΩ t −ψ			(1.5)
	2				k	1
	2		k =1
			k =1

Амплитуды косинусоидальных и синусоидальных членов в разложении (1.5) определяются выражениями:

					2 T						(1.6)

ak = T ∫							f (t) cos(kΩ1t)dt ;
ak = T ∫							f (t) cos(kΩ1t)dt ;
					0
					2 T
bk =						∫ f (t)sin(kΩ1t)dt .					(1.7)
bk =				T		∫ f (t)sin(kΩ1t)dt .					(1.7)
					0
Слагаемое
	a	0			A				1 T
		0	=		0		=			∫ f (t)dt	(1.8)
2			=		2		=	T		∫ f (t)dt	(1.8)
2					2			T		0
										0

является постоянной составляющей сигнала, которая, как это следует из (1.8), равна среднему значению функции f(t)за период.

Амплитуда Ak и фаза ψk

k-й гармоники, как это следует из (1.5), связа-

ны с величинами ak и bk соотношениями:

A =

+ b2 ,

= A cosψ

= A sin ψ

;

(1.9)

ψk

= arctg(bk

ak ) .

(1.10)

Весьма удобной является комплексная форма записи ряда Фурье, к которой легко перейти, если в разложении (1.5) выразить тригонометрические функции через показательные, воспользовавшись известными формулами:

cos kΩ t =

(e jkΩ1t + e− jkΩ1t ) ;

sin kΩ t =

(e jkΩ1t

− e− jkΩ1t ) .

2 j

В результате получим

∞

f (t) =

∑ (A&k e jkΩ1t

+ Ak e− jkΩ1t ) ,

(1.11)

2 k =1

где A&

и b

соотношениями

Ak – комплексные амплитуды, связанные с a

= Ak e

− jψk

= ak − jbk

(1.12)

= Ak e jψk

= ak + jbk .

(1.13)

•

Таким образом, комплексные амплитуды Ak

являются комплексно-

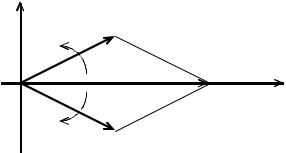
сопряженными величинами. Действительно, каждое слагаемое первого ряда в выражении (1.11) можно представить как вектор на комплексной плоскости

(рис. 1.4), вращающийся с частотой kΩ1 (т.е. в положительном направлении отсчета углов – против направления движения часовой стрелки). Каждое слагаемое второго ряда – вектор, вращающийся в обратном направлении.

j	•
kΩ1	A

– kΩ *

1 A

Рис. 1.4. Векторная диаграмма комплексно-сопряженных величин

•	*	– комплексно-сопряженные величины, то сумма век-
Так как Ak	и Ak	– комплексно-сопряженные величины, то сумма век-

торов в любой момент времени дает вектор, направленный по вещественной оси, т.е. k-ю гармоническую составляющую вещественной функции времени

f(t). Отрицательная частота – kΩ1 только указывает направление вращения вектора.

•

Комплексная амплитуда Ak определяется по выражению

•			1	T		Ω1	T
				∫	f (t)e− jkΩ1t dt =		∫ f (t)e− jkΩ1t dt .
Ak	=							(1.14)
		T
				0		2π	0

При k = 0

A			1 T		Ω	T	a	0
0	=			∫ f (t)dt =	1	∫ f (t)dt =			.	(1.15)
2		T					2
				0	2π	0

Тогда выражение (1.11) можно переписать в виде

	1 k=∞ •		jkΩt
f (t) =		∑ Ak e	1 .	(1.16)

	2k=−∞

При такой записи ряда Фурье периодический сигнал заменяется суммой простых гармонических колебаний как с положительными частотами (k > 0), так и с отрицательными (k < 0). Конечно, отрицательные частоты не имеют здесь физического смысла, а являются формальным следствием произведенного математического преобразования.

1.3. Спектры периодических сигналов

инеобходимая ширина полосы частот

1.3.1.Дискретный спектр. Представить сигнал с заданным периодом T рядом Фурье – это значит найти амплитуды и начальные фазы всех его гармонических составляющих. Совокупность амплитуд называют спектром амплитуд, а совокупность начальных фаз – спектром фаз. Во многих частных случаях достаточно рассчитать только спектр амплитуд сигнала, который для краткости назовем просто спектром.

Определим спектр периодической последовательности прямоугольных

импульсов (рис. 1.5) длительностью τ и с периодом T. Напряжение такой формы действует в каналах связи и часто рассматривается как основной периодический сигнал при исследовании передачи информации по линии связи.

u(t)

t1 0 t2

T τ

Рис. 1.5. Периодическая последовательность прямоугольных импульсов

Для такого сигнала по формулам (1.6) – (1.8)

τ 2

∫

Udt = U

;

−τ 2

τ 2

U cos kΩ1tdt =

sin k

π;

∫

kπ

−τ 2

bk = 0, т.е.

ψk

= 0 или π

Следовательно, напряжение можно представить рядом Фурье

u(t) = U (

(sin

πcos Ω t + 1 sin 2

πcos 2Ω t +

∞

sin kΩ τ 2

sin 3

πcos 3Ω1t + K)) = U

(1 + ∑2

cos kΩ1t) .

(1.17)

kΩ1 τ

k =1

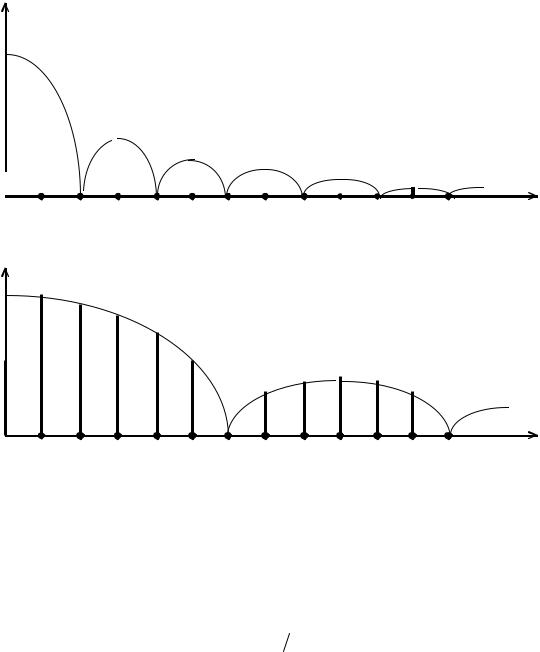
Спектр амплитуд сигнала изображают в виде спектральных линий, длины которых пропорциональны амплитудам гармоник (рис. 1.6). Такой спектр называют линейчатым или дискретным. Спектр фаз ψk также линейчатый,

причем в рассматриваемом частном случае ψk может иметь только два значе-

ния: 0 или π.

Непрерывная кривая, соединяющая концы линий спектра и показанная на рис. 1.5 пунктиром, носит название огибающей спектра амплитуд, которая определяется уравнением

A(Ω) =	2Uτ	sin(Ωτ 2)	,	(1.18)
	T	Ωτ 2

где Ω = kΩ1 для k-й гармоники.

τ=

2π

4π

6π

8π

12π

10π

Ω

Ω1

2Ω1 3Ω14Ω1 5Ω1 6Ω1 7Ω1 8Ω1 9Ω1 10Ω1 11Ω1 12Ω1

τ= T

2π

4π

Ω

Ω1 2Ω1 3Ω1 4Ω15Ω1 6Ω17Ω1 8Ω1 9Ω110Ω111Ω112Ω1

Рис. 1.6. Спектры периодически повторяющихся прямоугольных импульсов при Q=2 и Q=6

Выражение для фазы гармоники можно записать в виде

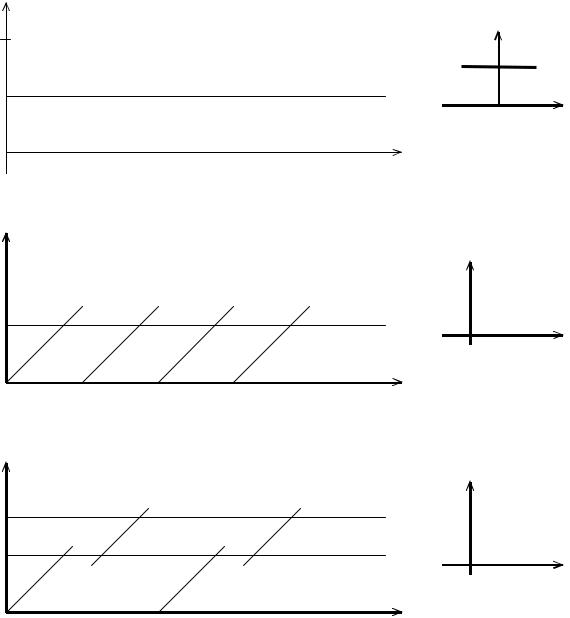
ψk = kΩ1(t1 + τ 2) + (k −1)π.

(1.19)

На рис. 1.7 приведены спектры фаз и их огибающие при различно выбранных началах отсчета времени. Наиболее простым получается спектр фаз

при t1 = −τ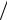2 .

Кроме того, из (1.17) и рис. 1.6 следует, что периодическую последовательность прямоугольных импульсов можно рассматривать как результат наложения друг на друга бесконечного количества гармоник с частотами, кратными основной частоте Ω1= 2π/T, а также постоянной составляющей. Амплитуды гармонических составляющих кратных скважности Q равны нулю (например, равны нулю амплитуды четных гармоник на рис. 1.6, где принято τ=T/2, и шестая, двенадцатая и т.д., где принято τ = T / 6).

ψk

f(t)

2π

-τ

2π

4π

6π

8π

Ω

ψk

2π

f(t)

2π

4π

6π

8π

Ω

ψk

f(t)

3π

2π

4π

6π

8π

3τ/2

Ω

Рис. 1.7. Спектры фаз при различных началах отсчета времени

С изменениями длительности импульса τ при том же периоде следования импульсов T или с изменением периода T при постоянной длительности τ спектр существенно преобразуется. Если длительность импульса растет, то увеличивается удельный вес постоянной составляющей и гармоник с небольшими порядковыми номерами, а удельный вес высших гармоник падает. Если, наоборот, уменьшить длительность импульса τ, то удельный вес гармоник с

небольшим порядковым номером уменьшается, а удельный вес высших гармоник растет.

При изменении не длительности импульсов τ, а периода их повторения T спектр амплитуд становится реже или гуще. Так, с увеличением периода T основная частота уменьшается (Ω1= 2π /T) и спектр становится гуще.

1.3.2. Практическая ширина спектра. Теоретически, как указывалось выше, для большинства периодических функций спектр неограничен, т.е. для передачи сигналов телемеханики без изменения формы необходимы бесконечно большая полоса пропускания канала связи и отсутствие амплитудных и фазовых искажений. Практически все каналы связи имеют ограниченную полосу пропускания, и форма сигналов при передаче по каналу изменяется даже при отсутствии в этой полосе амплитудных и фазовых искажений. Очевидно, важно передать ту часть спектра сигнала, которая содержит гармонические составляющие с относительно большими амплитудами. В связи с этим вводится понятие практической ширины спектра сигнала. Под практической шириной спектра сигнала понимается та область частот, в пределах которой лежат гармонические составляющие сигнала с амплитудами, превышающими наперед заданную величину.

Поскольку средняя мощность, выделяемая сигналом на активном сопротивлении, равном 1 Ом, складывается из мощностей, выделяемых на этом сопротивлении гармоническими составляющими,

	A2	∞	A2
Pñð =	0	+ ∑	k	,	(1.20)
Pñð =	4	+ ∑	2	,	(1.20)
	4	k =1	2

практическая ширина спектра с энергетической точки зрения может быть определена как область частот, в пределах которой сосредоточена подавляющая часть мощности сигнала.

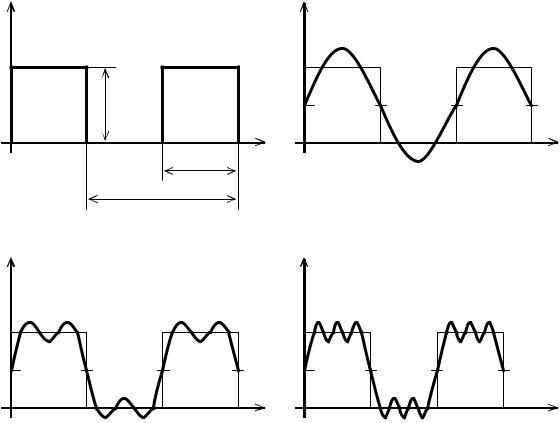
В качестве примера определим практическую ширину спектра периодической последовательности прямоугольных импульсов (рис. 1.8,а), если требуется учесть все гармонические составляющие сигнала, амплитуды которых более 0,2 от амплитуды первой гармоники. Число подлежащих учету гармоник k может быть получено из выражения

Ak = 2U π = 1 = 0,2 ,

A1 kπ 2U k

откуда k=5.

Таким образом, практическая ширина спектра в рассмотренном примере оказывается равной 5Ω1, в ней размещаются всего три гармоники (первая, третья и пятая) и постоянная составляющая.

Средняя мощность Pk5, выделяемая в активном сопротивлении, равном 1 Ом, перечисленными составляющими, равна

U 2

0,48 U 2 .

k 5

4 2

2 3π

2 5π

Средняя мощность, выделяемая в этом же сопротивлении всеми составляющими сигнала, будет

PkΣ = Pèìï Q = 0,5 U 2 .

Таким образом, (Pk 5 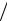PkΣ ) 100 = 96%, т.е. составляющие, входящие в

практический спектр, выделяют в активном сопротивлении 96 % всей мощности сигнала.

U(t)		U(t)
			A0+A1(t)
a		б
U
0	T/2	t 0	t
	T/2
T
U(t)		U(t)	A0+A1(t)+A3(t)+A5(t)
A0+A1(t)+A3(t)			A0+A1(t)+A3(t)+A5(t)
в		г

t 0

Рис. 1.8. Формы сигнала при ограничении спектра последовательности прямоугольных импульсов

Очевидно, расширение практического спектра данного сигнала (свыше 5Ω1) с энергетической точки зрения нецелесообразно.

Ограничение спектра сигнала оказывает также влияние на его форму. Для иллюстрации на рис. 1.8 показано изменение формы прямоугольных импульсов при сохранении в спектре только постоянной составляющей и первой

<<< < Предыдущая 1 2 3 45 / 745 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

•			1	T		Ω1	T
				∫	f (t)e− jkΩ1t dt =		∫ f (t)e− jkΩ1t dt .
Ak	=							(1.14)
		T
				0		2π	0

•			1	T		Ω1	T
				∫	f (t)e− jkΩ1t dt =		∫ f (t)e− jkΩ1t dt .
Ak	=							(1.14)
		T
				0		2π	0

•			1	T		Ω1	T
				∫	f (t)e− jkΩ1t dt =		∫ f (t)e− jkΩ1t dt .
Ak	=							(1.14)
		T
				0		2π	0