Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт информационных технологий БГУИР

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТМ / Теория / TM_Lectures.pdf

Скачиваний:

192

Добавлен:

24.02.2016

Размер:

6.53 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 7413 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Как видно из приведенных спектров, необходимая полоса частот в два раза шире, чем для видеоимпульсов, т.е.

∆ω=2π/τ или ∆F=2/τ,

а при ФМП на ∆ϕ = 180° и Q=2 несущая в спектре отсутствует.

При передаче дискретных сообщений используется не только двухпозиционная ФМП. Все шире применяются методы двукратной (четырехпозиционной) и трехкратной (восьмипозиционной) ФМП. Величины скачка фазы сигнала в этих случаях могут принять соответственно 4 и 8 значений. Для таких случаев также применимы полученные выше результаты. Спектр боковых полос, сохраняя одну и ту же форму, при изменении величины скачка будет изменять свою амплитуду.

Для более сложных случаев, когда чередуются скачки фазы разной величины, приведенные формулы несправедливы. Спектр может изменяться значительно.

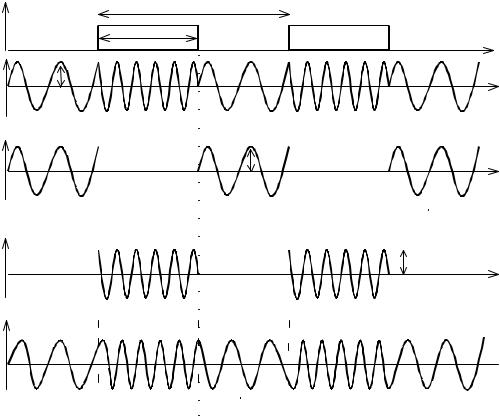
4.3. Частотная манипуляция (ЧМП)

При частотной манипуляции частота носителя под действием прямоугольного модулирующего сообщения принимает скачком два граничных

значения частоты ωmin и ωmax.

Временные диаграммы для ЧМП приведены на рис. 4.5,б.

C(t)

UЧМП

UАМП1

Fmin

Fmax

Fmin

Fmax

Fmin

UАМП2

Fmax

UЧМП

д t

Fmin	Fmax	Fmin	Fmax	Fmin

Рис. 4.5. Частотная манипуляция

Ω=2π/T

Такой сигнал можно представить как сумму двух сигналов с амплитудной манипуляцией (рис. 4.5, в, г), т.е. полученных от двух генераторов с амплитудной манипуляцией. В моменты переключений колебания на одной частоте прекращаются и возникают на другой частоте. Так как фазы в эти моменты могут быть различны, то фаза результирующего сигнала (рис. 4.5,б) изменяется скачком. Спектр сигнала на рис. 4.5,б также составляется из спектров двух сигналов UАМП1 и UАМП2 на рис. 4.5, в,г. Результирующий спектр представлен на рис. 4.6.

| Ak |

		Q=2
	Ω Ω		Ω Ω		ω
	ωmin		ωmin


	2Ωmax		2Ωmax
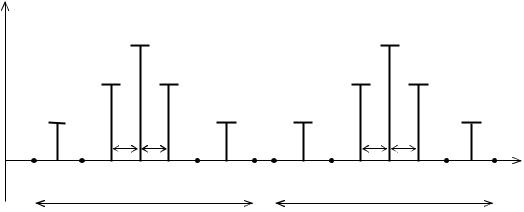
	Рис. 4.6. Спектр ЧМП-сигнала с разрывом фазы
Необходимая ширина спектра, очевидно, равна
		∆ω=(ωmax-ωmin)2Ωmax,		(4.11)

т.е. больше, чем при АМП, на величину ωmin–ωmax.

В системах телемеханики такой метод получения сигналов с ЧМП практически не применяется.

Обычно для ЧМП изменяют скачкообразно один из параметров генератора несущих колебаний. При таком изменении параметра частота генерируемых колебаний также изменяется скачком, но без разрыва фазы (рис. 4.5,д). Отсутствие скачкообразного изменения фазы существенно сказывается на спектре сигнала с ЧМП. Найдём этот спектр, предполагая, что модулирующим сигналом C(t)является последовательность прямоугольных импульсов (рис. 4.5,а) с периодом T=2π/Ώ.

Тогда ЧМП-сигнал можно записать в виде

UЧМП(t) =U sin(ω1t + ∆ω∫( 2C(t) −1)dt ),

(4.12)

где U – амплитуда носителя; ∆ω=2π∆f – девиация частоты, т.е. величина максимального отклонения мгновенной частоты от несущей.

После тригонометрического преобразования получим

U×ÌÏ (t) = U(sinω1t cosψ + cosω1t sinψ),

(4.13)

где ψ = ∆ω∫(2C(t) −1)dt – изменение фазы в результате частотной манипуля-

ции.

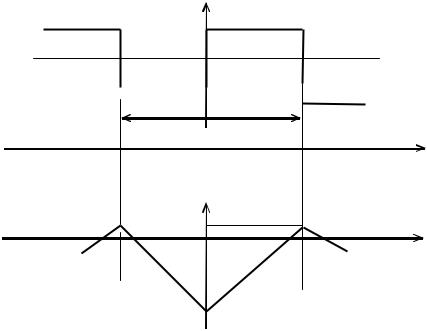
График изменения фазы приведён на рис. 4.7,б, где частота изменяется через равные промежутки времени от нижней рабочей частоты Fmin = F1 − ∆F

к верхней Fmin = F1 + ∆F и обратно.			Легко найти, что переходная фаза будет
меняться по пилообразному закону, так как
		T/ 2		∆ω 2π
	2ψmax = ∆ω ∫( 2C(t) −1)dt =			∆ω 2π	= mπ,
0				2Ω
или ψmax = mπ / 2, где m=∆ω/Ω – индекс частотной манипуляции.
		ω1	ωC	ωmax
			ωC
a	ωmin
a		T			t
		T			t
	-τ		0	τ

ψ(t) mπ/2

-mπ/2

Рис. 4.7. Закон изменения частоты и фазы при ЧМП

В выражении (4.13) cosψ и sinψ - периодические функции, так как изменение фазы ψ происходит периодически. Периодические функции f1 = cosψ и f2 = sinψ можно разложить в ряды Фурье

∞			∞
f (t) = a0 + ∑ak	cos kΩt +∑bk sin kΩt
k =1			k =1
и тем самым найти спектр сигнала.		a 0 ,	ak и b k	следует учесть, что в ин-
При вычислении коэффициентов		a 0 ,	ak и b k	следует учесть, что в ин-
тервале времени от 0 до Т/2	(или	π)	фаза ψ	изменяется по закону
				55

ψ = m(Ωt −π / 2), в интервале времени от Т/2 (или π) до Т (или 2π) – по закону ψ = m(3π / 2 − Ωt) . Тогда для функции f1 (t) = cosψ получим

2π

∫ f1

(t)dΩ1t

∫cos(Ωt

−π / 2)dΩ t +

2π

2π 0

2π

cos m(3π / 2 −Ωt)dΩ t =

sin m

;

∫

2π

πm

2π

∫ f1

(t)cos kΩtdΩ t =

sin m

2π

π(m2 − k 2 )

при чётном k; при нечётном k

получается ak =0.

2π

bk =

∫ f1(t)sin kΩtdΩ t =0 при всех k.

2π

Аналогично для функции f2 (t) = sinψ получим:

a0 = 0;

bk = 0;

∫sin m(Ωt −π / 2)coskΩtdΩ t +

2π

(4.14)

	1	2π	4m		π
+		∫ sin m(3π / 2 − Ωt)coskΩtdΩ t =		cosm
+	2π	∫ sin m(3π / 2 − Ωt)coskΩtdΩ t =	π(m2 − k 2 )	cosm	2
	2π	0	π(m2 − k 2 )		2

при нечётном k и ak = 0 при чётном k.

В результате напряжение после частотной манипуляции записывается в

виде

		2			∞		4m
U×ÌÏ (t) = U				sin mπ sinω1t + U ∑					sinm	π cos2kΩt +sinω1t +
			πm			π(m2	− (2k)2
∞				2	k =0			)		2
			4m		cos mπ cos(2k + 1)Ωtcosω1t.
+ U ∑
	π(m2	− (2k + 1)2 )
k =0					2

Заменив произведение косинусов и произведение синуса на косинус, окончательно получим

UЧМП

(t) =

(sin

sin ω1t +

2 cosm

cos(ω1 ± Ω)t +

−

± Ω

...).

− 22 sin m

2 sin(ω1

2 )t

2 − 32 cosm

2 cos(ω1

3 )t

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 7413 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>