5. Оцінка дисперсії випадкової величини :

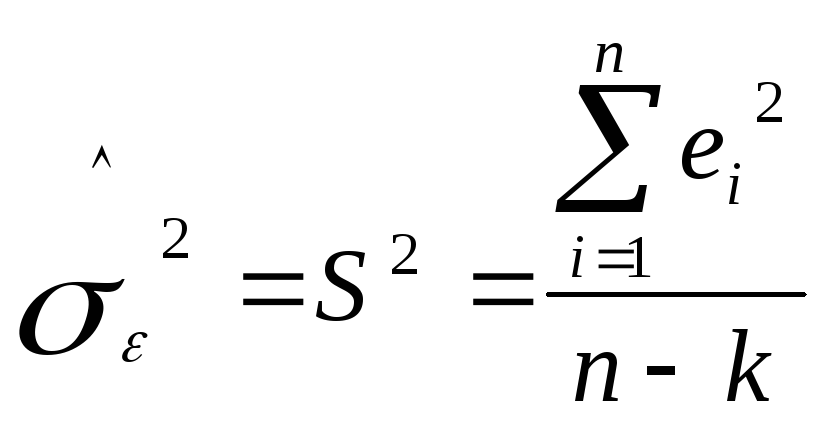, (2.6.5)

де к — кількість параметрів, що оцінюється в регресійній моделі. Для простої лінійної регресії:

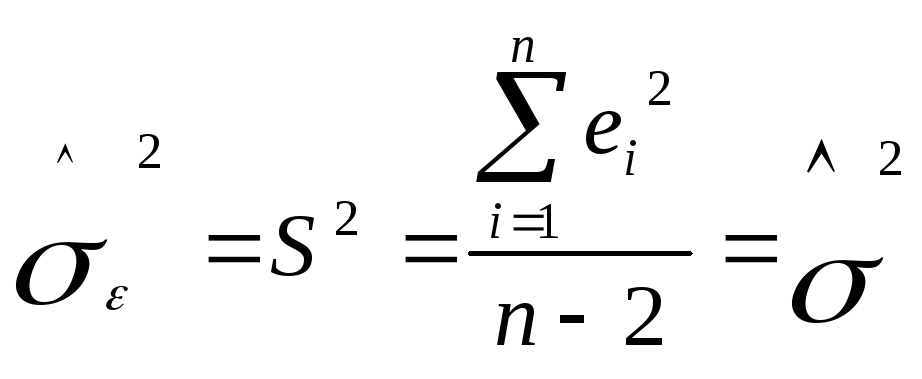. (2.6.6)

Середнє квадратичне відхилення оцінки дисперсії:

. (2.6.7)

Оскільки випадкова величина — неспостережувана, то і її дисперсію неможливо обчислити, тому на практиці дисперсія випадкової величинизамінюється на свою оцінку.

У виразах (2.6.2) та (2.6.4) дисперсія параметрів b₀ та b₁ — невідома, оскільки вона залежить від дисперсії помилок випадкової величини , котру неможливо спостерігати. Отже, для параметрівb₀ та b₁ дійсна дисперсія замінюється своєю оцінкою [5]:

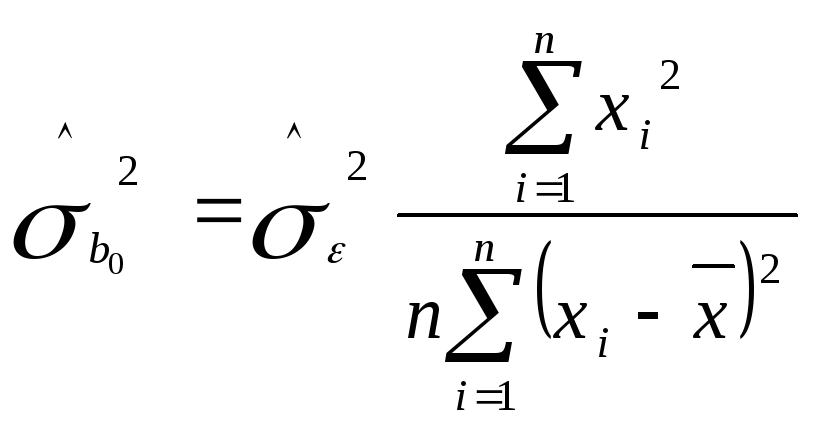; (2.6.8)

(2.6.9)

Приклад 5. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в прикладі 1.

Рішення:

Для параметра b_1:

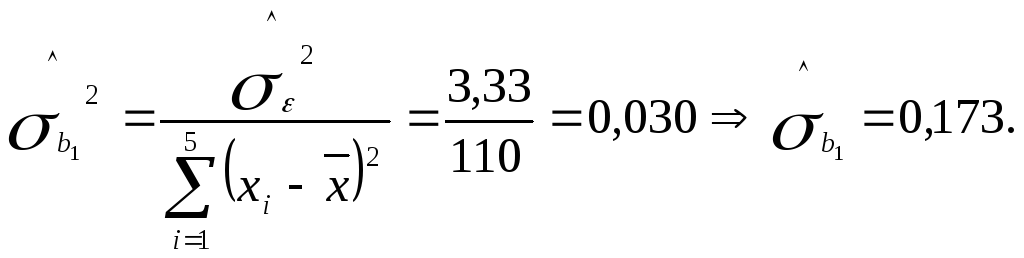
Для параметра b_0:

Завдання 21. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 4.

Завдання 22. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 8.

Завдання 23. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 10.

Завдання 24. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 11.

Завдання 25. Маємо таку інформацію:

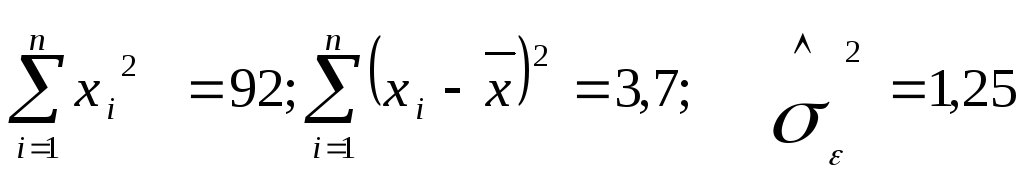; n = 40

а) визначити ; б) визначити .

7. Перевірка значимості параметрів b0 та b1 вибіркової лінійної регресійної моделі за допомогою t-теста Стьюдента

t-тест Стьюдента для перевірки значимості параметрів b₀ та b_1, визначених методом найменших квадратів, має вигляд:

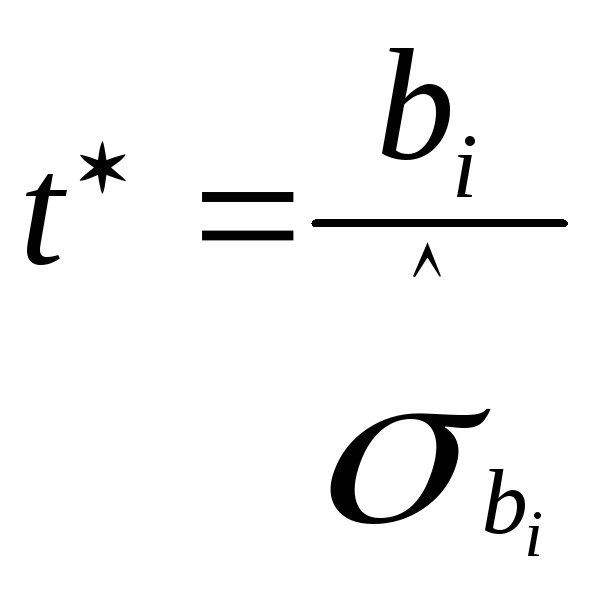. (2.7.1)

За таблицею t-розподілу Стьюдента визначають — критичне значення з (n-2) ступенями вільності та 5%-рівнем значимості.

Якщо , то параметр b_i — статистично значимий [5].

Приклад 6. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної

моделі, побудованої в прикладі 1, за допомогою

t-теста Стьюдента.

.

Рішення:

Для параметра b₁ та b₀:

_;

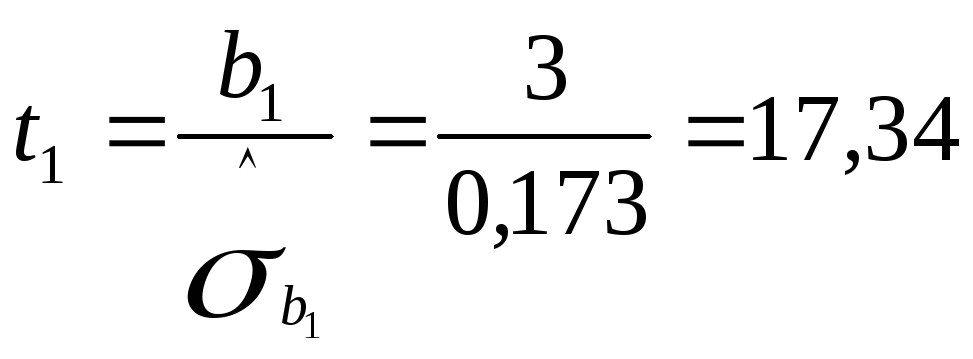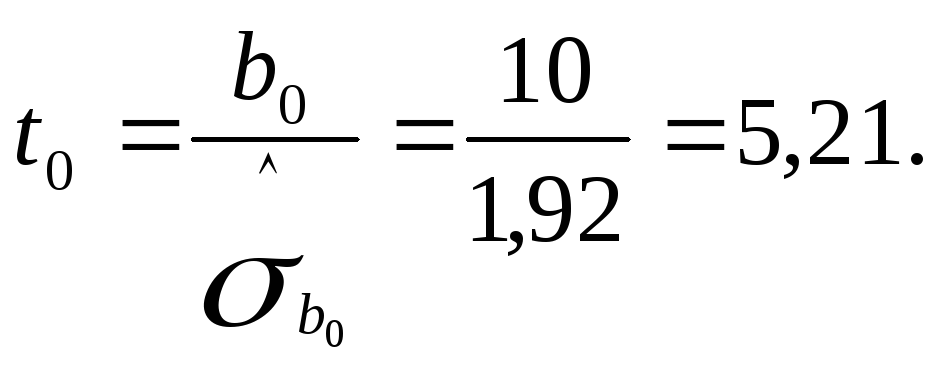
Примітка: та розраховані в прикладі 5. За таблицею t-розподілу Стьюдента визначимо — критичне значення з n-2=5-2=3 — ступенями вільності та 5%-рівнем значимості:

.

Оскільки, t₁=17,34 > t_кр.=3,182;

t₂ = 5,21 > t_кр.=3,182.

Отже, параметри b₁ та b₀ статистично значимі.

Завдання 26. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 4, використавши t-тест Стьюдента.

Завдання 27. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 8, використавши t-тест Стьюдента.

Завдання 28. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 10, використавши t-тест Стьюдента.

Завдання 29. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 11, використавши t-тест Стьюдента.

2.8. t-тест Стьюдента для оцінки значимості