2.5. Інші критерії якості лінійної регресії

Припустимо, відомі n прогнозних даних , що відповідаютьn

реальним даним у₁, у₂, у₃, …, у_n, тобто маємо відповідно n помилок прогнозу е₁, е₂, е₃, …, е_n . Для визначення якості прогнозу (моделі) на практиці широко використовуються такі критерії:

:

1. Середня помилка прогнозу:

(2.5.1)

Цей критерій характеризує ступінь зміщення прогнозу і для правильних прогнозів повинен прямувати до 0 за умови великої кількості спостережень, тобто

при .

2. Дисперсія помилок:

(2.5.2)

та стандартне відхилення:

(2.5.3)

Цей критерій вимірює ступінь розкиду значень змінної навколо свого середнього значення.

Для простої лінійної регресії середнє значення помилок дорівнює нулеві. Тому

. (2.5.4)

3. Абсолютне середнє відхилення:

. (2.5.5)

4. Середній квадрат помилки:

. (2.5.6)

Цей критерій для лінійної регресії збігається з дисперсією помилок

.

5. Абсолютна середня процентна помилка:

. (2.5.7)

Цей критерій використовується при порівнянні точності прогнозів різнорідних об’єктів, бо характеризує відносну точність прогнозу. При цьому вважається, якщо значення цього критерію менше 10% — висока точність прогнозу, а отже, і якість моделі; від 10 до 20% — добра точність; від 20 до 50% — задовільна точність; понад 50% — незадовільна точність

.

6. Середня процентна помилка:

. (2.5.8)

Це показник незміщеності прогнозу. З точки зору практики для якісних моделей цей показник має бути малим, загалом не перевищувати 5%. Зазначимо, що як і показник 5, він не визначений для нульових значень у [5]

.

7. Середня абсолютна помилка:

Примітка: Для розрахунку вищеперелічених критеріїв варто використати таблицю:

№
1 2 3 . . . n

Завдання 17. Перевірити якість лінійної регресійної моделі, побудованої в завданні 4, за допомогою критеріїв:

Зробити висновки.

Завдання 18. Перевірити якість лінійної регресійної моделі, побудованої в завданні 8, за допомогою критеріїв:

Зробити висновки.

Завдання 19. Перевірити якість лінійної регресійної моделі, побудованої в завданні 10, за допомогою критеріїв з розділу 2.5. Зробити висновки.

Завдання 20. Перевірити якість лінійної регресійної моделі, побудованої в завданні 11, за допомогою критеріїв з розділу 2.5. Зробити висновки.

2.6. Математичне сподівання та дисперсія розподілу параметрів b0 та b1 . Оцінка дисперсії випадкової величини .

1. Математичне сподівання параметра b₀ дорівнює:

. (2.6.1)

2. Дисперсія параметра b0:

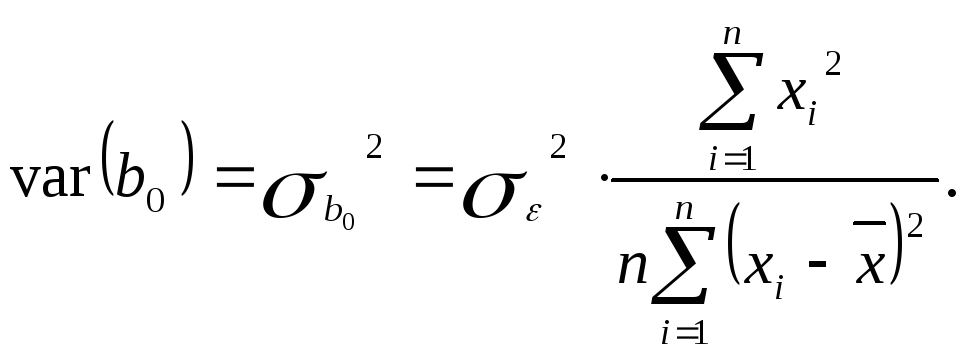(2.6.2)

3. Математичне сподівання параметра b₁ дорівнює:

. (2.6.3)

4. Дисперсія параметра b1:

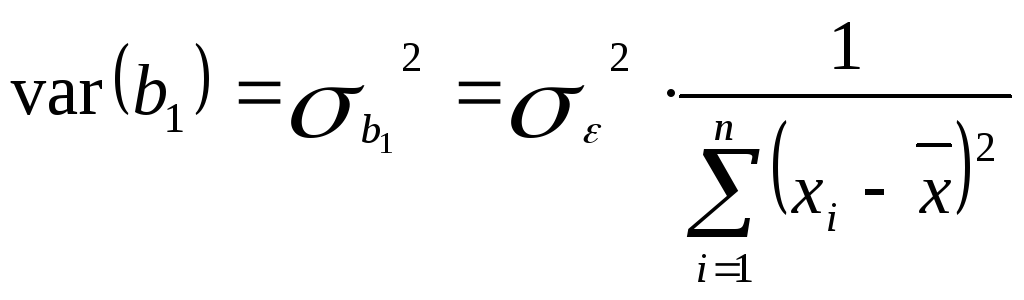, (2.6.4)

де — дисперсія залежної змінної.