2. Проста вибіркова лінійна регресія

Прості лінійні регресійні моделі встановлюють лінійну залежність між двома змінними, наприклад, витратами на відпустку та складом родини; витратами на рекламу та обсягом продукції, що випускається; витратами на споживання та валовим національним продуктом (ВНП), зміною ВНП залежно від часу, врожайністю культур та кількістю добрив, що вносяться під культури.

При цьому одна зі змінних вважається залежною змінною (y) та розглядається як функція від незалежної змінної (x).

У загальному вигляді проста вибіркова лінійна регресійна модель запишеться так:

(2.0)

де y — вектор спостережень за залежною змінною;

;

х — вектор спостережень за незалежною змінною;

;

b₀,b₁ — невідомі параметри регресійної моделі;

е — вектор випадкових величин (помилок);

. [5]

2.1. Оцінка параметрів лінійної регресії за допомогою методу найменших квадратів

Щоб мати явний вид залежності, необхідно знайти (оцінити) невідомі параметри b₀, b₁ цієї моделі за допомогою критерію. Найпоширенішим є критерій мінімізації суми квадратів відхилень. Логічно, що треба проводити пряму таким чином, щоб сума квадратів помилок була мінімальною. В цьому і полягає критерій найменших квадратів: невідомі параметри b₀ та b₁ визначаються таким чином, щоб мінімізувати , тобто

(2.1.1)

Визначимо значення b₀ та b₁, котрі мінімізують вираз (2.1.1). Рішення системи двох лінійних нормальних рівнянь:

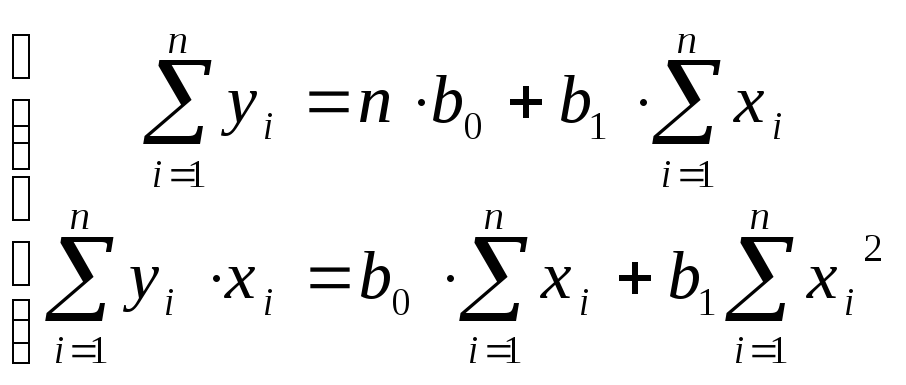(2.1.2)

дозволяє одержати такі значення параметрів b₁ та b₀:

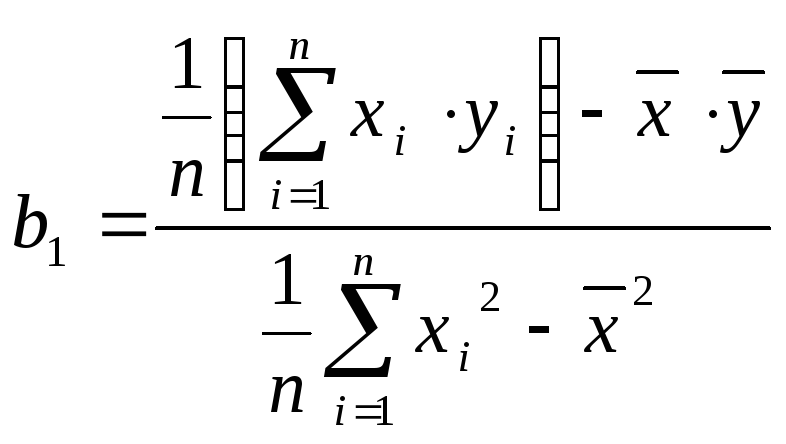, (2.1.3)

де ; ;

. (2.1.4)

В явному вигляді регресія у від х, у якій параметри обчислені за методом найменших квадратів, виразиться так:

або . (2.1.5) [5]

Приклад 1. Побудувати лінійну регресійну модель, що характеризує залежність між обсягом продажу цукерок фабрики “Світоч” (млн. коробок) та витратами на рекламу (млн. грн.), на основі вихідних даних:

п/п	Обсяг продажу, млн. коробок	Витрати на рекламу, млн. грн.
1 2 3 4 5	25 30 35 45 65	5 6 9 12 18

Рішення:

В таблиці представимо результати попередніх розрахунків:

№ п/п	Обсяг продажу, млн.коробок, yi	Витрати на рекламу, млн. грн., xi			^	^
1 2 3 4 5	25 30 35 45 65	5 6 9 12 18	125 180 315 540 1170	25 36 81 144 324	25 28 37 46 64	0 2 -2 -1 1
	200 40	50 10	2330 466	610 122	200 40	0 0

Розрахуємо параметри b₁ та b₀:

;

.

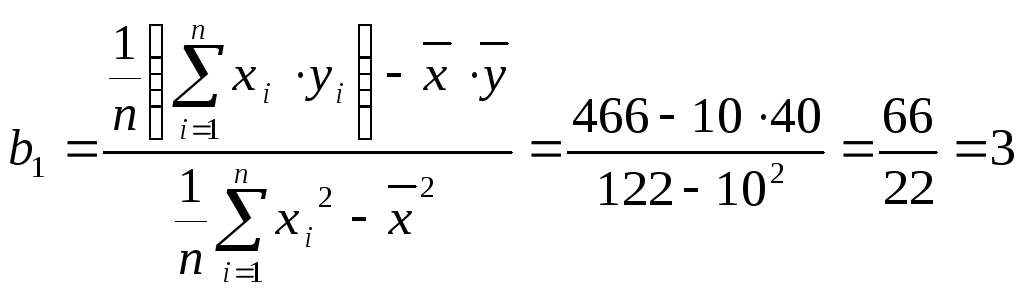Таким чином, лінійна регресійна модель має вигляд:

або .

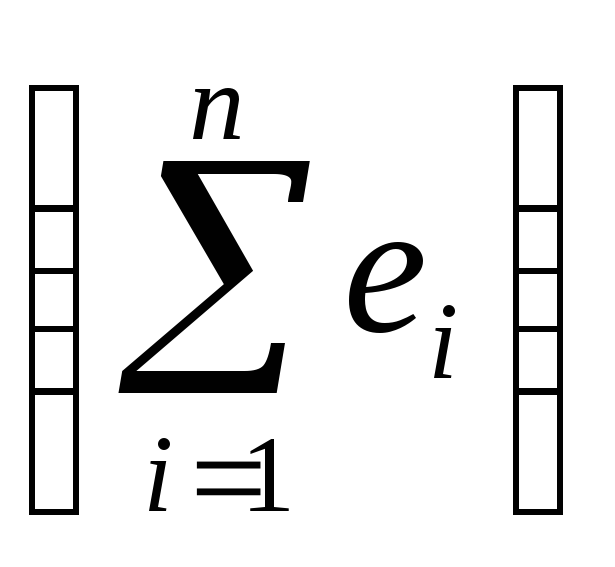Зазначимо, що сума оцінених (розрахункових) значень обсягу продажу цукерок () дорівнює сумі фактичних значень y_i, а сума помилок дорівнює нулю.

Завдання 1. Припустимо, що ви зібрали дані про споживання домашніх господарств в Україні та їх доходів і оцінили таке рівняння: С = 120 + 0,75у

Визначити: а) яка змінна є залежною, а яка — незалежною;

б) пояснити взаємозв’язок між споживанням та доходом. На скільки зросте споживання, якщо доход зросте на 1 одиницю?

Завдання 2. Припустимо, ви зібрали дані про річний продаж фірмою “Україна” продукції (у) і суми, які використано на наукові дослідження (х). Ви маєте таку статистику:

коваріація:

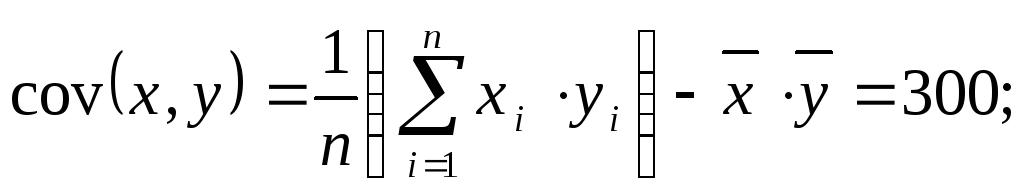
варіація:

варіація: .

Середній річний продаж: ()=1200.

Середня сума на наукові дослідження: ()=895.

Визначити параметри регресії b₀ та b₁ і побудувати лінійну регресійну модель. Дати економічну інтерпретацію одрежаній моделі.

Завдання 3. Є такі дані:

х	У
20 14 12 20 33 38	75 85 92 88 72 99

Заповнити пропуски і знайти параметри регресії b₀ та b₁.

Завдання 4. Маємо дані про урожайність зернових (y_i) і кількість внесених на 1 га мінеральних добрив (x_i) під зернові за 10 років в ПОК “Зоря” Білозерського району Херсонської області:

Роки	1999	2000	2001	2002	2003	2004	2005	2006	2007	2008
Урожайність, ц/га, yi	65,2	64,4	54,0	54,7	64,0	31,6	44,7	32,3	54,5	46,8
Внесено мін.добрив, ц.д.р. на 1 га, xi	2,6	2,5	2,1	2,2	2,3	1,6	1,8	2,1	2,0	1,9

Побудувати лінійну регресійну модель, що характеризує залежність між урожайністю зернових та кількістю внесених на 1 га мінеральних добрив.