Коефіцієнта кореляції

t-тест для оцінки значимості коефіцієнта кореляції (з припущенням, що ):

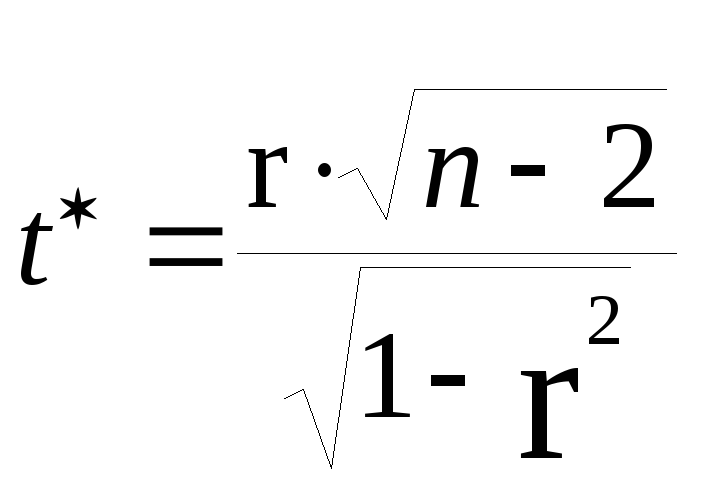, (2.8.1)

де r — вибірковий коефіцієнт кореляції між х і у;

n — кількість спостережень.

Величина t* розподілена за t-розподілом Стьюдента з (n-k)- ступенями вільності (для простої лінійної регресії к=2).

Розраховане значення t* порівнюємо з критичним при-ному рівні значимості й (n-2)-ступенях вільності. Якщо , відкидаємо нуль-гіпотезу і приймаємо гіпотезу, тобто робимо висновок, що коефіцієнт кореляції — статистично значимий [5].

Приклад 7. Маємо вибірку значень х і у, яка складається з 5 спостережень,коефіцієнт кореляції r _yx = 0,995. Перевірити при 5%-ному рівні значимості, чи значимо коефіцієнт кореляції відрізняється від нуля.

Рішення: t-статистика Стьюдента:

.

За таблицями Стьюдента знаходимо критичне значення (t_кр.) з 3-ма ступенями вільності і 5%-ним рівнем значимості, яке дорівнює .Оскільки,t* =17,23 > t_кр. = 3,182, то робимо висновок, що , тобто коефіцієнт кореляції значимо відрізняється від нуля.

Завдання 30. Перевірити при 5%-ному рівні значимості , чи значимо відрізняється від нуля коефіцієнт кореляції, розрахований в завданні 6.

Завдання 31. Перевірити при 5%-ному рівні значимості , чи значимо відрізняється від нуля коефіцієнт кореляції, розрахований в завданні 7.

Завдання 32. Здійснити перевірку значимості коефіцієнта кореляції (при 5%-ному рівні значимості), розрахованого в завданні 8.

Завдання 33. Здійснити перевірку значимості коефіцієнта кореляції (при 5%-ному рівні значимості), розрахованого в завданні 10.

Завдання 34. Перевірити при 5%-ному рівні значимості, чи значимо відрізняється від нуля коефіцієнт кореляції, визначений в завданні 11

.

2.9. Побудова інтервалів довіри для параметрів та 

Для того, щоб визначити, як же параметри b₀ та b₁ вибіркової лінійної регресії пов’язані параметрами _та _узагальненої лінійної регресії, потрібно побудувати інтервали довіри для параметрів [5]:

з (n-2) ступенями вільності

або

. (2.9.1)

Для 95%-ного рівня довіри:

. (2.9.2)

Приклад 8. Побудувати інтервали довіри для параметрів _та _лінійної регресійної моделі, розрахованої в прикладі 1 (рівень довіри — 95%).

Рішення: Інтервали довіри для параметра _:

або

Інтервали довіри для параметра _

_або

Висновок: інтервали довіри для параметра _сталіші, ніж для параметра _.

Завдання 35. Побудувати інтервали довіри для параметрів _та _лінійної регресійної моделі, розрахованої в завданні 4 (рівень довіри — 95%).

Завдання 36. Побудувати інтервали довіри для параметрів _та _лінійної регресійної моделі, розрахованої в завданні 8 (рівень довіри — 95%).

Завдання 37. Побудувати інтервали довіри для параметрів _та _лінійної регресійної моделі, розрахованої в завданні 10 (рівень довіри — 95%).

Завдання 38. Побудувати інтервали довіри для параметрів _та _лінійної регресійної моделі, розрахованої в завданні 11 (рівень довіри — 95%).

Завдання 39. Оцінюємо таку регресію:

У=2300 + 10,12х;

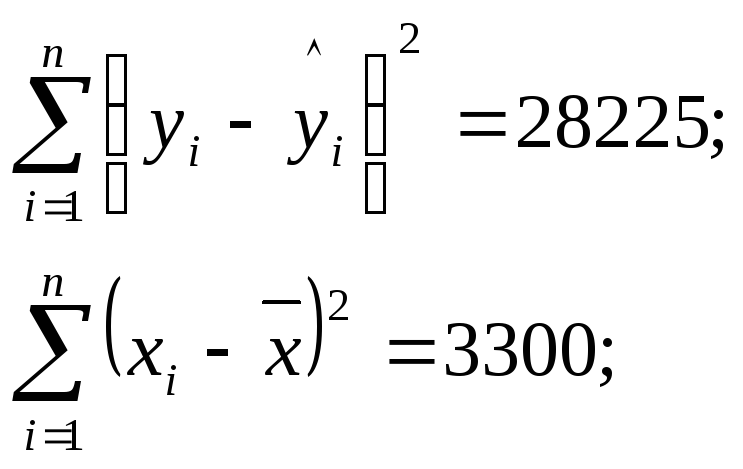
n=28.

Перевірити значимість нахилу при 95%-ному рівні довіри. Побудувати 90%-ний інтервал довіри для нахилу.