
- •Многочлени. Дії над ними.
- •Означення многочлена від однієї змінної
- •Дії над многочленами
- •Теорема про ділення многочленів з остачею
- •Подільність многочленів. Дільники. Спільні дільники. Алгоритм Евкліда знаходження нсд двох многочленів.
- •Означення спільного дільника та найбільшого
- •Алгоритм Евкліда знаходження нсд двох многочленів .
- •Корені многочленів.Теорема Безу. Схема Горнера
- •Основна теорема алгебри комплексних чисел та наслідки з неї.
- •(Без доведення).
- •Алгебраїчне знаходження коренів многочлена.
- •Многочлени над полем раціональних чисел.
- •Властивості незвідних у полі многочленів
- •Знаходження раціональних коренів многочленів з раціональними (цілими) коефіцієнтами.
- •Раціональні дроби
- •Межі дійсних коренів многочленів з дійсними коефіцієнтами.
- •Теорема Штурма. Кількість дійсних коренів многочлена - ними коефіцієнтами.
- •3 0 0 -5 3
- •Відокремлення коренів методом Штурма.
Раціональні дроби
Хоча основним завданням даного розділу є вивчення многочленів (цілих раціональних функцій), у даному параграфі розглянемо питання, що стосується дробово – раціональних функцій. Це питання має важливе значення для математичного аналізу (зокрема, для інтегрального числення), але за своїм математичним змістом воно алгебраїчне і безпосередньо пов’язане з розкладанням многочленів на незвідні множники .
Означення
1. Раціональним
дробом (або дробово – раціональною
функцією) над полем
![]() називається функція вигляду
називається функція вигляду
![]() ,
,
де
![]() - деякі многочлени над полем
- деякі многочлени над полем![]() ;
;![]() .
.
Означення
2. Два
раціональні дроби
![]() та
та![]() називаються рівними:
називаються рівними:
![]() =
=![]() ,
якщо
,
якщо![]() .
.
Звідси маємо, що кожен раціональний дріб можна домножити (скоротити) на довільний ненульовий спільний множник:
![]() =
=![]() ,
,![]() .
.
Означення
3. Раціональний
дріб
![]() називається правильним, якщо степінь
називається правильним, якщо степінь![]() <
степеня
<
степеня![]() і
відповідно, неправильним, якщо степінь
і
відповідно, неправильним, якщо степінь![]()
![]() степеня
степеня![]() .
.
Означення
4. Раціональний
дріб
![]() називається нескоротнім, якщо НСД
називається нескоротнім, якщо НСД![]() .
У протилежному випадку дріб називається
скоротним.
.
У протилежному випадку дріб називається
скоротним.
Наприклад
а)
![]() -
неправильні дроби
-
неправильні дроби
![]() -
нескоротній дріб;
-
нескоротній дріб;
![]() -скоротній
дріб.
-скоротній
дріб.
б)
![]() -правильний
нескоротній дріб.
-правильний
нескоротній дріб.
в)
![]() -неправильний
нескоротній дріб.
-неправильний
нескоротній дріб.
Теорема
1. Кожен
раціональний дріб
![]() дорівнює деякому нескоротному дробу,
який визначається єдиним чином з точністю
до спільного для чисельника та знаменника
ненульового множника нульового степеня:
дорівнює деякому нескоротному дробу,
який визначається єдиним чином з точністю
до спільного для чисельника та знаменника
ненульового множника нульового степеня:
![]() =
=![]() ,
,
де НСД![]() ,
,![]() .
.
Доведення:
Нехай
![]() - даний раціональний дріб, у якого НСД
- даний раціональний дріб, у якого НСД![]() .Тоді
чисельник та знаменник цього дробу
можна скоротити на
.Тоді
чисельник та знаменник цього дробу
можна скоротити на
![]() ,
після чого отримаємо рівний йому
нескоротний дріб. Далі, якщо два нескоротні
дроби рівні
,
після чого отримаємо рівний йому
нескоротний дріб. Далі, якщо два нескоротні
дроби рівні![]() ,(*)
то
із того, що
,(*)
то
із того, що
![]() та
та![]() маємо, що:
маємо, що:
а)
![]() ;
;
б)
![]() .
Аналогічно, враховуючи (*), маємо:
.
Аналогічно, враховуючи (*), маємо:![]() .
.
Отже, теорему доведено.
Над раціональними дробами можна виконувати арифметичні дії за тими ж законами, що і над звичайними числовими дробами.
Додавання (віднімання):
![]() при
при
![]()
Множення :
![]() при
при
![]()
Ділення:
![]() при
при
![]()
Виконується при цьому властивості асоціативності та комунікативності дій додавання та віднімання; існують обернені елементи при дії додавання (протилежний дріб) та при дії множення (обернений дріб до ненульового дробу).
Отже, множина всіх раціональних дробів відносно дій додавання та множення дробів утворює поле, яке називають полем раціональних дробів.
Теорема 2: Довільний раціональний дріб можна подати у вигляді суми многочлена та правильного раціонального дробу. Причому таке зображення єдине.
Доведення:
Нехай
![]() - єдиний раціональний дріб
- єдиний раціональний дріб![]() .
Поділивши
.
Поділивши![]() на
на![]() ,
матимемо:
,
матимемо:![]() де степінь
де степінь![]() <
степеня
<
степеня
![]() .Тоді
.Тоді
![]() =
=![]() (1),
де
(1),
де
![]() многочлен,
многочлен,
![]() - правильний раціональний дріб.
- правильний раціональний дріб.
Покажемо,
що таке зображення (1) єдине. Припустимо,
що має місце ще одна рівність: (1´)
![]() ,
де степінь
,
де степінь![]() <
степеня
<
степеня
![]() ,
,
![]() -
многочлен.
-
многочлен.
Із (1) та (1´), прирівнюючи ліві частини, маємо:
![]()
![]()
![]()
Зліва в останній рівності многочлен, а справа – раціональний дріб, який є правильним (різниця правильних дробів). Тому вони рівні тоді і тільки тоді, коли є нульовими:
 зображення
(1) – єдине.
зображення
(1) – єдине.
Отже, теорему доведено.
Нагадуємо
(§ 4.8), що незвідними у полі
![]() є многочлени першого степеня вигляду
є многочлени першого степеня вигляду![]() ,
та многочлени другого степеня вигляду
,
та многочлени другого степеня вигляду![]() .
.
Означення
6. Правильний
раціональний дріб
![]() називається простим, елементарним якщо:а)
степінь
називається простим, елементарним якщо:а)
степінь
![]() <
степеня
<
степеня
![]() ;
;
б)
![]() - незвідний многочлен.
- незвідний многочлен.
Приклади.
1.
![]() - не простий
- не простий![]() ;
;
2.
![]() - простий;
- простий;
3.
![]() - не простий
- не простий![]() ;
;
4.
![]() - простий.
- простий.
Теорема 3 (основна теорема про раціональні дроби).
Довільний правильний раціональний дріб розкладається в суму простих дробів.
Доведення.
Нехай
![]() - заданий правильний раціональний дріб
(
- заданий правильний раціональний дріб
(![]() ,степінь
,степінь![]() <
степеня
<
степеня
![]() ).
).
Доведення теореми складається з кількох кроків.
І). Нехай знаменник раціонального дробу розкладається на добуток взаємно простих многочленів:
![]()
Тобто
![]() (2)
(2)
Покажемо,
що тоді дріб
![]() можна розкласти на суму дробів,
знаменниками яких є многочлени
можна розкласти на суму дробів,
знаменниками яких є многочлени
![]() та
та
![]() .
.
Оскільки
![]() ,
то
,
то![]() такі многочлени, що
такі многочлени, що
![]() (3)
(3)
Поділимо
тепер
![]() на
на
![]() :
:
![]()
де
степінь
![]() <
степеня
<
степеня
![]() .
Підставимо останню рівність у (3):
.
Підставимо останню рівність у (3):
![]() (3´)
(3´)
У
останній рівності маємо, що степінь
![]() <
степеня
<
степеня
![]() ,
,
![]() степінь
степінь![]() <
степеня
<
степеня
![]() .
.
Крім
того, степінь
![]() <
степеня
<
степеня
![]() (4)
(4)
бо із (3´) :
![]() та
степінь
та
степінь
![]() <
степеня
<
степеня
![]() ,
,
степінь
![]() <
степеня
<
степеня
![]() .
.
А тому,
із (4) маємо, що степінь
![]() <
степеня
<
степеня
![]() .
Підставимо
(3´) у (2):
.
Підставимо
(3´) у (2):
![]()
![]()
![]() ,
,
причому
степінь
![]() <
степеня
<
степеня
![]() ;
степінь
;
степінь
![]() <
степеня
<
степеня
![]() .
.
Отже,
дроби
![]() та
та![]() - правильні.
- правильні.
Висновок:
якщо
знаменник
![]() правильного раціонального дробу
розкладається на добуток взаємно простих
многочленів
правильного раціонального дробу
розкладається на добуток взаємно простих
многочленів
![]() ,
то такий дріб розкладається на суму
правильних дробів, знаменниками яких
є многочлени
,
то такий дріб розкладається на суму
правильних дробів, знаменниками яких
є многочлени
![]() та
та
![]() .
.
Якщо отриманих правильних дробів знову розкладаються на добуток взаємно простих многочленів, то кожен з цих дробів розкладається на суму правильних дробів і т. д..
Цей
процес продовжується до тих пір, поки
не прийдемо до дробів, знаменники яких
є незвідними многочленами
![]() полі
полі![]() (тобто вже не розкладається на взаємно
прості множники) або степені цих незвідних
многочленів. Тобто знаменники дробів
матимуть вигляд
(тобто вже не розкладається на взаємно
прості множники) або степені цих незвідних
многочленів. Тобто знаменники дробів
матимуть вигляд![]() ,
де
,
де![]() - незвідний у полі
- незвідний у полі![]() многочлен.
многочлен.
ІІ).
Нехай
тепер у правильному раціональному дробі
![]() знаменник
знаменник![]() розкладається на добуток незвідних
розкладається на добуток незвідних![]() полі
полі![]() многочленів (Згідно з п.4.8.1, такий розклад
єдиний з точністю до порядку запису
співмножників):
многочленів (Згідно з п.4.8.1, такий розклад
єдиний з точністю до порядку запису
співмножників):
![]() ,
,
де
![]() - незвідні многочлени над полем
- незвідні многочлени над полем![]() .
.
Тоді, враховуючи першу частину доведення цієї теореми маємо:
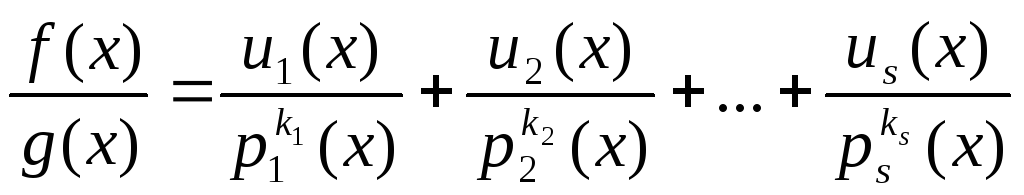 ,
(5)
,
(5)
де
степінь
![]() <
степеня
<
степеня
![]() ,
тобто
всі доданки у (5) є правильними, але не
простими дробами.
,
тобто
всі доданки у (5) є правильними, але не
простими дробами.
ІІІ).
Розглянемо
тепер правильний дріб
![]() ,
де
,
де![]() - незвідний у полі
- незвідний у полі![]() многочлен.
многочлен.
З´ясуємо,
як саме цей правильний дріб розкласти
на суму простих дробів. Очевидно, що
степінь
![]() <
степеня
<
степеня
![]() .
.
Поділимо
![]() на
на![]() :
:
![]() ,
але степінь
,
але степінь
![]() степеня
степеня![]() (6)
(6)
Ділимо
потім
![]() на
на![]() :
:
![]() але
степінь
але
степінь
![]() степеня
степеня![]() ,
та степінь
,
та степінь![]() степеня
степеня![]() і
т. д.
(7)
і
т. д.
(7)
Нарешті можна отримати:
![]() степінь
степінь
![]() степеня
степеня![]() ,
та степінь
,
та степінь![]() степеня
степеня![]() .
(8)
.
(8)
Підставляючи ці рівності одна в одну знизу вверх, отримаємо:
![]() .
.
Поділимо
тепер обидві частини цієї рівності на
![]() .
Маємо:
.
Маємо:
![]() ,
,
де
степінь
![]() <
степеня
<
степеня
![]()
степінь
![]() <
степеня
<
степеня
![]() ,
тобто кожен з доданків – простий дріб.
,
тобто кожен з доданків – простий дріб.
Висновок:
кожен
правильний дріб вигляду
![]() ,
де
,
де![]() - незвідний у полі
- незвідний у полі![]() многочлен,
многочлен,![]() ,
можна подати у вигляді простих дробів:
,
можна подати у вигляді простих дробів:
![]() ,
(степінь
,
(степінь
![]() <
степеня
<
степеня
![]() ).
).
Виконуючи аналогічні розклади для кожного з дробів у (5), отримуємо твердження теореми.
Теорему доведено.
Нагадуємо
(див. § 4.8, теореми 2 і 3), що в полі дійсних
чисел
![]() незвідними є многочлени 1 – го степеня
вигляду
незвідними є многочлени 1 – го степеня
вигляду![]() та многочлени 2 – го степеня вигляду
та многочлени 2 – го степеня вигляду![]() .
.
Тому, враховуючи основну теорему про раціональні дроби (алгоритм її доведення), можемо сформулювати наступний наслідок:
Наслідок:
Нехай
![]() - правильний дріб (
- правильний дріб (![]() многочлени з дійсними коефіцієнтами).
Нехай
многочлени з дійсними коефіцієнтами).
Нехай![]() - розкладаємо на незвідні множники 1 –
го і 2 –го степеня. Тоді,
- розкладаємо на незвідні множники 1 –
го і 2 –го степеня. Тоді,
![]()
розклад даного добутку на прості дроби. (10)
(![]() ).
).
Зауваження
1. У
полі комплексних чисел
![]() дріб
дріб![]() розкладається
розкладається
лише на
прості дроби вигляду
![]()
Зауваження
2. У
випадку розкладу дробу
![]() у полі дійсних чисел
у полі дійсних чисел![]() (або комплексних чисел
(або комплексних чисел![]() )
чисел зручно користуватися методом
невизначених коефіцієнтів.
)
чисел зручно користуватися методом
невизначених коефіцієнтів.
Цей метод полягає у наступному.
Дріб
![]() записуємо у вигляді (10) з невизначеними
(буквенними) коефіцієнтами. Помножуємо
потім обидві частини отриманої рівності
на
записуємо у вигляді (10) з невизначеними
(буквенними) коефіцієнтами. Помножуємо
потім обидві частини отриманої рівності
на![]() .
Отримуємо рівність двох многочленів,
порівнюємо коефіцієнти біля відповідних
степенів змінної
.
Отримуємо рівність двох многочленів,
порівнюємо коефіцієнти біля відповідних
степенів змінної![]() .
.
Приклади:
1). Розкласти на суму простих дробів раціональний дріб.
![]()
![]()

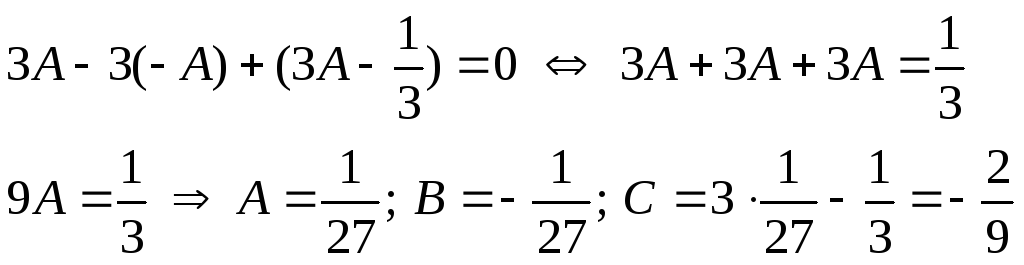
Отже,
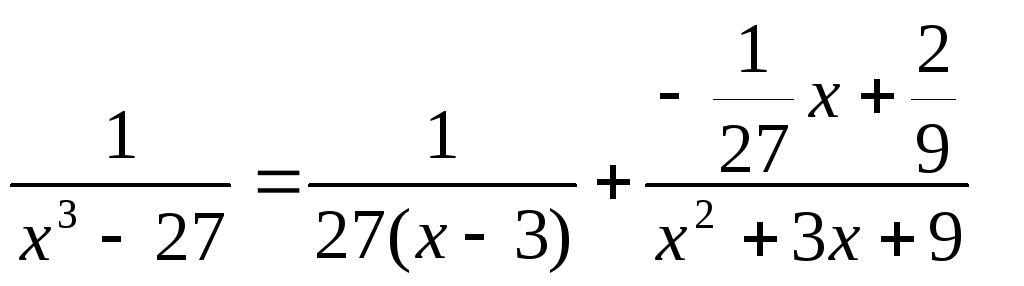 .
.
2).
![]()
![]()
Коефіцієнт
![]() шукаємо як у попередньому прикладі.
шукаємо як у попередньому прикладі.
