Многочлени над полем раціональних чисел.

Звідність і незвідність многочленів.

Як вже нагадували вище, для многочленів можна вказати розклади на множники, аналогічні розкладу цілих чисел на добуток простих множників. Визначимо спочатку ті многочлени, які відіграють в кільці многочленів аналогічну роль, яку в кільці відіграють прості числа.

Зауважимо, що будемо далі вивчати многочлени, степінь яких .

Знаємо, що будь-який многочлен ділиться на будь-яке ненульове число. Тобто можна записати, що , де

Нехай задано многочлен ,, з коефіцієнтами з поля .

Означ.1. Многочлен ,, з коефіцієнтами з поля називається звідним у полі, якщо його можна подати у вигляді добутку двох многочленів:

з коефіцієнтами з поля , степені яких менше ніж:

У протилежному випадку, називається незвідним у полі.

Отже, – звідний

–незвідний

Зауважимо, що про звідністьможна говорити лише відносно деякого поля, оскільки многочлен, незвідний у деякому полі, може бути звідним у розширенні цього поля.

Наприклад.

1) – незвідний у полі.

–звідний у полі .

2) – незвідний у полі.

–звідний у полі .

3) – звідний у полі.

Властивості незвідних у полі многочленів

1. Кожен многочлен першого степеня є незвідним у полі .

2. Якщо деякий многочлен 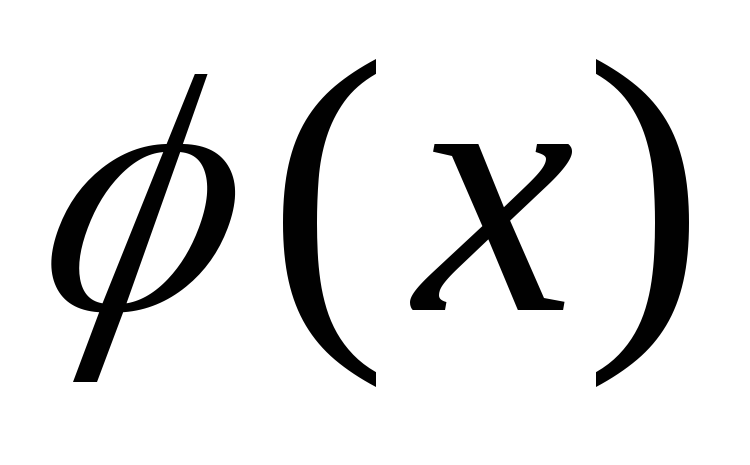– незвідний у полі, то незвідним буде і многочлен

3. Якщо добуток , де– незвідний многочлен, то хочаб один з многочленівабоділиться на.

4. Якщо 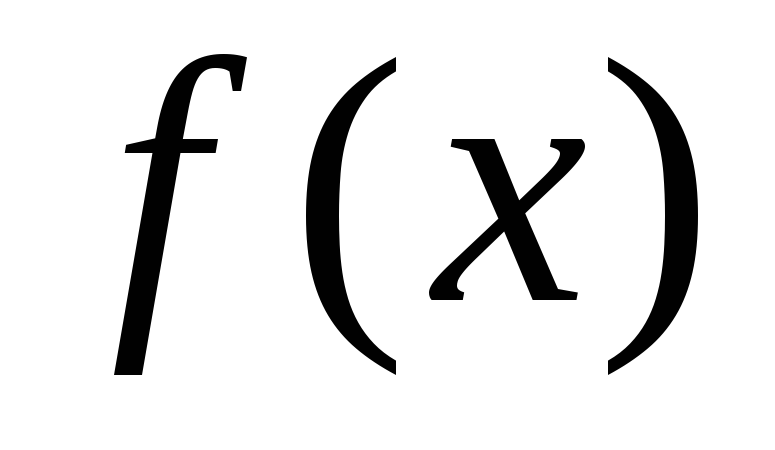– довільний многочлен,– незвідний многочлен, то або, абоівзаємно прості.

Теорема 1. Довільний многочлен з коефіцієнтами з полястепенярозкладається на добуток незвідних множників.

Такий розклад єдиний з точністю до запису співмножників.

(без доведення).

Теорема 2. У полі незвідними є лише многочлени першого степеня вигляду

Теорема 3. У полі незвідними є лише многочлени першого степеня з дійсними коефіцієнтами вигляду , які відповідають дійсним кореням та многочлени другого степеня з дійсними коефіцієнтами вигляду , які відповідають парам комплексних спряжених коренів (дискримінант квадратного тричлена менше нуля: ).

Теорема 4. Многочлен з раціональними коефіцієнтами степенябуде звідним у полі, якщо він має хоч один раціональний корінь.

Теорема 5. Якщо многочлен з цілими коефіцієнтами незвідний у множині цілих чисел, то він буде незвідним у множині.

(без доведення).

За допомогою наступної теореми можна розв’язувати питання про незвідність многочленів з цілими коефіцієнтами у полі .

Критерій Ейзенштейна (достатня умова незвідності многочлена у полі ):

Якщо у многочлені з цілими коефіцієнтами

і якщо існує таке просте число , що:

1) коефіцієнти

2)

3)

то многочлен – незвідний у полі.

(без доведення).

Наприклад:

1)

–незвідний у полі .

(цей многочлен має корені , але).

2) – звідний у полі, бо немає простого, щоб виконати умови критерію Ейзенштейна.

3) – незвідний у полі, бо

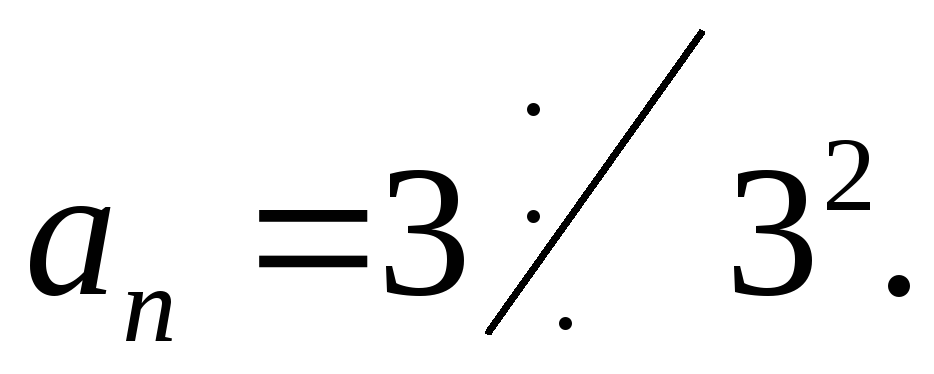
Зауваження: Із критерію Ейзенштейна існування многочленів довільного ненульового степеня з цілими коефіцієнтами, незвідні у полі.