Теорема про ділення многочленів з остачею

Існує метод для практичного розв’язання питання, коли результат ділення двох многочленів є многочленом. Це – алгоритм ділення з остачею, відомий нам з елементарної математики для чисел.

Теорема (про ділення многочленів з остачею): Для двох довільних многочленів таіснує єдина пара многочленівта, що

(5)

де (6)

Доведення. Єдність (від супротивного).

Нехай існують ще два многочлени та, які задовольняють аналогічну умову до (5):

()

де ()

Прирівнюючи праві частини рівностей (5) і () і зводячи подібні, маємо:

(7)

але, оскільки , то,

тому

а тоді у рівності (7) зліва многочлен має степінь , тобто має степінь більший, ніж степінь многочлена справа, що неможливо. Отже,

Многочлени ізнаходяться з умов (5) і (6) однозначно.

Існування. Нехай

1. Якщо, , (),

то можна покласти

умови (5) і (6) виконуються.

2. Якщо, 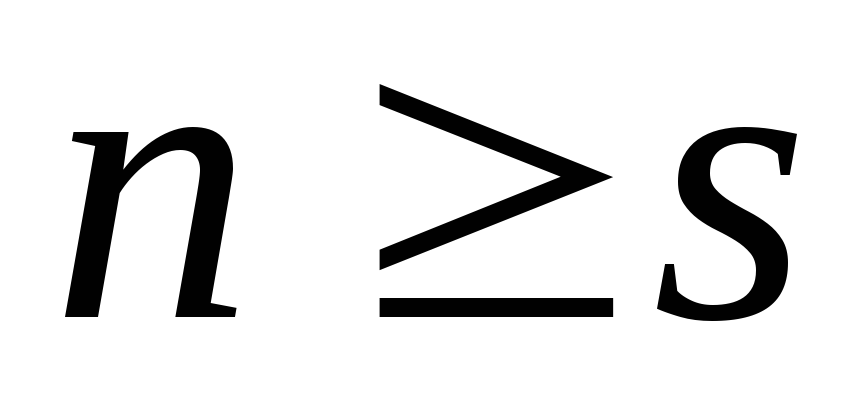, то скористаємося методом ділення многочленів, розташованих за спадними степенями змінноїx:

Розглянемо многочлен

(8)

Позначимо: , старший коефіцієнт многочленна.

Тоді формулу (8) можна переписати так:

Може статися, що або

а тому можемо вибрати ;– потрібні нам многочленита.

Якщо ж (), то покладемо

()

то позначимо

старший коефіцієнт

Нескладно переконатися, що , тобто

Далі, якщо і, то покладемо умову

()

і т.д.

Оскільки степені побудованих многочленів спадають:

то після скінченої кількості кроків отримаємо такий многочлен , що

()

та .

Тоді зупиняємо процес побудови додаткових многочленів .

Додамо тепер рівності (8), (), (), … , (). Отримаємо:

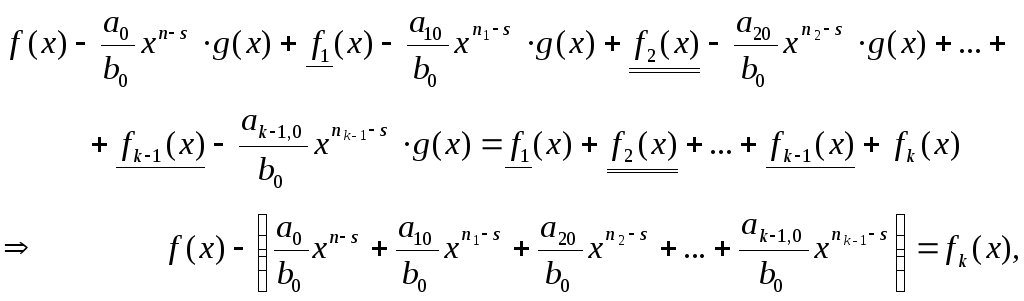
Позначимо тепер

, де .

Многочлени тазадовольняють потрібні вимоги теореми, що і доводить їх існування.

Теорему доведено повністю.

Зауваження 1: Коефіцієнти многочленів , а тому і коефіцієнти многочленівтавиражаються через коефіцієнти многочленівта. А тому вони будуть із того ж поляP, що й коефіцієнти та.

Зауваження 2: Многочлен називається неповною часткою, а многочлен– остачею.

Приклад:

Отже, – неповна частка,

–остача.

Тобто

Подільність многочленів. Дільники. Спільні дільники. Алгоритм Евкліда знаходження нсд двох многочленів.

Враховуючи наведену у попередньому параграфі теорему про ділення многочленів з остачею, можна отримати відповідь на питання, коли частка двох многочленів є знову многочленом.

Очевидно, що частка двох многочленів та,, буде многочленом т. і. т. т., коли остача від діленнянарівна нулю.

Означення та властивості подільності многочленів

Означ.1. Кажуть, що многочлен ділиться на многочлен, якщо існує многочлентакий, що

, (1)

У цьому випадку називають дільником многочлена, а–часткою від діленняна.

Позначення: ділиться на.

Доведемо тепер деякі властивості подільності многочленів.

Властивість 1. Нульовий многочлен ділиться на довільний ненульовий

многочлен:

Дійсно,

Властивість 2. Якщо то остача від діленняна

рівна нулю,

Дійсно,

.

Наслідок: Якщо остача від ділення многочлена нарівна нулю,

то

Властивість 3. Якщо і, то .

Дійсно,

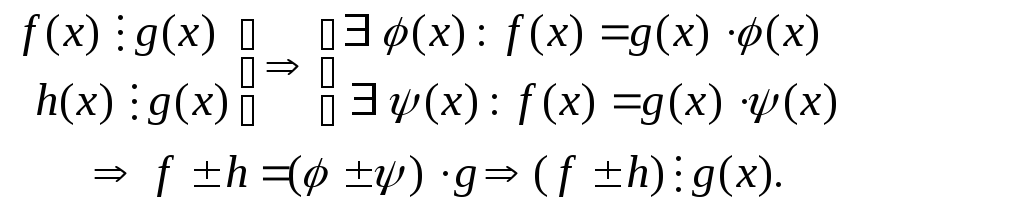
Властивість 4. Якщо многочлени , то для

довільних

Тобто лінійна комбінація многочленів, які діляться на , теж діляться на.

Дійсно,

Тоді

Властивість 5. Якщо то , добуток

Дійсно,

Властивість 6. Якщо

………..……

то для довільних многочленів , сума

Доведення випливає з властивості 4 та 5.

Властивість 7. Довільний многочлен ділиться на будь-який ненульовий

многочлен нульового степеня .

Дійсно,

Властивість 8. Якщо то

Дійсно,

.

Властивість 9. Якщо і, то.

Дійсно,

Перемножимо ці рівності

многочлен нульового степеня, .

Наслідок: Якщо , то.

Властивість 10. Якщо , то множина всіх дільників многочлена, які мають такий же степінь, як і, вичерпується множиною