10. Мінімізація логічних функцій.
Під мінімізацією ФАЛ розуміють перетворення її алгебраїчного виразу з метою отримання найпростішого виду функції. В інженерній практиці для мінімізації найширше застосування отримали наступні методи:
метод послідовного спрощення, що базується на застосуванні основних законів і тотожностей алгебри логіки;
метод, який базується на застосуванні карт Карно;
метод Квайна-Мак-Класкі.
При застосуванні метода карт Карно проводиться накриття карти за допомогою правильних конфігурацій, що містять нулі або одиниці (див. рис. 8). Правильними конфігураціями на карті Карно для функції алгебри логіки з n-змінними є всі прямокутники (горизонтальні, вертикальні, квадрати), які мають площу 2n-i (i = 0, 1, 2 …, n).
При накриванні ФАЛ стараються, щоб кількість накриттів на карті була мінімальною, а площа, що накривається кожною з правильних конфігурацій була максимальною. Конфігурації можуть перекриватись, накладатись одна на одну. При виборі накриття можливе об’єднання крайніх полів, що розміщені на крайніх протилежних сторонах карти в горизонтальному або вертикальному напрямках. Принцип мінімізації полягає в об’єднанні сусідніх полів карти в межах правильних конфігурацій. При знаходженні мінімальної форми ФАЛ виписуються усі змінні, які не змінюють свого значення в межах правильної конфігурації.
При об’єднанні полів, в яких записані одиниці функція алгебри логіки пишеться в диз’юнктивній нормальній формі, тобто у виді диз’юнкцій добутків змінних, які незмінні в межах кожної конфігурації накриття. При об’єднанні полів, що містять нулі, ФАЛ записується в кон’юнктивній нормальній формі, тобто у виді добутків диз’юнкцій інверсних значень змінних, які не змінюються при переході з одного поля конфігурації на інше. Приклади мінімізації декількох ФАЛ методом карт Карно наведені на рис. 8.
Рисунок 8. Приклади мінімізації функцій алгебри логіки методом карт Карно
11.Тригер Шмідта.
Тригер Шмідта - це специфічний вид тригера, що має один вхід і один вихід. Такий тригер
називають несиметричним. В тригері Шмідта перехід з одного стійкого стану в інший
здійснюється при певних рівнях вхідної напруги, званих пороговими рівнями. Тригер Шмідта
зображений нижче
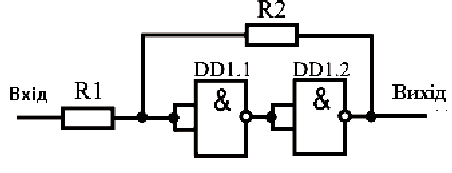
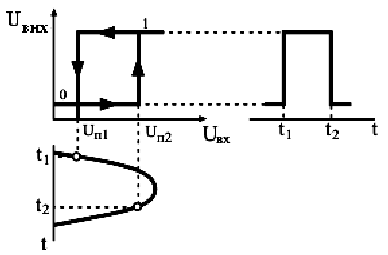
Рис.8.Тригер Шмідта і графіки, що пояснюють принцип його роботи
Якщо на вхід тригера Шмідта подавати наростаючу напругу (нижній графік), то при деякому
рівні (порозі) Uп1 у момент t1 напруга на виході стрибком переходить із стану 0 в стан 1. Якщо
зменшувати напругу на вході до деякої напруги Uп2 у момент t2 напруга на виході стрибком
переходить із стану 1 в стан 0. Явище неспівпадання рівнів Uп1 і Uп2 називається гістерезисом.
Відповідно, передавальна характеристика тригера Шмідта володіє гістерезисним характером.
Тригер Шмідта, на відміну від інших тригерів, не володіє пам'яттю і використовується для
формування прямокутних імпульсів з напруги довільної форми.
Тригери використовуються досить широко як самостійні пристрої, так і як основа для
складніших пристроїв - лічильників, регістрів, запамятовуючих пристроїв.