4.6.2.1Характеристики вільних згасаючих коливань

Вільні згасаючі коливання мають своїми характеристиками

• час релаксації,

• кількість повних коливань за час релаксації.

• декремент згасання,

• логарифмічний декремент згасання,

• добротність коливальної системи,

Час релаксації   це час, за який амплітуда коливання зменшується в е раз

_o(t) = Aexp(-t) 

e = _o(t) / _o(t+)= exp() 

 = 1/. (1)

За час релаксації система здійснить N_e=/T=1/(T) повних коливань.

Декремент згасання за визначенням є відношення амплітуд через період

,

а логарифмічний декремент згасання за визначенням є

і в іншому виді .

Енергію коливальної системи можна знайти на прикладі пружинного маятника масою m із сталою пружності k. Нехай його згасаючі коливання описуються функцією

,

де . Повна енергія маятника в кожний момент часу визначається амплітудою

,

зокрема, для t = 0 . В довільний час t потенціальна енергія

,

а кінетична енергія

.

У випадку фізичного маятника потрібно в одержаних результатах замінити х₀(t) на _o(t), а масу маятника m на момент інерції J.

Добротність коливальної системи за визначенням є

,

де E(t)  енергія системи в час t,  робота системи проти сил опору за період Т. Прийнявши до уваги, що енергія пропорційна квадрату амплітуди, можемо записати вираз для добротності у вигляді:



.

Для малих сил опору <<1 і з достатньою точністю можна записати:

.

Тепер добротність коливальної системи з незначними силами опору можна записати у такий спосіб:

Q=.

4.6.3. Вимушені коливання

Вимушені коливання маятника  це коливання, які відбуваються під дією зовнішньої періодичної сили. Для фізичного маятника це може бути сила, що створює момент сили , де  амплітуда і  частота. Рівняння вимушених коливань для періодичної змушучої сили має вигляд:

. (1)

Розв'язок рівняння (1) можна знайти з розв'язку іншого рівняння, а саме

, (2)

де  є дійсною частиною комплексної функції часу х(t)=(t)+іy(t):  = Re(x).

Розв'язок рівняння (2) шукаємо у вигляді комплексної функції(див.Додаток). Знайдемо похідні від х по t

. (3)

Зробимо підстановку (3) в (2)

. (4)

Множник при А у лівій частині (4) позначимо через Z і представимо в експоненціальному вигляді (див.Додаток)

, (5)

де - модульZ,  аргумент Z. Таким чином сталу А з (4) можна записати через Z у вигляді:

, (6)

а шукана функція х(t) буде такою

. (7)

З (7) знаходимо розв'язок рівняння коливань фізичного маятника у вигляді

,

де амплітуда коливань

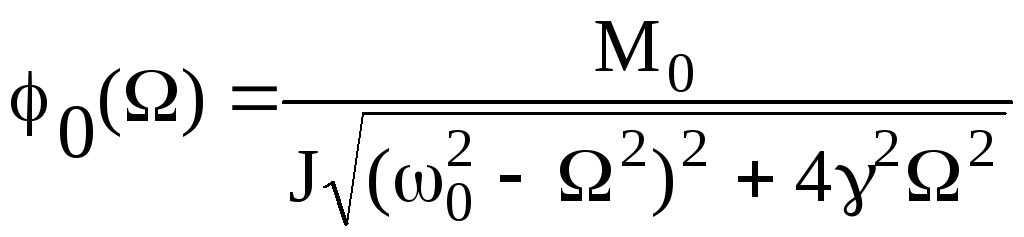(8)

є функцією частоти  примусової сили. Ця функція має максимум в точці _max , яка відповідає точці мінімуму квадрата модуля числа Z:

. (9)

Похідна від ² дорівнює

. (10)

Положення максимуму функції (_max) знайдемо, прирівнявши похідну від ² в точці _max нулю

. (11)

Механічний резонансявище різкого зростання амплітуди вимушених коливань (див. Мал.37), коли частота змушуючої силинаближається до резонансної частоти_рез.

Механічний резонанс для швидкості  явище різкого зростання амплітуди швидкості вимушених коливань. Можна показати що це явище наступає тоді, коли частота зовнішньої сили  наближається до резонансної .

Загальним розв'язком неоднорідного диференціального рівняння коливань є сума загального розв'язку однорідного рівняння та частинного розв'язку неоднорідного рівняння

. (12)

Через час t, більший часу релаксації , за рахунок експоненціального згасання, першим доданком в (12) можна знехтувати й вважати, що встановилися вимушені коливання.

. (13)