9.15. Електростатичне поле в діелектрикові

Якщо діелектрик помістити у зовнішнє електричне поле з напруженістю , то в ньому буде індукуватися внутрішнє поле(див.Мал.18), створене орієнтацією зв'язаних зарядів молекули: електрони атомів розмістяться назустріч полю, а ядра за полем. Сумарне поле буде мати напруженість . Можна показати, що в ізотропних діелектриках

,

де  безрозмірна величина, яка називається діелектричною проникливістю.

Дійсно, розглянемо поле в діелектрикові, що знаходиться між двома нескінченно великими різнойменно зарядженими пластинами площеюS і поверхневою густиною заряду (див.Мал.89). Напруженість полянаправлена в напрямкові протилежному векторуй величина результуючої напруженості. Напруженість поля між двома різнойменно зарядженими паралельними пластинами є

,, (1)

де  поверхнева густина зв'язаних зарядів діелектрика. Дипольний момент діелектрика дорівнює ,d  відстань між пластинами. Величина вектора поляризації діелектрика

. (2)

З іншого боку,

.

Порівнюючи наведені вирази для Р, знайдемо, що

. (3)

Таким чином остаточно маємо

Е = Е₀ - Е' = Е₀ - Е

і

, (4)

Що й треба було довести.

9.16. Індукція електростатичного поля . Теорема Остроградського-Гауса для індукції

Для характеристики деяких властивостей електричного поля вводиться поняття електричного зміщення (індукції) електричного поля . За визначенням у вакуумі

, (1)

в ізотропному діелектрику

. (2)

Теорема Остроградського-Гауса для електричного зміщення є

, (3)

де q  алгебраїчна сума вільних зарядів, що містяться усередині замкненої поверхні діелектрика S. Цей результат можна одержати, якщо в теоремі Остроградського-Гауса для напруженості поля, поряд із вільними, врахувати зв'язані заряди поляризованих молекул, розташованих на поверхні діелектрика з поверхневою густиною. Усередині діелектрика зв'язані заряди молекул взаємно компенсуються. Запишемо тепер теорему Остроградського-Гауса для напруженості у вигляді

. (3)

Тепер

(4)

і остаточно одержимо

.

9.17. Граничні умови для електричного поля в діелектрику

Граничні умови для електричного поля при переході границі двох діелектриків із діелектричними проникливостями ₁ та ₂ мають вигляд

. (1)

Індекс означає тангенціальну складову до граничної поверхні, а індекс нормальну складову відповідного вектора.

Для доведення цих співвідношень скористаємося виразами для циркуляції напруженості полята теоремою Остроградського-Гаусадля індукції. Врахуємо також, що в діелектрику відсутні в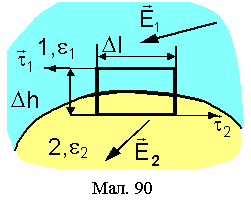ільні заряди і їх струм

q=0, j=0,

а зв'язок величин напруженості Е та індукції D має вигляд .

1. Умови, що виникають із циркуляції напруженості поля. Розглянемо контур, який охоплює ділянку границі розділу двох діелектриків у вигляді прямокутника з основою, що лежить на дотичній () та бічною стороною , денормаль до (див.Мал.90). Обхід контуру при інтегруванні будемо робити в напрямі проти годинникової стрілки. Спрямуємо h до 0 так, щоб верхня основа залишалась в діелектрику 1, а нижня в діелектрику 2. При цьому границя інтеграла від по бічній стороні буде рівна нулю. На верхній основі обхід контуру проти годинникової стрілки буде в напрямкуі

.

На нижній основі

(обхід контуру в напрямку проти ). Тепер інтеграл по замкненому контуру буде мати відмінними від нуля складові по основам Δl, які можна записати так

Звідси слідує перша пара граничних співвідношень

. (2)

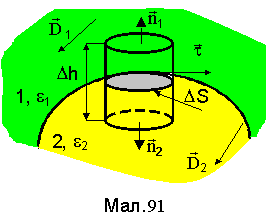
2. Умови, що виникають із теореми Остроградського-Гауса.

Для одержання другої пари умов на границі розподілу двох діелектриків побудуємо прямий до поверхні границі циліндр з основою та висотою (див.Мал.91). Інтеграл по замкненій поверхні цього циліндра відбуде мати лише дві складові по поверхні основ циліндра, якщо його твірну спрямувати до 0 так, щоб нижня основа залишилась в діелектрику 2, а верхня в 1. Крім того,діелектрик не містить вільних зарядів, тому в об'ємі циліндра q=0. Нормалі до нижньої та верхньої основ протилежні за напрямком На нижній основі

,

а на верхній основі

В підсумку маємо

і друга пара умов має вигляд

. (3)