9.12.Потенціал поля нескінченно великої зарядженої площини.

Нехай вісь Ох  нескінченно великій зарядженій площині з поверхневою густиною заряду . Для знаходження різниці потенціалів між точками, що знаходяться на відстанях х₁ та х₂ від площини з , скористаємося зв'язком напруженості та потенціалу поля

. (8)

Обчислюючи , ми зважили на те, що Ох і , де кут між векторами напруженості та переміщення(див.Мал.85 а).

Якщо поле створюється двома паралельними різнойменно зарядженими площинами, то різниця потенціалів усередині між площинами визначається також виразом (8) із відповідним значенням величини Е (див.Мал.85б).

9.13. Напруженість поля зарядженого циліндра та його потенціал

Визначення. Якщо точка знаходиться від циліндра на відстані значно меншій ніж лінійні розміри циліндра, то циліндр називається нескінченно довгим по відношенню до даної точки. При цьому розуміємо, що дана точка знаходиться також достатньо віддалено від кінців циліндра.

Напруженість поля нескінченно довгого зарядженого циліндра (див.Мал.86) із радіусом основи r та лінійною густиною заряду направлена по нормалі до бічної поверхні циліндра, бо в противному тангенціальна складова напруженості була б відмінна від 0 і по поверхні відбувався б рух зарядів, що суперечить закону збереження енергії. При R > r величина напруженості дорівнює

. (1)

Для доведення (1), побудуємо на осі циліндра другий проміжний циліндр, що охоплює перший, із твірною l і радіусом основи R>r. На поверхні основи проміжного циліндра нормаль до неї , а на бічній поверхні. Таким чином інтеграл по замкненій поверхні проміжного циліндра має відмінною від нуля складову по бічній поверхніі потік

. (2)

Усередині проміжного циліндра знаходиться заряд і за теоремою Гауса-Остроградського

Ф = =. (3)

Прирівнюючи вирази для Ф з (2) й (3), маємо й остаточно

.

Потенціал поля нескінченно великого зарядженого циліндра. Розглянемо нескінченно довгий рівномірно заряджений циліндр радіуса R із лінійною густиною заряду  (див.Мал.87). Зважаючи на те, що вектор направлений уздовж радіальних прямих циліндра, можна записати, де  кут між векторами та(див.Мал.16), та, різницю потенціалів між точками, що знаходяться на відстаняхтавід осі циліндра (), можна записати у вигляді

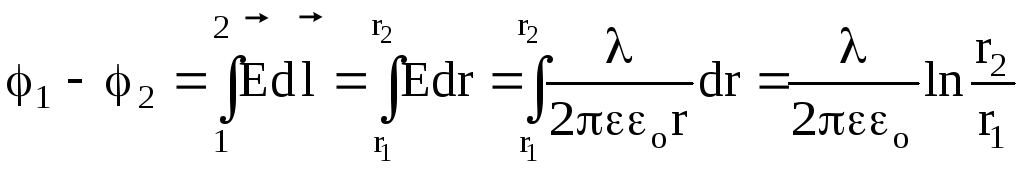. (4)

Якщо розглядаються два співвісні різнойменно заряджені металеві циліндри з радіусами та, то в просторі між ними поле створюється лише зарядом внутрішнього циліндра з напруженістю

,

а різниця потенціалів між поверхнями циліндрів становить

. (5)

Якщо , то

і

. (6)

Цей результат збігається з випадком для різниці потенціалів для двох різнойменно заряджених нескінченних площин.

9.14. Напруженість поля зарядженої сфери та її потенціал

Напруженість поля зарядженої сфери радіуса r, що містить заряд q, для R>r направлена по радіальним прямим (див.Мал.88) і за величиною дорівнює

. (1)

Для доведення цього результату розглянемо сферу радіуса R>r, центр якої співпадає з центром зарядженої сфери. Нормаль до сфери направлена по радіальній прямій і співпадає з напрямком напруженості поля (тангенціальна складова відсутня), тому =const на всій поверхні сфери. Запишемо потік напруженості

. (2)

За теоремою Остроградського-Гаусса

і остаточно маємо

E = ,

що й треба було довести. Цей результат збігається з напруженістю поля точкового заряду з тої причини, що задача має сферичну симетрію розподілу макроскопічного заряду.

Потенціал зарядженої сфери. Потенціал зарядженої сфери радіуса R із зарядом Q на відстані від центра r  R дорівнює

. (3)

Різниця потенціалів між точками, що знаходяться на відстанях r₁ та r₂ від центра дорівнює

. (4)

Поле двох різнойменно заряджених сфер із радіусами r та R>r й зарядом Q створюється лише внутрішньою сферою, а тому різниця потенціалів між сферами дорівнює

. (5)

Якщо , то

і

=. (6)

Цей результат також збігається з випадком для різниці потенціалів для двох різнойменно заряджених нескінченних площин.