9.21. Електрична енергія заряджених провідників. Енергія електростатичного поля

9.21.1. Електрична енергія відокремленого зарядженого провідника.

Електрична енергія відокремленого зарядженого провідника дорівнює

W_е=. (1)

Доведемо це твердження. Нехай на провідник нанесено заряд q. Він створить на поверхні провідника потенціал . Для збільшення заряду на провіднику на величину dq потрібно виконати роботу

. (2)

Ця робота йде на приріст потенціальної енергії провідника W i A=dW. Прирівнюючи вирази для роботи, одержимо

або . (3)

9.21.2. Енергія системи з N нерухомих точкових зарядів

Енергія системи з двох точкових зарядів і, відстань між якими становить, є енергія взаємодії одного заряду з другим і може бути записана як енергія одного заряду в полі другого так

,

тобто енергії взаємодії рівні між собою і дорівнюють енергії системи

.

Аналогічно можна розглянути систему з трьох і більше зарядів, враховуючи їх попарну взаємодію (принцип суперпозиції), і тоді

.

9.21.3. Енергія конденсатора.

Електрична енергія, наприклад, плоского конденсатора є сумою енергії двох різнойменно заряджених обкладинок

W = W₁ + W₂ = = = , (6)

де U=₁-₂.

Енергія циліндричного та сферичного конденсаторів має такий само вигляд як і для плоского.

9.21.4. Сила тяжіння між пластинами зарядженого конденсатора.

Потенціальну енергію зарядженого плоского конденсатора можна представити у вигляді функції х

, (7)

де х  відстань між пластинами. Величину сили взаємодії між пластинами знайдемо через градієнт потенціальної енергії

. (8)

9.21.5. Енергія електростатичного поля.

У зв'язку з тим, що електричне поле, наприклад, плоского конденсатора існує лише у обмеженому просторі  об'ємові конденсатора, тому можна вважати, що енергія зарядженого конденсатора тотожна енергії електричного поля

. (9)

Густина енергії електричного поля дорівнює

. (10)

w= =, (11)

де  напруженість, а  електричне зміщення поля.

Об'ємна густина енергії поляризації діелектрика може бути знайдена шляхом віднімання від об'ємної густини електричної енергії поля у діелектрику об'ємної густини електричної енергії поля у вакуумі при рівних напруженостях Е

, (12)

і остаточно

, (13)

де  вектор поляризації діелектрика.

9.22. Процес релаксації у контурі з ємністю

Р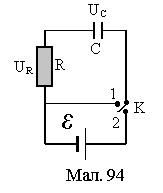озглянемо електричний контур з омічним опоромR та ємністю С (див. Мал.94). Залежність величини заряду q від часу t при зарядці й розряді конденсатора визначається величиною ємності С. Знайдемо цю залежність. При замиканні ключа К на контакт 2, конденсатор почне заряджатися. За законом Ома ІR + U_c =. Зважаючи, щоU_c = q/C та І = dq/dt, одержимо диференціальне рівняння

. (1)

Розв'язком (1) є сума загального розв'язку однорідного рівняння

(2)

та частинного розв'язку неоднорідного рівняння

. (3)

Розділивши в (2) змінні, одержимо

. (4)

Після інтегрування одержимо

,

або

. (5)

Частинний розв'язок (3) шукаємо у вигляді q=В і після підстановки одержимо , деq₀ є максимальний заряд конденсатора при електрорушійній силі Е. Остаточно розв'язок рівняння буде мати вигляд

. (6)

Якщо в момент часу t=0 і q=0, то стала A=-q₀ і після нескладних перетворень одержимо

. (7)

Якщо в момент часу t=0 конденсатора мав заряд q=q₀ при вимкненій електрорушійній силі (ключ К перемкнуто на контакт 1 і=0), то розв'язок буде мати вигляд

. (8)

Після підстановки початкових значень знайдемо, що стала А=q₀ і тоді

. (9)

Час  за який величина заряду зменшиться в е раз називається часом релаксації. Обчислимо величину . За визначенням маємо

(10)

і звідси

 = RC. (11)

Дайте визначення

Наведіть формули для визначення

Виведіть рівняння

Визначіть

Запишіть рівняння

Виведіть рівняння

Виведіть формулу

Знайдіть положення