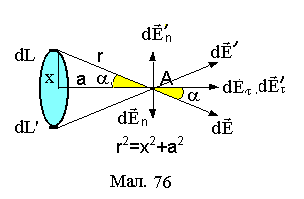
9.6. Напруженість електричного поля на осі зарядженого кільця

Виділимо на диску кільце радіуса х, як показано на Мал.76. Приймемо, що заряд Q рівномірно розподілений на площині диска з поверхневою густиною , а кільце диска містить зарядq із лінійною густиною . Напруженість dE, створювана елементом кільця dL із зарядом , дорівнює

, (19)

 де  відстань точки А від елемента кільця товщиною dL. Для обчислення напруженості поля кільця, необхідно скласти від усіх елементів кільцяdL. В цій сумі буде присутня складова напруженості від симетричного відносно центра елемента кільцяdL'. Вектори таможна розкласти на тангенціальні,та нормальні, складові. Нормальні складові напруженостей елементів dL та dL' , як рівні за величиною та протилежні за напрямком взаємно знищаться, а величина суми тангенціальних складових дасть величину напруженості поля кільця

. (20)

Тангенціальна складова напруженості така

. (21)

Підставивши (21) у вираз (20), обчислимо напруженість поля кільця

. (22)

9.7. Напруженість електричного поля на осі диска

Покладемо, що кільце має товщину dx і площу . Запишемо заряд кільцяq через поверхневу густину 

dQ=q=2xdx.

Тепер напруженість (14), створювану кільцем, як елементом диска, представимо у вигляді

. (23)

Для знаходження напруженості в точці А, створюваної зарядженим диском, необхідно проінтегруватиdЕ(х) по х від 0 до R

. (24)

Для обчислення інтеграла, зробимо заміну змінної

, 2xdx=dy,

при x=R

,

при x=0

.

Тепер обчислимо інтеграл

Остаточно величина напруженості поля диска на осі дорівнює

, (25)

де .

9.8. Електричний диполь та його поле

Якщо система з двох різнойменних точкових зарядів величиною q, відстань між якими l, розглядається на відстані r>>l, то вона називається диполем. Величина l  плече диполя. Диполь характеризується вектором дипольного моменту , направленим від від'ємного заряду до додатного.

Важливість розгляду електричного поля диполя зумовлюється тим, що природні джерела електромагнітного випромінювання можна моделювати електричним диполем. Така модель може достатньо точно описати енергію джерел як функцію просторових координат та часу.

9.8.1. Потенціал електричного поля диполя

Знайдемо потенціал та напруженість електричного поля диполя в точці А з радіус-вектором відносно середини плеча диполя О та кутом міжта моментом(див. Мал.77). Потенціал системи двох точкових зарядів у точці А дорівнює алгебраїчній сумі потенціалів, створених кожним із зарядів

,

,

Ми поклали, що , боr >> l. Тепер

= , або , (1)

9.8.2. Напруженість електричного поля диполя

Напруженість поля визначимо через потенціал (1) за формулою . Можна ввести таку систему координат, в якій указана формула є достатньо простою. Такою системою координат є система базисних ортонормованих векторів та . Вектор направлений у сторону зростання кута . Оператор у цих координатах має складовими

,. (2)

Відповідні компоненти напруженості (2) запишуться у вигляді

,. (3)

Продиференціювавши  із (1) по відповідним змінним, одержимо

,. (4)

Величину напруженості Е знайдемо з виразу

або

. (5)

Напруженість у точках на прямій, на якій лежить диполь (= 0 або=) дорівнює

, (6)

а в точці, що знаходиться на осі диполя ()

. (7)