9.19. Електроємність провідників

1. Електроємність відокремленого провідника. Відокремлений провідник, тобто такий, що не взаємодіє з іншими зарядженими тілами, має потенціал  пропорційний розміщеному на ньому зарядові q і тому можна записати, що q=C. Коефіцієнт пропорційності С називають електроємністю відокремленого провідника. Електроємність С залежить від геометричної форми та розмірів провідника. Розмірність електроємності [C]=В/м=Фарад, або скорочено [С]=Ф. Наприклад, електроємність відокремленого провідника, що є сферою з радіусом R дорівнює

. (1)

З цього виразу можна визначити розмірність електричної сталої []=Ф/м. Електроємність кулі, що має радіус рівний радіусу Землі R_З = 6,410⁶м, дорівнює С_З = 712 Ф.

2. Взаємна електроємність. Взаємна електроємність С двох різнойменно заряджених провідників із величиною заряду q визначається як , де₁ і ₂  потенціали провідників. Ємність С залежить від геометричної форми провідників та їх взаємного розташування.

Зауваження.Названі провідники можуть взаємодіяти з іншими зарядженими тілами, а їх електричне поле діє у навколишньому просторі.

9.20. Конденсатори

Конденсатором називається така система з двох різнойменно заряджених провідників з однаковою величиною заряду q, електростатичне поле якої зосереджується в обмеженому просторі між провідниками. Самі провідники називають обкладками конденсатора. До таких провідників можна віднести

• дві паралельні нескінченно великі площини  плоский конденсатор;

• два коаксіальні циліндри з близькими значеннями радіусів основ  циліндричний конденсатор;

• дві сфери зі співпадаючими центрами та близькими значеннями радіусів  сферичний конденсатор.

За визначенням електроємність конденсатора є

, (2)

де  потенціали провідників, U  різниця потенціалів.

1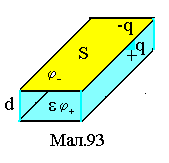. Плоский конденсатор утворюється двома металевими пластинами (обкладки конденсатора) площею S із відстанню d між ними, причому d<< лінійних розмірів пластин (див.Мал.93). Електростатичне поле пластин зосереджується усередині між ними. Між пластинами може розміщуватися діелектрик із діелектричною проникливістю . Електроємність плоского конденсатора становить

С = . (3)

Дійсно, напруженість поля між пластинами , різниця потенціалівU=₁ - ₂=Ed, q=S і остаточно маємо

С = =.

2. Циліндричний конденсатор складається з двох співвісних металічних тонкостінних циліндрів (обкладок конденсатора) висоти h і радіусів R₁ та R₂, причому h >> R₁, R₂. Електростатичне поле зосереджується усередині конденсатора й утворюється лише внутрішньою обкладкою. Електроємність циліндричного конденсатора можна розрахувати так:

, (4)

. (5)

Якщо d=R₁ - R₂ <<R₁, то ln (R₁ / R₂)=ln(1+d/R₁)d/R₁ і тоді вираз для ємності циліндричного конденсатора приймає вид ємності плоского конденсатора

С=,

де S = 2hR₁  бічна поверхня циліндра.

3. Сферичний конденсатор складається з двох концентричних металічних тонкостінних сфер (обкладок конденсатора) радіусів R₁ та R₂. Електростатичне поле зосереджується усередині конденсатора й утворюється лише зарядом внутрішньої сфери. Напруга між обкладками

U=kq. (6)

Електроємність сферичного конденсатора

С=q/U=4₀. (7)

Нехай R₂ - R₁ = d << R₁, R₂ і R₁ = R₂ = R. Площа поверхні сфери S = 4R² i тоді

С = . (8)

4. Системи з'єднаних конденсаторів.

При паралельному з'єднанні конденсаторів у батарею, їх загальна ємність дорівнює сумі ємностей усіх конденсаторів батареї. Дійсно, при такому з'єднанні сумарний заряд Q на обкладинках батареї конденсаторів дорівнює сумі зарядів на всіх конденсаторах Q =  q_i , а різниця потенціалів U буде однаковою як для батареї так і для кожного конденсатора окремо. Тепер

, (9)

що й треба було довести.

При послідовному з'єднанні конденсаторів у батарею величина обернена їх загальній ємності дорівнює сумі величин, обернених ємностям усіх конденсаторів батареї. Дійсно, при такому з'єднанні сумарна напруга на обкладинках батареї конденсаторів дорівнює сумі напруг на всіх конденсаторах U = , а зарядq буде однаковим як для батареї так і для кожного конденсатора окремо q_i=q. Тепер

= i , (10)

що й треба було довести.