10.7.2.Друге правило Кірхгофа

В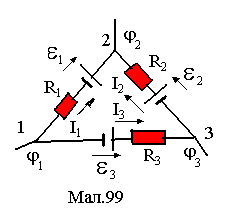розгалужених колах виділяються окремі замкнені контури, вершинами яких є вузли. Кожна зі сторін контуру розглядається як неоднорідна дільниця струму з потенціалами_і та _і+1, струмом І_і, опором R_і, електрорушійною силою Е_і та напругою U_і=R_іІ_і. За додатній прийнято напрямок обходу контуру проти годинникової стрілки, тобто напрямок 132 для прикладу, зображеного на малюнку 99. Виведемо 2-е правило Кірхгофа. Запишемо вирази для напруги на ділянках 1,2, 3 :

Якщо додати ліві та праві частини записаних рівностей, то в правій частині послідовно взаємознищуються потенціали  і в результаті одержимо 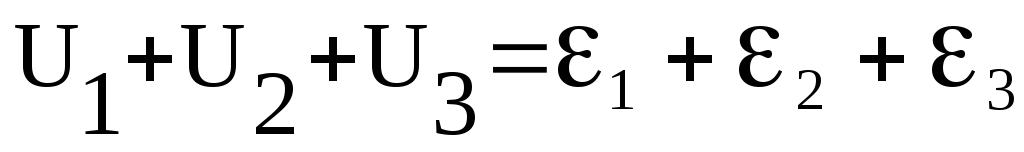. Одержана рівність

(2)

виражає друге правило Кірхгофа. В (2) напруги беруться із знаком "+", якщо відповідні їм струми за напрямком співпадають із напрямком обходу контуру, а в противному їм приписується знак "-". За додатній напрямок ЕРС береться напрямок від полюса "-" до полюса "+", як це показано на малюнкові. Знак ЕРС у правій частині (2) визначається співпаданням напрямку ЕРС із напрямком обходу (знак "+"), чи ні (знак"-"). За законом Ома U_і = І_іR_і і друге правило Кірхгофа можна записати також у вигляді

. (3)

10.7.3.Розв'язок електротехнічних задач на основі правил Кірхгофа.

Методика розв'язування цих задач полягає в тому, що в розгалужених колах виділяються вузли й окремі замкнені контури. Указується додатній напрям обходу контурів: проти годинникової стрілки. Далі визначаються струми та ЕРС і їх напрями на кожній зі сторін контуру. Знаки струмів та ЕРС додатні, якщо їх напрямки співпадають із напрямком обходу контуру. Для вузлів записують перше, а для контурів друге правило Кірхгофа. Таким чином можна одержати необхідну систему незалежних лінійних рівнянь відносно невідомих опорів R, струмів І та ЕРС.

10.8. Електропровідність рідин

Носіями струму в рідинах є іони. До таких рідин відносяться ті, що

мають вільні заряди  йони, утворені внаслідок дисоціації молекул. Під дисоціацією розуміють розпад під впливом розчинника молекули на додатній (аніон) та від'ємний (катіон) йони, які мають рівні за величиною заряди. Електролітична дисоціація відбувається при розчиненні кислоти, солі або лугу в результаті взаємодії молекул цих речовин із полярними молекулами води чи інших розчинників, які мають значний дипольний момент. Унаслідок хаотичного теплового руху іонів, відбувається також зворотний дисоціації процес  молізація, при якому знову утворюється нейтральна молекула. В умовах динамічної рівноваги дисоціації та молізації електроліт характеризується коефіцієнтом дисоціації , який дорівнює відношенню числа дисоційованих молекул до їх загального числа в розчині.

Як відомо, зв'язок іонних молекул між собою здійснюється через валентні електрони, число яких позначимо через Z. Ці електрони сприймаються одним чи декількома атомами в результаті чого одна з груп атомів стає додатнім іоном, а інша від'ємним іоном. Таким чином заряд іона можна записати у вигляді q=Ze, де . Через М позначимо молярну масу іона виражену в атомних одиницях маси.

При створенні в електроліті електричного поля напруженості Е, іони починають направлений упорядкований рух із дрейфовою швидкістю V, яка, як і в металах, пропорційна напруженості поля Е, причому , де знакивідносяться до додатних та від'ємних іонів відповідно, а їх рухливості. Вираз для густини струму можна записати у вигляді

, (1)

де n концентрація іонів,   провідність. Рухливість u_ у першому наближенні не залежить від напруженості поля, а визначається природою іона, температурою, в'язкістю та іншими характеристиками електроліту.

При проходженні струму І через електроліт відбувається перенос маси речовини. При цьому на електродах виділяється N іонів відповідної речовини із зарядом Q. Маса речовини пропорційна величині заряду Q=Іt=Nq=NZe, що пройшов за час t

. (2)

Якщо чисельник та знаменник помножити на число Авогадро N_a=6.02210²³ моль^-1, то в чисельнику одержимо молярну масу речовини

,

а в знаменнику універсальну сталу Фарадея

. (3)

Як видно з (3) число Фарадея F чисельно дорівнює заряду моля електронів. Тепер вираз для маси може бути записано у вигляді

.

Коефіцієнт к називається електрохімічним еквівалентом іона, а коефіцієнт k_х називається хімічним еквівалентом іона.