1.2. Символьні позначення приростів фізичних величин

В тексті прийняті такі позначення:

- символом  позначаються скінченні (у тому числі і малі) прирости скалярних та векторних фізичних величин;

- символом d позначаються нескінченно малі прирости скалярних та векторних фізичних величин, які є функціями стану тіла або системи тіл. Такі величини в математиці називають диференціалами. Вони утворюються як границя скінчених приростів  при прямуванні їхнього аргументу або самого  до 0. Основною властивістю нескінченно малої величини є те, що вона завжди менша будь-якої наперед заданої малої скінченої величини;

- символом  позначаються нескінченно малі (їх називають ще елементарними) значення фізичних величин, які не є функціями стану тіла або системи тіл, наприклад, А - елементарна робота, Q - елементарна теплота та інші фізичні величини.

1.3. Основні поняття та визначення механіки

1.3.1. Механічний рух

Механічний рух – процес переміщення одних тіл відносно інших в умовах дії на них неврівноважених сил. У процесі механічного руху відбувається зміна взаємного розташування тіл у часі і просторі. Мірою зміни взаємного розташування тіл у просторі (зміни радіус-вектора положення тіла ) є переміщення, а у часі – швидкість . Мірою зміни швидкості з часом є вектор прискорення тіла . Криволінійний рух завжди можна розкласти на прості рухи:поступальний та обертовий.

Будь-який криволінійний рух тіла можна розкласти на два простих: поступальний та обертовий.

П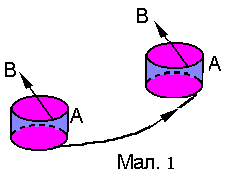оступальний рух - це рух, під час якого пряма АВ, проведена через дві точки тіла (див. Мал.1), залишається паралельною сама собі. При цьому всі точки тіла описують однакові траєкторії, вони мають однакові переміщення, шляхи, швидкості та прискорення. Таким чином, щоб описати рух тіла, достатньо описати рух однієї з його точок.

Обертовий рух - це рух, під час якого кожна точка тіла рухається по колу, центри яких лежать на одній прямій. Вона називається віссю обертання. Вісь обертання перпендикулярна площині обертання точок і може проходити через тіло або знаходитися поза ним. При обертальному русі всі точки мають однакові кутові швидкості та кутові прискорення.

1.3.2.Фізичні моделі тіла.

Матеріальна точка (МТ) – тіло, розмірами якого по відношенню до характерних відстаней у задачі можна знехтувати. Матеріальна точка — це модель реального тіла, що має три властивості:

— не має розмірів;

— має масу;

— матеріальні точки взаємно непроникні.

В одну геометричну точку простору можна помістити лише одну матеріальну точку. Матеріальна точка уведена фізиками для спрощення розрахунків при рішенні багатьох задач.

Абсолютно тверде тіло (АТТ) - тіло, зміною розмірів та форми (деформаціями) якого при умовах даної задачі можна знехтувати.

Абсолютно пружне тіло- тіло, деформації якого пропорційні діючим на нього зовнішнім силам і зникають, після припинення дії сил.

Абсолютно не пружне тіло- тіло, деформації якого повністю зберігаються, після припинення дії на нього зовнішніх сил.

1.3.3. Кінематичні характеристики механічного руху.

1. Траєкторія - геометричне місце точок простору, через які послідовно проходить матеріальна точка під час руху, або уявна крива S(t), яку описує точкове тіло під час руху (див. Мал. 2). В залежності від виду траєкторії розрізнюють прямолінійний (траєкторія є пряма) та криволінійний рух (траєкторія є деякою, у загальному випадку, просторовою кривою).

2. Початком відліку називається тіло або сукупність взаємно нерухомих тіл відносно яких розглядається переміщення інших тіл. З початком відліку, як правило, зв'язується початок системи координат.

Початок відліку, система координат та годинник, за яким проводиться відлік часу, утворюють систему відліку. Вибір тої або іншої системи відліку визначає відносність механічного руху.

Форма траєкторії та довжина траєкторії одного й того ж руху відносні. Вони залежать від вибору системи відліку. Щоб переконатися в цьому, проведіть олівцем на папері лінію; у системі відліку, зв'язаної з листом паперу, траєкторія кінчика олівця збігається з проведеною лінією, а в системі відліку, зв'язаної з кистю руки, кінчик олівця спочиває, його траєкторія виродилася в точку — і форма, і довжина траєкторії кінчика олівця в різних системах відліку виявилися різними.

3. Дотичною до траєкторії у точці А є граничне положення січної СВ (див. Мал. 2), коли точки С та В прямують до точки А. Напрямок дотичної можна задати одиничним вектором

.

Граничне положення площини, що містить точки А, В, С при прямуванні точок С та В до точки А визначає стичну площину. Площина, перпендикулярна стичній площині, у якій лежить одиничний вектор дотичної , називаєтьсядотичною площиною до траєкторії. Одиничний вектор , що лежить устичній площині і перпендикулярний до вектора , називаєтьсянормаллю до траєкторії.

4. Вектор , проведений з точкиО, яка є початком системи відліку, у точку А положення точкового тіла у просторі називається радіус-вектором. Радіус-вектор тіла, що рухається, є функцією часу, а рівняння

(1)

називають кінематичним рівнянням руху тіла. Лише вектор, що визначає положення тіла у просторі має приставку радіус-.

5. Якщо за час , тіло перемістилося з точки С у точку В, то вектор ,проведений з початкового положення тіла (точка С) у кінцеве положення (точка В), визначає зміну положення матеріальної точки за деякий проміжок часу і називається векторомпереміщення, або переміщенням. Вектор переміщення лежить на січній СВ. Коли точки В і С спрямляються до точки А, то вектор переміщення переходить у нескінченно малий вектор переміщення , який буде лежати на дотичній і його можна записати у вигляді=dr.

6. Одиничний вектор (модуль або величина вектора =1), що визначає деякий напрямок, називається ортом напрямку. Ортом дотичної до кривої є вектор і він називаєтьсятангенціальним, а орт називається ортомнормалі.

Будь-який вектор можна розкласти на нормальну та тангенціальну складові. Для цього потрібно з початку і вершини вектора опустить на даний напрямок перпендикуляри. Наприклад, векторнаМал. 3 має тангенціальну та нормальнускладові, причому

. (3)

7. Радіусом кривизни траєкторії в точці В є радіусR дотичного до неї у цій точці кола, яке лежить у стичній площині. Дугою такого можна наблизити ділянку dS траєкторії АС (див. Мал. 4).

Центр такого кола О визначається точкою перетину нормалей до траєкторії у точках А та С, коли вони прямують до точки В. Радіус цього кола буде радіусом кривизни R. Величина, обернена до величини R

,

називається кривизною траєкторії в даній точці.

8. Годограф вектора-функції - крива S(t), що являє собою множину точок положення вершин радіус-вектора. Таким чином траєкторія тіла S(t) є годографом радіус-вектора . Скалярне рівняння

S=S(t), (4)

як і рівняння (2), є також кінематичним рівнянням механічного руху тіла.

9.Для кількісного (аналітичного) опису механічного руху тіл у просторі вводяться системи координат (див. Мал. 5), початок відліку в яких зв'язується з початком системи відліку О. До таких систем відносяться Декартові з осями координат (x,y,z), сферична - (r,,), циліндрична - (z,r_,), полярна - (r,) та інші. Радіус-вектор у цих системах представляється через його координатні проекції, наприклад, в декартовій системі або, депроекції векторана осі координат. Вектори є взаємно перпендикулярні орти осей OX, OY, OZ відповідно.

Радіус-вектори положення тіла у двох різних системах відліку зв'язані між собою співвідношенням де— радіус-вектор у системі відлікуO, — радіус-вектор у системі відлікуO', - радіус-вектор системи відлікуO' відносно O (див.Мал.6).

В декартовій системі координат цей зв'язок має вигляд

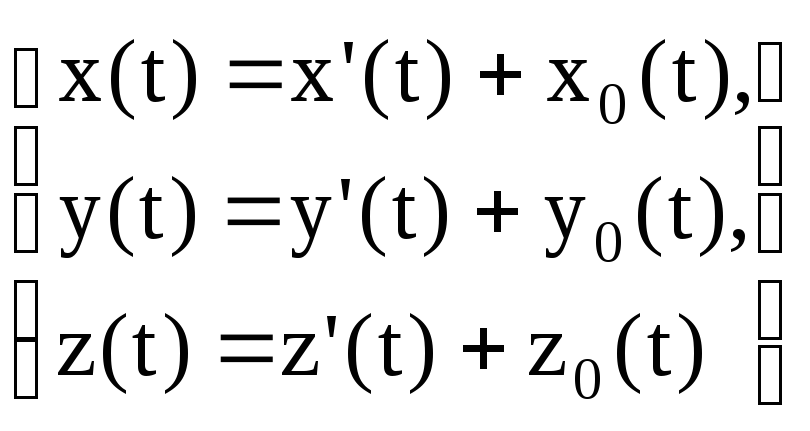, (5)

де індексом 0 позначені складові вектора . Приведені рівняння називають ще рівняннями перетворення координат Галілея.Вибір системи відліку визначається зручністю розвязку конкретної задачі.

10. Вектор переміщення є різницею радіус-векторів тіла

. (6)

Для нескінченно малого переміщення

. (7)

Переміщення та залежaть від вибору системи відліку, наприклад,переміщення у двох різних системах відліку зв'язані між собою співвідношенням , де— переміщення матеріальної точки в першій системі відліку,— переміщення матеріальної точки в другій системі відліку,- переміщення другої системи відліку відносно першої (див.Мал.6).

Закон незалежності рухів визначає, що у випадку, коли тіло приймає участь у декількох рухах, то результуюче переміщення є векторною сумою переміщень, здійснених тілом за той же проміжок часу у кожному з рухів, які здійснюються тілом нарізно.

Шлях, пройдений тілом dS(t), при переміщенні з точки А у точку В - довжина ділянки траєкторії , або відстань від точки А до точки В, виміряна вздовж траєкторії. Одиницею вимірювання величини шляху є м.