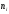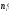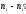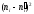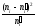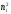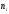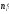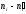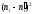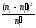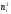6. Перевірка гіпотези про нормальний розподіл генеральних сукупностей X та y, використовуючи критерій погодженості Пірсона

Перевірка гіпотези про закон розподілу здійснюється за допомогою спеціально підібраної величини – критерію узгодженості.

Існує декілька критеріїв узгодженості: 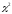, Колмогорова, Смірнова К. Пірсона, тощо.Для перевірки гіпотези про нормальний закон розподілу генеральної сукупності скористаємось критерієм Пірсона, перевагою якого є те, що він застосовується не тільки до нормального, але і до інших розподілів.

Для того, щоб при заданому рівні значущості перевірити нульову гіпотезуН₀: генеральна сукупність розподілена нормально, потрібно спочатку обчислити теоретичні частоти 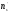, а потім значення критерію за даними вибірки:

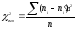
і за таблицею критичних точок 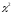(додаток 4), за заданим рівнем значущості і числом ступенів вільностіk=s-3 знайти критичну точку .

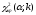Якщо 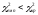– немає підстав відхилити нульову гіпотезу.

Якщо 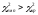– нульову гіпотезу відхиляють.

Обсяг вибірки повинен бути достатньо великим, принаймні не менше 50.

Отже, необхідно перевірити гіпотези про нормальний розподіл генеральних сукупностей X та Y, використовуючи критерій погодженості Пірсона.

При рівні значущост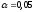і перевіримо гіпотезу про нормальний розподіл генеральної сукупності, якщо відомі емпіричні (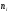) і теоретичні частоти

Для вибірки Х будуємо розрахункову таблицю (табл.13.)

Число ступенів вільності, зважаючи на те, що число груп вибірки (число різних варіант) s=6, k=s-3=6-3=3

Таблиця 13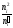

7	4,229	2,771	7,680	1,816	49	11,588
9	9,014	-0,014	0,000	0,000	81	8,986
11	12,573	-1,573	2,476	0,197	121	9,623
13	11,696	1,304	1,702	0,145	169	14,450
7	7,161	-0,161	0,026	0,004	49	6,842
3	0,791	2,209	4,879	6,168	9	11,377
∑=50	45,464			8,330		62,867

Обчислене значення критерію: χ²_емп = 8,330;

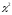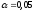За таблицею критичних точок (додаток 6)розподілу , за рівнем значущостіі числом ступенів вільностіk=3 знаходимо 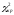(0,05;3)=7,8.

Як бачимо 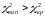, отже у нас є підстави відхилити нульову гіпотезу, тобто розходження емпіричних і теоретичних частот відчутне

Побудуємо розрахункову табл. 14 для вибірки Y:

Число ступенів вільності, зважаючи на те, що число груп вибірки (число різних варіант) s=7, k=s-3=7-3=4

Таблиця 14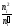

6	3,559	2,441	5,959	1,675	36	10,116
8	7,194	0,806	0,650	0,090	64	8,896
10	10,467	-0,467	0,218	0,021	100	9,554
10	11,132	-1,132	1,282	0,115	100	8,983
8	8,590	-0,590	0,348	0,041	64	7,451
5	4,853	0,147	0,022	0,004	25	5,152
3	1,121	1,879	3,530	3,149	9	8,027
∑=50	46,916			5,094		58,179

Отриманий результат: χ²_смп = 5,094;

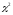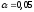За таблицею критичних точок (додаток 6) розподілу , за рівнем значущостіі числом ступенів вільностіk=4 знаходимо 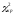(0,05;4)=9,5.

Тобто, обчислення виконані правильно.

Оскільки 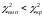– дані спостережень узгоджуються з гіпотезою про нормальний розподіл генеральної сукупності. Іншими словами, розходження емпіричних і теоретичних частот несуттєве.