6. Спектральный анализ непериодических сигналов. Преобразование Фурье. Равенство Парсеваля.

Преобразование Фурье

Преобразование Фурье является инструментом спектрального анализа непериодических сигналов. Для наглядной иллюстрации перехода от ряда Фурье к преобразованию Фурье, часто используют подход:

Представляем периодическую последовательность импульсов произвольного вида и сформировываем ряд Фурье для неё. Затем, не меняя формы одиночных импульсов увеличиваем период их повторения и снова рассчитываем коэффициент ряда Фурье.

Изменение пределов интегрирования не играет роли, ведь на добавленном пространстве сигнал имеет нулевое значение. Единственные дополнительное изменения будет состоять в уменьшении общего уровня гармоник из-за деления результата интегрирования на увеличившийся период Т.

На рис описаны изменения иллюстрирующиеся на примере двукратного увеличения периода следования прямоугольных импульсов.

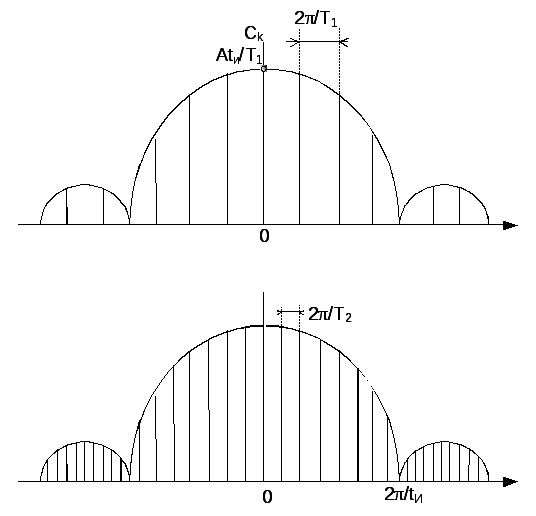
Вывод: С ростом периода следования импульса гармоники располагаются ближе друг к другу по частоте, а общий уровень спектральных составляющих становится всё меньше. При этом вид вычисляемого интеграла не меняется. Если устремить период к бесконечности(периодическая последовательность переходит в одиночный импульс) гармоники спектра будут плотно занимать всю частотную ось.

Однако взаимное соотношение между уровнем гармоник остаётся неизменным и определяется интегралом. Поэтому при спектральном анализе непериодических сигналов формула для расчёта коэффициентов комплексного ряда Фурье модифицируется так:

1 Частота перестаёт быть дискретно меняющийся и становится непрерывным параметром преобразования

2 удаляются множители 1/Т

3 Результатом вычислений вместо номерованных коэффициентов ряда Ск являются функция частоты S(w) – спектральная функция сигнала S(t).

В результате перечисленных модификаций наша формула переходит в формулу прямого преобразования Фурье

Перед интегралом появляется деление на 2П-обратное преобразование Фурье

Если использовать обычную частоту а не циклическую, то формула выглядит

Чтобы преобразование Фурье было применимо, сигнал должен удовлетворять требованиям:

1 Должно выполняться условие Дирехле

2 Сигнал должен быть абсолютно интегрируемый- интеграл от его модуля – конечная величина

Равенство Парсеваля

Равенство Парсеваля – соотношение позволяющее вычислить энергию сигнала как во временной так и в частотной области.

Оно утверждает, что энергия заключённая в импульсе равна сумме энергий всех составляющих его спектров.

Равенство Парсеваля характеризует важное свойство сигнала: если некоторая система пропускает только часть спектра сигнала, ослабляя другие её составляющие, то это означает что часть энергии сигнала теряется