
умк_Дегтярев_Геодезия_ч.1_2010г
.pdf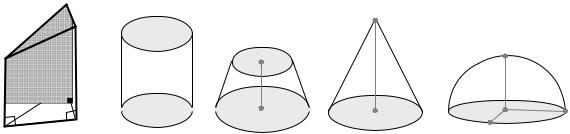
Н2 |
|
h |
S2 |
h |
|
|
Н1 |
|
c |
|
|||
|
h |
|
||||
Н3 |
|
|
|
a |
||
Sосн. |
Sосн. |
|
S1 |
Sосн. |
b |
|
а) |
б) |
|
в) |
г) |
д) |
|
Рис. 7.30. Элементарные объемные фигуры: а) прямоугольная призма; б) цилиндр; в) усеченный конус; г) конус; д) полуэллипсоид (полусфера)
Площади оснований могут быть получены с использованием палетки или механически.
При практической реализации определения объемов пространственных объектов на топографических планах выделяют следующие подходы:
–определение объема посредством деления объекта на элементарные фигуры с последующим их суммированием;
–определение объема путем разбивки объекта профилям;
–определение объема на основе сеточного моделирования.
При первом подходе, объемную фигуру, определенную по высоте горизонталями делят на ряд цилиндроподобных фигур с одинаковой высотой образующей h и площадями оснований Si (рис. 7.31, а). Тогда общий объем V определяется как сумма объемов Vi, определенных по формуле (7.23б). Так как высота образующей конуса, она же высота сечения рельефа h, для всей фигуры одинакова, то формулу обычно представляют в виде
V = h ·(S1 + S2 + …) + Vвер, |
(7.24) |
где Vвер – объем вершинной фигуры, которая может быть конусообразная, или эллипсоидообразная с формулами объема (7.23г), или (7.23д) соответственно.
Так как способ по форме весьма похож на численное дифференцирование методом прямоугольников, то его часто называют методом прямоугольников определения объемов.
Более точный способ при первом подходе можно получить, используя в качестве элементарных фигур усеченные конусообразные шаблоны (рис. 7.30, в, б). Теперь суммарный объем получают на основе формулы (7.23в), которыйиз-заравенствавысотысеченияможетбытьпредставленкак
V = 0.5· h ·(S1 + 2S2 + 2S3 + … + Sn) + Vвер. |
(7.25) |
Здесь Vвер определяется также как и в предыдущем случае. Этот способ часто называют методом трапеций.
341
V8 |
|
|
|
|
V8 |
|
|
|
V7 |
h |
|
|
|
V7 |
h |
|
|
V6 |
|
|
|
V6 |
|
|||
V5 |
|
|
|
|
V5 |
|
|
|
V4 |
|
|
|
|
V4 |
|
|
|
V3 |
|
|
|
|
V3 |
|
|
|
V2 |
|
|
|
|
V2 |
|
|
|
V1 |
|
|
|
V1 |
|
|
||
S6 |
S5 S4 S3 S2 |
S1 |
|
|
S6 |
S5 S4 S3 S2 |
S1 |
|
а) |
|
|
|
б) |
|
|
|
|
|
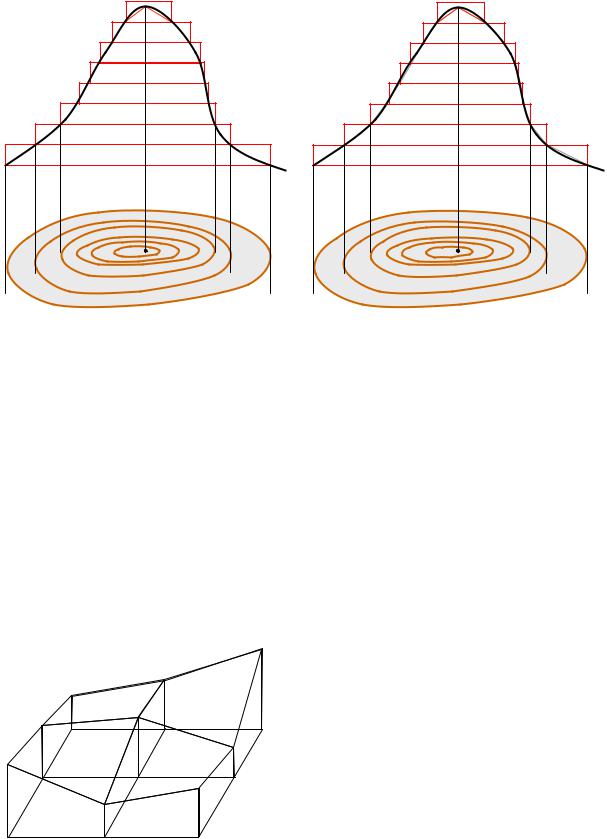
Рис. 7.31. Определение объемов фигур: |
|
|
|||||
а) методом прямоугольников; б) методом трапеций |
|
|||||||
При определении объемов по профилям используют аналоги формул |
||||||||
для прямоугольной призмы и усеченноконических фигур. Если площади |
||||||||
вертикальных сечений будут Si, а расстояние между ними d, то имеем |
||||||||
формулу |
|
|
|
|
|
|
|
|
|
V = d / 2 (S1 + 2S2 + S3 ), |
|
|
(7.26) |
||||
как частный случай для трех сечений и одинаковых расстояний между ни- |
||||||||
ми (рис. 7.32). |
|
|
|
|
|
|
|
|
При вычислении объемов на основе сеточного моделирования, уча- |
||||||||
сток, для которого вычисляется объем, делится на регулярные плоские фи- |
||||||||
|
|
|
гуры. В основном это квадраты или |
|||||
|
|
|
прямоугольные треугольники. За- |
|||||
S3 |
|
|
давшись высотой нижней горизон- |
|||||
|
|
тальной плоскости (в общем случае |
||||||
S2 |
|
d |
не |
обязательно |
горизонтальной, но |
|||
|
при |
наклонной |
сильно усложнится |
|||||
|
|
|||||||
S1 |
d |
|
алгоритм), всю задачу сводят к опре- |
|||||
|
делению объемов 3- или 4-угольных |
|||||||
Рис. 7.32. определение объемов |
прямоугольных призм на основании |
|||||||
формулы (7.23а) |
с |
последующим |
||||||
по профилям |
|
|||||||
|
суммированием (рис. 7.33). |
|
||||||
|
|
|
|
|||||
|
|
|
342 |
|
|
|
|
|
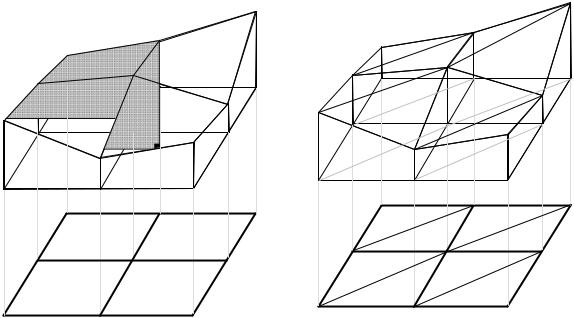
Проектировочные задачи, решаемые на планах. Под процедурой проектирования в самом общем смысле будем понимать процесс отображения графических элементов плана в графические элементы, преобразованные на основании каких-либо условий. Например, преобразовать участок реального рельефа, представленного горизонталями в наклонную плоскость с уклонами ix и iy при условии, что объем земляных масс над проектной плоскостью равен объему пустот под этой плоскостью (проектирование плоскостей с балансом земляных работ). Очевидно, что проектирование в такой трактовке основано на работе с графическими элементами: точками, линиями, плоскостями и телами. Чтобы отличать реальные элементы от проектных элементов, к проектным будем добавлять индекс «П»:
–для i-той точки (РП)i с проектными координатами (XП, YП, HП)i;
–для линии aП и т.д.
Исходя из перечисленных графических элементов, проектировочные задачи можно разделить на точечные, линейные, плоскостные и телесные. При этом следует учитывать, что преобразование может производится по следующим группам:
–реальные графические элементы в проектные элементы;
–проектные графические элементы в проектные элементы;
–получение каких-либо характеристик проектных графических эле-
ментов.
Из точечных проектировочных задач, исходя из того, что мы работаем с прямыми и плоскими графическими элементами, можно выделить следующие:
–получение высоты точки, которая находится на проектной линии на расстоянии S от её начала;
–получение высоты точки, которая находится на пересечении двух проектных (или проектной и реальной) линий;
–получение высоты точки, которая принадлежит проектной плоскости, заданной какими-либо элементами;
Решение всех задач напрямую зависит от того, каким образом задавались проектные графические элементы. Выделим три самых распространенных группы задания элементов:
1) точка задается парой своих координат в декартовой (x, y) или по-
лярной (α, d) системе;
2)линия задается или координатами двух её точек в любой системе, или координатами начала и ориентирным углом;
3)плоскость может быть задана или координатами трех её точек, или двумя пересекающимися линиями.
344

Очевидно, что это не все возможные варианты, а самые распространенные в геодезии.
При задании проектной линии двумя точками (XП, YП, HП)1 и (XП, YП, HП)2 решение первой точечной задачи может быть следующим: высота точки Н0, принадлежащая проектной линии (рис. 7.34), будет:
|
|
|
Н0 = Н1 + h1-0. |
(7.28) |
|
|
|
|
|
|
2 |
|
|
D |
0 |
h1-2 |
|
1 |
|
h1-0 |
|||
ν S |
|
|
|||
|
|
|
|
|
|
S0
Рис. 7.34. Решение первой точечной задачи проектирования
Превышение h вычисляется в зависимости от того, какая длина, наклонная D или горизонтальное проложение S, задано и какие элементы вычислить проще. Возможная последовательность:
1) вычислить по приращениям общее горизонтальное проложение S0, если оно не задано;
2) вычислить уклон (или тангенс угла наклона) по высотам точек 1 и 2 и общему горизонтальному проложению S0:
i = tan(ν) = H2 − H1 .
S0
3) зная горизонтальное проложение S до точки 0, вычисляем требуемое превышение как h = i · S. Если задано наклонное расстояние D, то проще привести его к горизонту через известный уклон, например, как
S = D
1+i2
и опять воспользоваться определенной выше формулой для превышения. Следует иметь ввиду, что если точка 0 – середина линии 1-2, то её
высота равна средней высоте вершин линии. Более общий подход на этой основе (то есть через обычную пропорцию) можно представить как
(рис. 7.34):
h1−2 |
= |
h1−0 |
h |
= h |
|
D |
. |
(7.29) |
D |
D |
|
||||||
|
1−0 |
1−2 |
|
D |
|
|||
1−2 |
|
|
|
|
|
1−2 |
|
|
345
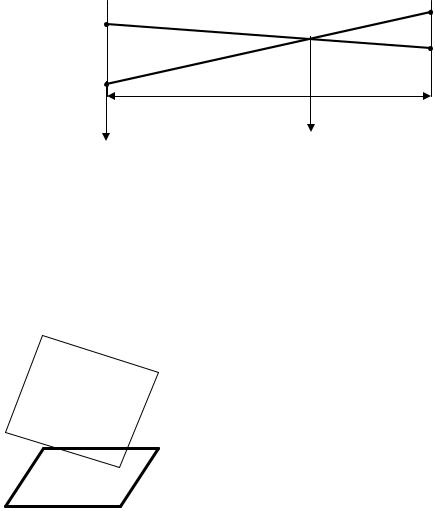
При решении второй точечной задачи проектирования имеем две пересекающиеся линии a1 и a2 с одинаковыми горизонтальными проложениями S, но разными наклонами. Пусть линии также заданы парой трехмерных координат. Тогда, для получения высоты точки 0 пересечения двух линий можно поступить следующим образом (рис. 7.35):
1)решая обратную задачу, определяем общее расстояние S между
концами линий и разность h1 и h2 высот краевых точек линии, а также уклон i, например, для линии 1-2;
2)используя теорему о подобии треугольников (см. рис. 7.35) можно записать, что
|
|
h1 |
= |
| h1 | +| h2 | |
→ S0 = |
h1 |
|
S , |
(7.30) |
|
|
|
S0 |
| h1 | + |
| h2 | |
||||||
|
|
|
S |
|
|
|
|
|||
откуда превышение h0 = i · S, а высота пересечения H0 = H1 + h0. |
|
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
1′ |
|
|
0 |
|
|
h2 |
|
|||
|
h1 |
|
S0 |
|
|
h0 |
|
2′ |
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
Н1 |
|
|
S |
Н0 |
|
|
|
|||
|
|
|
|
|
|
|||||
Рис. 7.35. Решение второй точечной задачи проектирования
Решение третьей точечной задачи в общем виде достаточно трудоемко, а сама она в таком виде встречается редко, но часто используется следующий частный случай: дан квадрат со стороной S и высотами в вершинах H1, H2 и H3. Очевидно, что три точки образуют плоскость. Требуется восстановить высоту H4 в четвертой вершине квадрата, но чтобы точка
принадлежала определенной выше плоско-
2 |
|
i2 |
|
|
|
3 |
сти (рис. 7.36). |
||
|
|
|
|
||||||
|
i1 |
|
H2 |
|
|
|
Задача достаточно просто решается, |
||
|
|
|
|||||||
|
|
|
|
|
|
H3 |
исходя из следующих рассуждений: так как у |
||
1 |
|
|
|
|
|
|
квадрата стороны взаимно параллельны, то |
||
|
|
|
|
|
|
|
уклоны у этих сторон в пространственном |
||
|
|
|
|
|
|
|
|||
H1 |
|
|
H4 |
|
4 S |
аналоге очевидно одинаковы и превышения |
|||
|
|
|
|||||||
|
|
|
между ними также одинаковы. Для рис 7.36 |
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
превышение по стороне 1-2 (Н2 – Н1) равно |
|
Рис. 7.36. Восстановление |
|||||||||
превышению между сторонами 4-3 (Н3 – Н4); |
|||||||||
|
4-й точки в квадрате |
превышение по стороне 2-3 (Н3 – Н2) равно |
|||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
346 |
|
превышению по стороне 1-4 (Н4 – Н1). Из сказанного следует, что превышения по сторонам 1-2 и 2-3 известны, так как известны высоты точек 1, 2 и 3 и высота точки 4 равна:
Н4 = Н1 + h1-4 = Н1 + (Н3 – Н2). |
(7.31) |
Линейные задачи проектирования в основном сводятся к проложе-
нию на топографическом плане линии заданного проектного уклона i. При этом уклон может быть интервальным в виде от i1 до i2. Достаточно часто возникает похожая задача нахождения на проектной плоскости линии уклона i.
Задача проложения линии заданного проектного уклона на топографическом плане с горизонталями решается следующим образом. По значению уклона i и высоте сечения рельефа h вычисляют величину заложения s (см. формулу (7.11))
s = h / i .
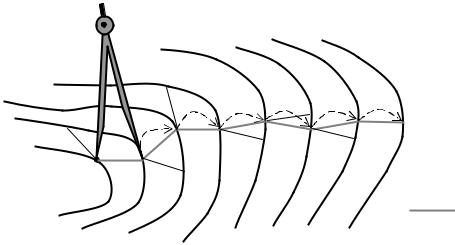
Если откладывать измерителем вычисленное расстояние от начальной горизонтали до следующей (рис. 7.37) с касанием, то в результате мы получим линию заданного уклона. На рисунке штрихами показаны симметричные альтернативные варианты в каждой точке.
s |
s |
s |
s |
s |
s |
|
|
|
|
|
s
s
Рис. 7.37. Отложение линии заданного уклона
Очевидно, что решение не однозначное. При этом, если величина рассчитанного заложения s меньше расстояния между горизонталями, то точки соединяют по кратчайшему расстоянию.
Если требуется на проектной плоскости, заданной тремя точками с начальной точкой 1 и уклонами по осям ix и iy получить направление α проектного уклона iпр, то поступают следующим образом. Предположим, что на плоскости точка 0 для проектного уклона iпр существует (рис. 7.38).
347
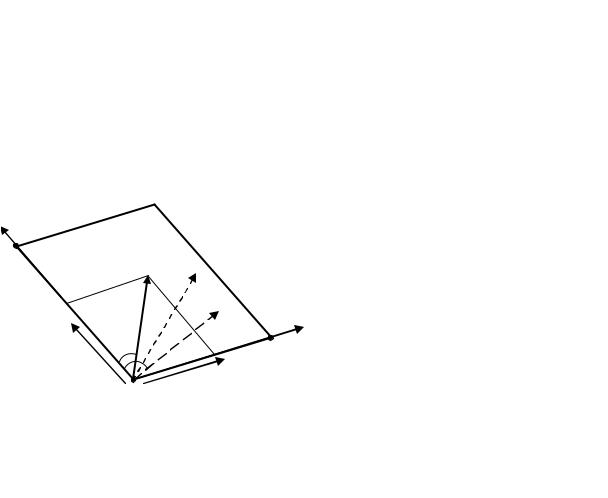
Тогда, чтобы определить её отметку Н0 относительно исходной точ- |
||||||
ки 1 с отметкой Н1 через известные уклоны, два раза совместно используем |
||||||
формулу (7.28) |
|
|
|
|
|
|
|
|
H0 = H1 +ix d1 +iy d2 . |
|
(7.32) |
||
Перенося Н1 в левую часть и относя обе части к общему расстоянию |
||||||
d, получим |
|
|
|
|
|
|
|
|
iпр. =ix cos(α) +iy sin(α) . |
|
(7.32а) |
||
|
|
|
Решая уравнение (7.32а) отно- |
|||
|
|
|
сительно α любым известным спо- |
|||
d2 |
H0 |
|
собом (например, сведением триго- |
|||
|
нометрических функций к тангенсу) |
|||||
0 |
imax. |
|||||
|
получим два решения (α1, α2) отно- |
|||||
iпр. |
||||||
d1 α |
d |
0′ |
сительно оси симметрии, характери- |
|||
α |
iпр. |
зующей максимальный уклон на по- |
||||
1 |
|
|||||
ix |
2 |
iy |
верхности imax. = iy / ix (см. рис. 7.37, |
|||
H1 |
||||||
|
альтернативные варианты). |
|
||||
Рис. 7.38. Определение направления |
|
|||||
При |
интервальном |
задании |
||||
проектного уклона на плоскости |
уклонов задача решается проще, |
|||||
|
|
|
||||
опять же на основе рассмотренной выше методики. |
|
|
||||
При проектировании плоскостей выделяют: |
|
|
||||
–проектирование горизонтальной плоскости на проектной высоте Н0
сбалансом и без баланса земляных работ;
–проектирование наклонной плоскости с балансом и без баланса земляных работ;
–проектирование планировки участка местности на топографическом плане набором пересекающихся плоскостей.
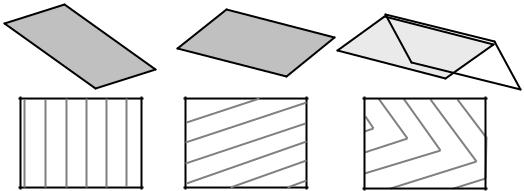
Для начала изложения уясним, что горизонтальная плоскость горизонталями не отображается. Отображение наклонных плоскостей и некоторых из часто встречающихся их комбинаций представлено на рис. 7.39.
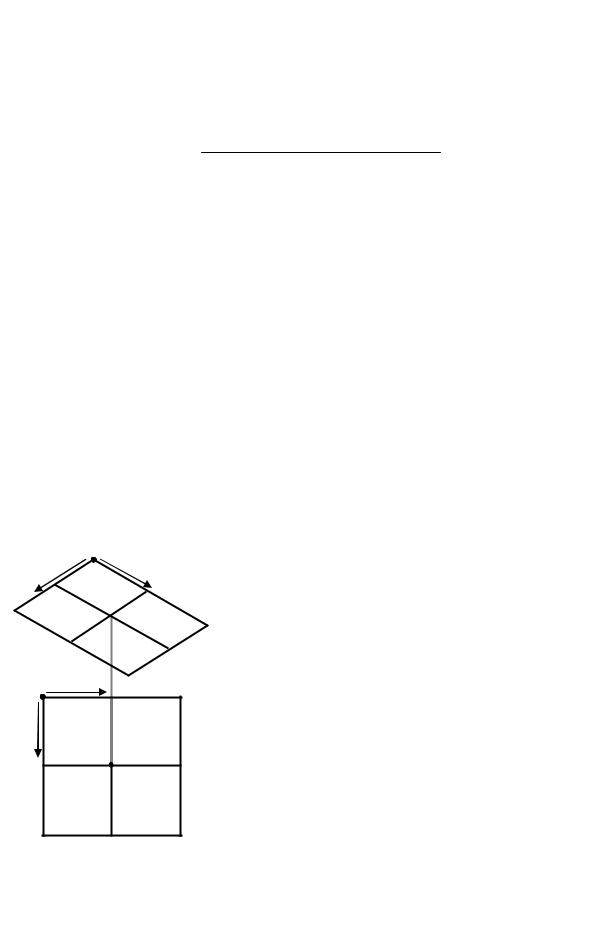
При проектировании на участке одной проектной горизонтальной плоскости при условии, что объем земли над плоскостью равен объему пустот под плоскостью (с балансом земляных работ) необходимо вычислить высоту проектной плоскости, по которой выполняется заявленное условие. Такая высота (иногда её называют среднее площадное) может быть проще всего получена при сеточном квадратном моделировании по-
верхности. Пусть (рис. 7.40) проектируемый участок разбит на квадраты со стороной S и имеет отметки вершин i и j сечений Hij.
348
Полученная высота Н0 и является искомой величиной, которую на- |
|||||||
зывают проектной отметкой при проектировании горизонтальной плоско- |
|||||||
сти с балансом земляных работ. Если сгруппировать отметки в вершинах в |
|||||||
формуле (7.33) по числу их использования, то получим другой, тоже часто |
|||||||
используемый, вид формулы для проектной отметки: |
|
||||||
|
|
H0 |
= 1 ∑H(1) + 2 ∑H(2) + 4 ∑H(4) , |
(7.33а) |
|||
|
|
|
|
4 n |
|
|
|
где Н(1), Н(2), Н(4) – отметки, принадлежащие 1, 2 и 4 квадратам соответ- |
|||||||
ственно, или участвующие в формуле (7.33) 1, 2 и 4 раза; |
|
||||||
n – число квадратов. |
|
|
|
|
|||
Очевидно, в самой общей формуле вида (7.33а) будет также сумма |
|||||||
отметок, принадлежащих 3 квадратам Н(3), в случае разрыва однородности, |
|||||||
то есть когда например, на рис 7.40 одна или несколько высот не участву- |
|||||||
ют по каким либо причинам в определении проектной отметки. |
|||||||
При проектировании наклонной плоскости с балансом земляных ра- |
|||||||
бот на участке как рис. 7.40 на первом этапе также необходимо получить |
|||||||
по (7.33) или (7.33а) проектную отметку, но не всей плоскости (напомина- |
|||||||
ем, она наклонная), а центра тяжести поверхности который определяется |
|||||||
точкой |
со |
средними |
координатами (Xср., Yср.) |
|
по осям |
из всех вершин |
|
(рис. 7.41). Таким образом, проектируемая плоскость на первом этапе фик- |
|||||||
сируется своим центром тяжести на высоте проектной отметки Н0. Оче- |
|||||||
|
|
0 |
|
видно, что в каком либо виде должны быть |
|||
ix |
|
заданы величины, характеризующие на- |
|||||
iy |
|
||||||
|
|
|
|
клон плоскости относительно горизонталь- |
|||
|
|
|
|
ной по оси X и Y. Чаще всего это состав- |
|||
|
|
|
|
ляющая задается в виде уклонов по осям, |
|||
|
1 |
2 |
|
совмещенным |
с |
краями |
проектируемой |
|
iy |
|
плоскости, условными ix |
и/или iy, относи- |
|||
0 |
|
|
|||||
|
|
|
тельно вершины, выбранной за исходную |
||||
|
|
|
|
||||
ix |
|
Ц |
s |
(рис. 7.41, точка 0). |
|
||
|
|
2 |
Учитывая, что у параллельных линий |
||||
|
|
|
на плоскости уклоны одинаковы и зная дли- |
||||
|
|
|
|
ну стороны квадрата s и отметку центра тя- |
|||
|
|
|
|
жести Ц, не сложно вычислить на основе |
|||
Рис. 7.41. Схема проектирования |
решения задачи определения высоты по |
||||||
наклонной площадки |
проектной линии на расстоянии s (форму- |
||||||
с балансом земляных работ |
лы (7.28) или (7.29)) отметки точек 1, 2 и т.д. |
||||||
|
|
|
|
350 |
|
|
|
