1. Задача лінійного програмування та методи її розв’язування

1.1. Загальна економіко-математична модель задачі лінійного програмування. Приклади побудови лінійних економіко-математичних моделей

Умовно задачі математичного програмування, які полягають в дослідженні функції на екстремум, на змінні якої накладені певні обмеження, можна розділити на задачі:

• детермінованого і стохастичного програмування (залежно від імовірнісного характеру початкових параметрів моделі);

• динамічного і статичного програмування (залежно від обліку чинника часу);

• лінійного і нелінійного програмування (залежно від виду цільової функції і обмежень).

Задачі, в яких критерій оптимальності не є випадковою функцією параметрів, а параметри також не є випадковими величинами, називаються детермінованими. Наприклад, якщо в економіко-математичній моделі величини задані своїми математичними очікуваннями, то така задача є детермінованою.

Задачі, в яких критерій оптимальності є випадковою функцією параметрів, тобто включають невизначеність, називаються стохастичними. Задачі, в яких знаходження оптимального рішення можна розглядувати як миттєвий акт, називаються статичними.

Задачі, в яких знаходження оптимального рішення економіко-математичної моделі можна розглядувати не як застигле завдання, а в динаміці, знаходячи вирішення на декілька періодів часу, називаються динамічними. У динамічному програмуванні розглядуються методи, що дозволяють шляхом багатокрокової оптимізації отримати спільний оптимум. Наприклад, якщо суб’єкт в ході ухвалення рішення змінює свій інформаційний стан, отримуючи або втрачаючи інформацію, то в цьому випадку рішення доцільно приймати поетапно (багатокрокове рішення). Наприклад якщо розглядується план розвитку підприємства до 2010 року, мають бути обґрунтовані значення відповідних мікроекономічних показників не лише на 2010 рік, а і на всі проміжні роки, тобто врахована динаміка розвитку господарської діяльності даного підприємства.

Задачі, в яких критерій оптимальності (цільова функція) і система обмежень є лінійними, називаються задачами лінійного програмування (ЗЛП). Інакше виникає задача нелінійного програмування. Важливою перевагою задач лінійного програмування є те, що для їх розв’язування розроблений універсальний метод – симплекс-метод. Для деяких класів ЗЛП розроблені більш ефективні методи розв’язування. Наприклад, розподільчі задачі можна розв’язувати симплекс-методом, проте ефективнішим для їх розв’язування є метод потенціалів.

Лінійні моделі частенько є неадекватними природі об'єкту або процесу, що моделюються, тому доводиться будувати нелінійні моделі. Вирішувати нелінійні задачі складніше, ніж лінійні, оскільки немає універсальних методів розв’язування таких задач. Для деяких видів нелінійних задач розроблені чисельні спеціальні ефективні методи розв’язування, такі як метод найскорішого спуску, метод дроблення кроку. Проте, на практиці частіше використовують лінійні економіко-математичні моделі. Часто нелінійні залежності апроксимують лінійними. Моделі лінійного програмування знаходять широке вживання при розв’язуванні планових задач в різних сферах господарської діяльності.

Задачі, в яких критерій оптимальності є сумою функцій, кожна з яких залежить лише від однієї змінної, називаються задачами сепарабельного програмування.

Задачі, в яких на змінні накладена умова цілочисельності, називаються задачами цілочисельного програмування. Багато економічних задач характеризуються тим, що обсяги ресурсів можуть набувати лише цілих значень, такі як автомобілі, побутова техніка і інші об'єкти.

Задачі, в яких критерій оптимальності є опуклою функцією, називаються задачами опуклого програмування. Для таких задач існує ряд ефективних і обґрунтованих методів їх розв’язування. ЗЛП є окремим випадком завдань опуклого програмування.

Задачі, в яких критерій оптимальності є квадратичною функцією і система обмежень лінійна, називаються задачами квадратичного програмування.

Розглядують так само окремі класи завдання дробово-лінійного програмування, коли система обмежень є лінійною, а цільова функція – дробово-лінійна; задачі параметричного програмування, коли система обмежень є лінійною, а цільова функція містить параметр.

Особливий клас представляють задачі теорії ігор, які широко застосовуються в ринковій економіці. Серед них найбільш вивчені матричні парні ігри.

Процес побудови математичної моделі починається з відповідей на наступні питання:

1) Для визначення яких величин має бути побудована модель, тобто як ідентифікувати змінні задачі?

2) Які обмеження мають бути накладені на змінні, щоб виконувалися умови, які характерні для модельованої системи?

3) У чому полягає мета завдання, для досягнення якої зі всіх допустимих значень змінних потрібно вибрати ті, які відповідатимуть оптимальному рішенню задачі?

Розгледимо деякі загальні моделі і завдання.

Задача виробничого планування.

Деякий економічний суб'єкт (підприємство, цех, фірма) може виробляти п видів деякої продукції. В процесі виробництва використовується т видів ресурсів (сировини). Вживані технології характеризуються нормами витрат сировини на одиницю продукту, що виробляється, – a_ij – норма витрати сировини i-го виду виробництво одиниці продукції j-го виду. Відомі обмеження на ресурси, які витрачаються в процесі виробництва – b_i – запас сировини i-го виду а також дохід від одиниці продукції j-го виду – с_j. Визначити план виробництва, який надасть найбільший сумарний дохід суб'єкту господарювання.

Для побудови економіко-математичної моделі умову задачі зручно представити в таблиці 1.1.1

Таблиця 1.1.1

Умова задачі виробничого планування

Вид сировини	Норма витрат сировини i-го виду на виробництво одиниці продукції j-го виду				Запас сировини
	Вид продукції
	1	2	…	П
1	а11	а12	…	а1п	b1
2	а21	а22	…	а2п	b2
…	…	…	…	…	…
Т	ат1	ат2	…	атn	bт
Доход від одиниці продукції	с1	с2	…	сп

Позначимо через х_j – кількість продукції j-го виду.

В рамках описаних вище технологій на виробництво всієї продукції першого виду витрати сировини першого виду складають а₁₁х₁, на виробництво всієї продукції другого виду – а₁₂х₂, і, так далі, на виробництво всієї продукції п-го виду – а_1пх_п. Загальні витрати сировини першого виду можна представити як суму:

а₁₁х₁ + а₁₂х₂ + … + а_1пх_п.

Оскільки запаси сировини обмежені, то ця сума не може перевищувати величину запасу сировини першого виду – b₁, тобто

а₁₁х₁ + а₁₂х₂ + … + а_1пх_п b₁.

Проводячи аналогічні міркування для всіх видів сировини, отримаємо останні нерівності системи обмежень:

а₂₁х₁ + а₂₂х₂ + … + а_2пх_п b₂,

……………………………….

а_т1х₁ + а_т2х₂ + … + а_тпх_п b_т.

До наведеної системи обмежень також слід додати природні обмеження на невід’ємність змінних х₁, х₂, … , х_п, оскільки кількість продукції любого виду не може бути від’ємною величиною.

Доход, що отримано від виробництва всієї продукції першого виду, дорівнює с₁х₁, від виробництва всієї продукції другого виду – с₂х₂, і так далі, від виробництва всієї продукції п-го виду – с_пх_п . Сумарний доход дорівнює

с₁х₁ + с₂х₂ + … + с_пх_п.

Таким чином, задача виробничого планування полягає в находженні таких змінних х₁, х₂, …, х_п, які задовольняють системі обмежень

и надають функції доходу z = с₁х₁ + с₂х₂ + … + с_пх_п максимум.

Задача оптимальної загрузки обладнання.

Підприємству потрібно випустити продукції П₁ по плану N₁ одиниць, продукції П₂ – N₂ одиниць, і так далі, продукції П_k – N_k одиниць. Продукція обробляється на взаємозамінюємому обладнанні В₁, В₂, …, В_т різної потужності. Також відомі величини: a_ij – норма часу на обробку одиниці продукції i-го виду на обладнанні j-го виду; А_j – фонд часу обладнання j-го виду, с_ij – собівартість обробки продукції i-го виду на обладнанні j-го виду. Слід спланувати випуск продукції П_j таким чином, щоб собівартість її була найменшою и план випуску продукції було виконано.

Для побудови економіко-математичної моделі умову задачі доцільно представити в таблиці 1.1.2.

Таблиця 1.1.2

Умова задачі оптимальної загрузки обладнання

Вид обладнання	Собівартість обробки продукції i-го виду на обладнанні j-го виду				Фонд часу обладнання
	Вид продукції
	П1	П2	…	Пk
В1	а11	а12	…	а1k	А1
В2	а21	а22	…	а2k	А2
…	…	…	…	…	…
Вт	ат1	ат2	…	атk	Ат
План випуску продукції	N1	N2	…	Nk

Позначимо х_ij – кількість продукції i-го виду, яка обробляється на обладнанні j-го виду.

Фактичні витрати часу на обробку всієї продукції П₁ на обладнанні В₁ складають а₁₁х₁₁, на обробку всієї продукції П₂ на обладнанні В₁ – а₁₂х₁₂, і, так далі, на обробку всієї продукції П_k – а_1пх_1п. Загальні витрати часу на обробку всієї продукції на обладнанні В₁ можна представити як суму:

а₁₁х₁₁ + а₁₂х₁₂ + … + а_1kх_1k.

Оскільки фактичні витрати часу не можуть перевищувати відведені фонди, то ця сума не може перевищувати А₁, тобто маємо нерівність

а₁₁х₁₁ + а₁₂х₁₂ + … + а_1kх_1k А₁.

Проводячи аналогічні міркування для всіх видів обладнання, отримаємо інші нерівності системи обмежень:

а₂₁х₂₁ + а₂₂х₂₂ + … + а_2kх_2k А₂,

……………………………….

а_т1х_т1 + а_т2х_т2 + … + а_тkх_тk А_т.

Оскільки за умовами задачі план необхідно виконати, то маємо систему обмежень:

х₁₁ + х₂₁ + … + х_m1 = N₁.

х₁₂ + х₂₂ + … + х_m2 = N₂,

…………………………

х_1т + х_2т + … + х_тk = N_k.

До системи обмежень також слід додати природні обмеження на невід’ємність змінних х₁, х₂, … , х_п, оскільки кількість продукції любого виду не може бути від’ємною величиною.

Загальна собівартість продукції, що обробляється, дорівнює

z=c₁₁х₁₁+c₁₂х₁₂+…+c_1kх_1k+c₂₁х₂₁+c₂₂х₂₂+…+c_2kх_2k+…+c_т1х_т1+c_т2х_т2+…+c_тkх_тk.

Таким чином, задача полягає в находженні таких змінних х₁, х₂, …, х_п , які задовольняють системі обмежень

и надають функції собівартості мінімум.

Задача про суміші.

До таких задач відноситься клас математичних моделей, що стосується економічних проблем, які пов’язані з виготовленням різних сумішей (сплавів металів, хімічних речовин, виробництва нафтопродуктів тощо).

Фірма має можливість купувати т різних видів сировини і готувати різні види сумішей. Кожен вид сировини містить різну кількість живильних компонентів (інгредієнтів). Продукція повинна задовольняти хоч би мінімальним вимогам з точки зору корисності (поживності). Перед керівництвом фірми стоїть задача визначити кількість кожного виду сировини, що створює суміш мінімальної вартості при дотриманні вимог до спільної витрати суміші і її поживності.

Нехай х_i – кількість i-го виду сировини в суміші; т – кількість видів сировини; п – кількість інгредієнтів в суміші; а_ij – кількість інгредієнту j-го виду, що знаходиться в одиниці i-го виду сировини; b_j – мінімальна кількість інгредієнту j-го виду, що знаходиться в одиниці суміші; с_i – вартість одиниці сировини i-го виду; q – мінімальна загальна вага суміші, що використовується фірмою.

Для побудови економіко-математичної моделі умову задачі зручно представити в таблиці 1.1.3.

Таблиця 1.1.3

Умова задачі про суміші

Вид Інгредієнту	Кількість інгредієнту j-го виду, що знаходиться в одиниці i-го виду сировини				мінімальна кількість інгредієнту
	Види сировини
	1	2	…	П
1	а11	а12	…	а1п	b1
2	а21	а22	…	а2п	b2
…	…	…	…	…	…
Т	ат1	ат2	…	атn	bт
Собівартість одиниці сировини	с1	с2	…	сп

В одиниці сировини першого виду міститься а₁₁ одиниць першого інгредієнту, а у всій кількості сировини першого виду цього інгредієнту міститься а₁₁х₁. Цього ж інгредієнту в одиниці сировини другого виду міститься а₁₂ одиниць, а всій кількості сировини другого виду цього інгредієнту міститься а₁₂х₂ і так далі, а_1nх_n – кількість першого інгредієнту в п-му виді сировини. Загальна кількість сировини першого виду, що міститься у всіх сумішах, дорівнює

а₁₁х₁ + а₁₂х₂ + … + а_1nх_n.

Оскільки відомо, що мінімальна кількість інгредієнта першого виду, що міститься в одиниці суміші дорівнює b₁, то маємо обмеження

а₁₁х₁ + а₁₂х₂ + … + а_1nх_nb₁ .

Розгледимо другий вид інгредієнту. Необхідно врахувати вміст цього інгредієнту у всій кількості суміші сировини першого виду, другого і так далі до п-го виду сировини. Підсумовуючи окремі значення кількості одиниць другого виду інгредієнту у всіх сумішах, отримаємо загальну кількість другого виду інгредієнту. Вона має бути не менше мінімальної кількості інгредієнту другого виду, що міститься в одиниці суміші b₂. Аналогічно попереднім міркуванням, можна встановити співвідношення між вмістом інгредієнту будь-якого виду у всіх сумішах і мінімальною кількістю цього інгредієнту в суміші. В результаті прийдемо до системи обмежень на поживність суміші:

а11х1 + а12х2 + … + а1nхn b1. а21х1 + а22х2 + … + а2nхn b2, ………………………………. ат1х1 + ат2х2 + … + атnхn bт.

Змінні х₁, х₂, …, х_n , що представляють собою кількості інгредієнта першого, другого і т.д., до п-го виду, не можуть бути від’ємними. У випадку, якщо який-небудь інгредієнт не входить в склад суміші, то відповідна змінна буде дорівнювати нулю. Таким чином, прийдемо до системи обмежень на невід’ємність змінних

х₁ 0,х₂0, …,х_n 0.

У зв’язку з тим, що відомо мінімальну загальну вагу суміші q, що використовується фірмою, прийдемо до обмеження на витрату суміші

х₁ + х₂ + … + х_n q.

Оскільки ціна одиниці сировини першого виду дорівнює с₁, можемо обчислити вартість всієї сировини першого виду – с₁х₁. Аналогічно вартість всієї сировини другого виду – с₂х₂ и т.д., вартість всієї сировини п-го виду – с_nх_n. Сумарна вартість всіх видів сировини, що використовуються в приготуванні суміші, дорівнює сумі всіх цих вартостей.

Таким чином, задача про суміші полягає в находжені величин х₁, х₂, …, х_n , що задовольняють обмеженням

а11х1 + а12х2 + … + а1nхn b1. а21х1 + а22х2 + … + а2nхn b2, ………………………………. ат1х1 + ат2х2 + … + атnхn bт. х1 + х2 + … + хn q. х1 0,х20, …,хn 0

и надають мінімум цільовій функції

z = с₁х₁ + с₂х₂ +…+ с_nх_n.

Транспортна задача.

Однією із задач господарського управління, що часто зустрічаються, є задача щодо розробки раціонального плану транспортних перевезень. Основна мета організації перевезень – мінімізація витрат на їх здійснення. Таке задачі носять назву транспортних.

Транспортна задача належить до спеціального класу розподільчих задач лінійного програмування. Хай потрібно перевезти однорідний вантаж з m пунктів постачання А₁, А₂,…,А_т в n пунктів споживання B₁, B₂,…, B_п. Відома кількість вантажу a_i (запаси), що знаходиться у i-го постачальника (постійно), а також обсяги потреб в ньому b_j (заявки) j-го споживача. Відома величина витрат на перевезення одиниці вантажу від i-го постачальника до j-го споживача – тариф – с_ij. Необхідно розподілити вантаж таким чином, щоб витрати на його перевезення були мінімальними.

Позначимо х_ij – кількість вантажу, що перевозиться з i-го пункту постачання в j-й пункт споживання.

Рішення (план перевезень) визначається матрицею розміру ()

.

Загальна кількість вантажу, що є у кожного постачальника не може перевищувати його запасів:

х₁₁ + х₁₂ + … + х_1п а₁.

х₂₁ + х₂₂ + …+ х_2п а₂,

……………………….

х_т1 + х_т2 + … + х_тп а_т.

Заявки, які подані пунктами споживання, повинні бути виконані:

х₁₁ + х₂₁ + … + х_m1 = b₁.

х₁₂ + х₂₂ + … + х_m2 = b₂,

…………………………

х_1т + х_2т + … + х_тп = b_п.

Природно, що все невідомі не можуть приймати від’ємні значення, тобто .

Загальна вартість перевезень дорівнює

z=c₁₁х₁₁+c₁₂х₁₂+…+c_1пх_1п+c₂₁х₂₁+c₂₂х₂₂+…+c_2пх_2п+…+c_т1х_т1+c_т2х_т2+…+c_тпх_тп

Таким чином, задача полягає в находженні таких змінних , які задовольняють системі обмежень

и надають функції транспортних витрат мінімум.

Узагальнюючи приклади, що розглянули, можна зробити наступні висновки:

• обмеження в задачах лінійного програмування можуть бути виражені як рівностями, так і нерівностями.

• лінійна функція може прагнути як до максимуму, так і до мінімуму.

• змінні в задачах завжди невід’ємні.

В економіці задачі умовної оптимізації виникають при реалізації принципу оптимальності в плануванні і управлінні, суть якого полягає в прагненні вибрати таке планово-управлінське рішення яке щонайкраще враховувало б внутрішні можливості і зовнішні умови виробничої діяльності суб'єкта господарювання.

Реалізувати на практиці принцип оптимальності в плануванні і управлінні – це означає розв’язати екстремальну задачу:

,, або,, (1.1.1)

де – цільова функція – математичних запис критерію оптимальності.

В задаче лінійного програмування (ЗЛП) потрібно знайти екстремум (максимум або мінімум) цільової функції :

, (1.1.2)

при обмеженнях:

(1.1.3)

В формулах (1.1.2), (1.1.3) – задані постійні величини, причому; символозначає, що в конкретній ЗЛП можливо обмеження типа рівності або нерівності.

ЗЛП (1.1.2), (1.1.3) можна записати в наступних формах: канонічній, векторній, матричній.

Канонічна форма ЗЛП має вид (1.1.4), (1.1.5):

, (1.1.4)

, (1.1.5)

.

Векторна форма ЗЛП має вид (1.1.6), (1.1.7):

, (1.1.6)

, (1.1.7)

,

де .

Матрична форма ЗЛП має вид (1.1.8), (1.1.9):

, (1.1.8)

,, (1.1.9)

де - матриця розмірності,,.

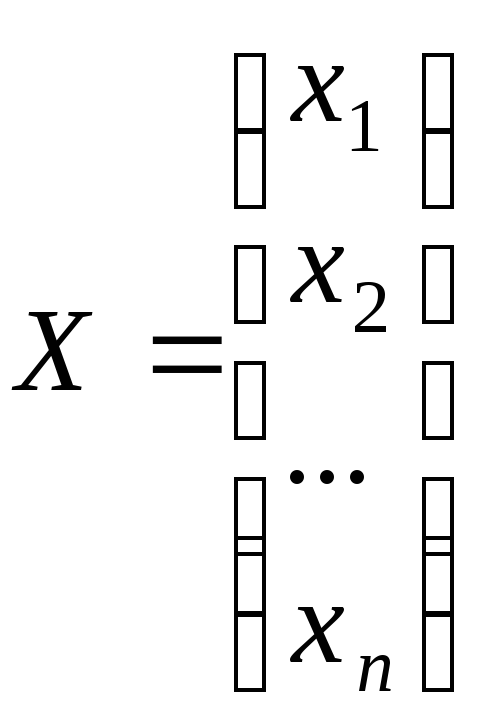Планом ЗЛП або допустимим розв’язком ЗЛП називається вектор , який задовольняє системі обмежень (1.1.3).

Оптимальним планом ЗЛП або оптимальним допустимим розв’язком ЗЛП називається план ЗЛП, який оптимізує цільову функцію (1.1.2).

Багатокутником розв’язків ЗЛП або областю допустимих розв’язків ЗЛП називається сукупність точок, що задовольняє системі нерівностей (1.1.3).

Для розв’язування ЗЛП наведемо наступні твердження.

Теорема 1. Область допустимих розв’язків задачі лінійного програмування є опуклою множеною.

Множина називається опуклою, якщо разом з двома крапками йому належить і відрізок їх сполучає. Точка множини називається граничною, якщо в будь-якому її околі містяться як точки, які належать множині, так і точки, які їй не належать. Сукупність граничних точок множини утворює її границю. Границя опуклого багатокутника на плоскості складається з відрізків або прямих. Точки, в яких перетинаються відрізки або прямі границі багатокутника, називаються вершинами. Перетином областей називається множина точок, які належать кожній з цих областей.