FIZIKA_kospekt_lektsy

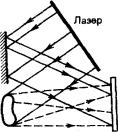
27.6. Понятие о голографии

Голография — особый способ записи и последующего восстановления

волнового поля, основанный на регистрации интерференционной картины. Она обязана своим возникновением законам волновой оптики — законам интерференции и дифракции.

Это принципиально новый способ фиксирования и воспроизведения пространственного изображения предметов стали возможными после

появления источников света высокой степени когерентности — лазеров.

Рассмотрим элементарные основы принципа голографии, т. е.

регистрации и восстановления информации о предмете рис. 27.7. Для

информации кроме волны, идущей от предмета (так называемой предметная волна), используют еще когерентную с ней волну, идущую от источника света

(так называемую опорную волну).

Идея голографирования состоит в том, что фотографируется распределение интенсивности в интерференционной картине, возникающей при суперпозиции волнового поля объекта и когерентной ему опорной волны известной фазы. Последующая дифракция света на зарегистрированном распределении почернений в фотослое восстанавливает волновое поле объекта и допускает изучение этого поля при отсутствии объекта.

Практически эта идея может быть осуществлена с помощью принципиальной схемы, показанной на рис 27.7. Лазерный пучок делится на две части, причем одна его часть отражается зеркалом на фотопластинку

(опорная волна), а вторая попадает на фотопластинку, отразившись от предмета

(предметная волна). Опорная и предметная волны, являясь когерентными и накладываясь, друг на друга, образуют на фотопластинке интерференционную картину. После проявления фотопластинки и получается голограмма — зарегистрированная на фотопластинке интерференционная картина,

образованная при сложении опорной и предметной волн.

281

Для восстановления изображения голограмма помещается в то же самое положение, где она находилась до регистрации. Ее освещают опорным пучком того же лазера (вторая часть лазерного пучка перекрывается диафрагмой). В

результате дифракции света на интерференционной структуре голограммы восстанавливается копия предметной волны, образующая объемное (со всеми присущими предмету свойствами) мнимое изображение предмета,

расположенное в том месте, где предмет находился при голографировании. Оно кажется настолько реальным, что его хочется потрогать. Кроме того,

восстанавливается еще действительное изображение предмета, имеющее рельеф, обратный рельефу предмета, т. е. выпуклые места заменены вогнутыми,

и на оборот.

Обычно пользуются мнимым голографическим изображением, которое по зрительному восприятию создает полную иллюзию существования реального предмета. Рассматривая из разных положений объемное изображение предмета,

даваемое голограммой, можно увидеть более удаленные предметы, закрытые более близкими из них.

Голограмму можно расколоть на несколько кусков. Но даже малая часть голограммы восстанавливает полное изображение. Однако уменьшение размеров голограммы приводит к ухудшению четкости получаемого изображения. Это объясняется тем, что голограмма для опорного пучка служит дифракционной решеткой, а при уменьшении числа штрихов дифракционной решетки (при уменьшении размеров голограммы) ее разрешающая способность уменьшается.

Применение голограммы разнообразны, но наиболее важными, являются запись и хранение информации. В качестве будущих разработок могут служить ЭВМ с голографической памятью, голографическое изображение будущих строительных объектов, голографический электронный микроскоп,

голографическое кино и телевидение и т.д. Значительный интерес представляет акустическая голография. Когерентные звуковые волны получить легко, а звук

(или ультразвук) хорошо распространяется в жидкостях или твердых телах.

Поэтому легко получить трехмерную акустическую голограмму непрозрачных предметов. Восстановив, затем изображение в видимом свете, получают возможность увидеть внутреннее строение тел, например, структуру металлического стержня, бетонной балки.

282

ГЛАВА 28. РЕНТГЕНОВСКИЙ АНАЛИЗ

28.1. Рентгеновские лучи

Рентгеновские лучи представляют собой электромагнитное излучение с длиной волны λ от 10-12 до 10-8 м. В рентгеноструктурном анализе используются лучи с длинами волн, заключенными в интервале (0,5-0,2) 10-10 м. Лучи с λ<2 10-10м условно называются жесткими, а с λ>2 10-10м - мягкими. У

рентгеновских лучей от длины волны зависит их проникающая способность,

чем меньше длина волны, тем легче они проходят через вещество. Они невидимы, слегка преломляются, проходят через непрозрачные для видимого света тела, производят фотографическое действие, ионизируют газы, вызывают люминесценцию многих веществ, оказывает воздействие на биологические объекты.

Кристаллы, являясь трехмерными пространственными решетками, имеют постоянную решетки порядка 10-10м и, следовательно, непригодны для наблюдения дифракции в видимом свете (5 10-7 м). Эти факты позволили М.Лауэ прийти к выводу, что в качестве естественных дифракционных решеток для рентгеновского излучения можно использовать кристаллы, поскольку расстояние между атомами в кристаллах одного порядка с λ рентгеновского излучения (10-12÷10-8 м).

Простой метод расчета дифракции рентгеновского излучения от кристаллической решетки предложен Г. В. Вульфом и Г. и Л. Брэггами. Они предположили, что дифракция рентгеновского излучения является результатом

скольжения θ (угол между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн 1' и 2",

283

интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решетки. Максимумы интенсивности (дифракционные мак-

симумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться, в одинаковой фазе. Эти направления удовлетворяют формуле Вульфа—Брэггов

d sin θ = т λ (m= 1,2,3,…,), (28.1)

т. е. при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому длин волн λ наблюдается дифракционный максимум.

28.2. Источники рентгеновских лучей

Рентгеновские лучи получают с помощью рентгеновских трубок, которая содержит катод, фокусирующий колпачок, бериллиевые окна для выпуска рентгеновских лучей, защитный цилиндр, анод, стеклянная колба. Трубка откачивается до высокого вакуума (10-5Па). Для охлаждения анода трубки применяется проточная вода или масло. Катод трубки изготавливают из вольфрамовой спирали, помещенный в фокусирующий колпачок, приводящий к сужению пучка электрона. Анод представляет собой полый цилиндр,

изготавливаемый из материала с высокой теплопроводностью, чаще всего из меди. Мощность трубок колеблется от 0,01 до 50 кВт. Рентгеновский аппарат содержит высоковольтный трансформатор с напряжением 0-99кВ,

трансформаторы накала трубки, пульт управления (на котором размешают автотрансформатор, выключатель высокого напряжения, вольтметр и миллиамперметр).

Рентгеновские трубки имеют вольтамперную характеристику (ВАХ).

Меняя ток накала трубки, можно изменять ее ВАХ, а, следовательно, и

величину анодного тока. Поэтому анодный ток стабилизируют. Рентгеновская трубка работает на участке насыщения ВАХ, причем ток насыщения тем выше,

чем выше ток накала трубки. Для структурного анализа необходимо, чтобы трубка давала нужную длину волны излучения, обладая высокой удельной мощностью излучения.

Принцип работы рентгеновской трубки таков. При определенном токе накала в результате термоэлектронной эмиссии электроны вылетают из катода

284

и под действием высокого напряжения U с большой скоростью направляются на зеркало антикатода и тормозятся им. При этом около 99% их кинетической энергии переходит в тепло (вот почему анод охлаждается) и лишь 1% их энергии преобразуется в рентгеновское излучение, состоящее из непрерывного

(сплошного) излучения (спектра) и наложенного на него линейчатого

(характеристического) излучения (спектра).

Сплошное излучение возникает в результате многократных взаимодействий атомов мишени (анода) с пучком электронов; оно называется также тормозным, т.к. возникает в результате торможения электронов веществом анода, точнее в результате их рассеяния в электрическом поле атомных ядер и электронов. Сплошное излучение простирается от максимальной частоты νmax когда вся энергия электрона преобразуется в рентгеновское излучение в область более низких частот.

С повышением напряжения на трубке наступает такой момент, когда наряду с увеличением интенсивности сплошного спектра и смещения в сторону коротких волн на фоне этого спектра при определенном для данного анода минимальном ускоряющем напряжении U0 (потенциале возбуждения)

возникает (характеристическое) линейчатое излучение.

Характеристическое излучение возникает в том случае, когда энергия падающего электрона оказывается достаточной для выбивания из атома мишени внутреннего электрона. Тогда на освободившееся место перейдет один из внешних электронов атома и произойдет испускание кванта рентгеновских лучей. Интенсивность характеристического излучения примерно в 100 раз выше, чем сплошного.

Характеристическое излучение – чисто квантовый процесс - оно возникает при электронных переходах в атомах с одного энергетического уровня на другой. Сплошной спектр возникает в результате изменения кинетической энергии пучка.

Характеристический спектр рентгеновских лучей состоит из нескольких серий линий, отличающихся друг от друга по интенсивности и длинам волн.

Для тяжелых элементов найдено 5 таких серий линий, которые обозначаются

K,L,M,N,O. Чем выше атомный номер элемента в периодической системе, тем жестче характеристические лучи и тем выше потенциал их возбуждения (для

285

выбивания электрона из атома вещества анода). Наибольшее значение в рентгеноструктурном анализе имеет К-серия; она содержит только 3 линии заметной интенсивности. При повышении напряжения интенсивность линии К-

серии растет по закону степенной функции

где k2 – коэффициент пропорциональности = 0,8 10-4.

Линии К-серии состоят из α и β составляющих, причем Кα в свою очередь

состоит из Кα1 и Кα2.

Относительную интегральную интенсивность линий определяют при определении структуры вещества, искажений кристаллической решетки,

характеристической температуры, изучении сверхструктуры и др. Интегральная интенсивность линий рентгенограммы является функцией ряда факторов. Эта

зависимость выражается уравнением:

где I0 –интенсивность первичных лучей;

С - постоянная величина для данного вещества и данных условий съемки;

р – множитель повторяемости – равен числу семейств плоскостей в их совокупности, имеющих одинаковое межплоскостное расстояние и одинаковый структурный множитель;

f(θ) – угловой множитель интенсивности – учитывает поляризацию,

происходящую при рассеянии рентгеновских лучей, а также конечную величину пучка рассеянных лучей и геометрию съемки;

|S|2 – структурный множитель интенсивности – учитывает зависимость интенсивности рентгеновских лучей от расположения атомов в элементарной ячейке и определяется базисом решетки;

e –2М – температурный множитель интенсивности – учитывает разность фаз рассеянный лучей, возникающую вследствие тепловых колебаний;

1 - объем элементарной ячейки;

Vя

f2 – атомный множитель – учитывает расположение электронов,

рассеивающих лучи, в объеме атома и является функцией sinθ/λ;

286

А(θ) – абсорбционный множитель – учитывает ослабление лучей в образце при данной геометрии съемки.

28.3. Основные методы рентгеноструктурного анализа

Использование рентгеновского анализа для изучения строительных материалов, металлов и сплавов.

Среди методов, изучающих структуру различных материалов, одно из ведущих мест занимает рентгеноструктурный анализ - совокупность методов исследования атомной структуры вещества по дифракционной картине по дифракционной картине, полученной при взаимодействии его с

рентгеновскими лучами.

Установление вещества по данным о межплоскостных расстояниях.

Каждая фаза исследуемого вещества имеет свою кристаллическую решетку.

Семейства атомных плоскостей, образующих эту решетку, обладают своим,

характерным только для данной решетки набором значений межплоскостных расстояний d(hkl). Данные о межплоскостных расстояниях для различных фаз

можно найти в специальных таблицах, справочной литературе. Значения d(hkl)/n

(n-целые числа (1,2,3...), или так называемый порядок отражения) можно

λ/2sin θ(hkl). Поскольку λ (длина волны характеристического излучения, в

котором получена рентгенограмма) величина известная, то задача определения межплоскостных расстояний d/n сводится к нахождению углов θ для всех линий рентгенограммы.

Качественный фазовый рентгеноструктурный анализ. Рентгенограмма многофазной системы представляет собой результат наложения рентгенограмм отдельных фаз, интенсивности которых пропорциональны количеству фазы в системе. Поэтому фаза, содержание которой в системе невелико, будет

287

представлена на рентгенограмме лишь небольшим числом наиболее интенсивных линий.

Необходимо определить межплоскостные расстояния по формуле Вульфа-Брэгга. Для установления природы фаз, присутствующих в системе,

следует из общего ряда полученных значений dНКL выделить ряды,

свойственные каждой из фаз в отдельности. Затем сопоставить их с табличными значениями для каждой из фаз и, проиндицировав соответствующие интерференционные максимумы, рассчитать значения периодов решеток соответствующих фаз.

Если о природе фазы нельзя сделать достаточно надежных предположений, то сначала следует выяснить сингонию фазы, затем определить ее периоды и дифракционную группу и по периодам установить природу фазы,

пользуясь таблицами (кубическая сингония) номограммами (графическое индицирование вещества по номограммам Бьернстрема, Липсона, Ито) для тетрагональной гексагональной, моноклинной и триклинной сингонии.

Количественный фазовый рентгеноструктурный анализ. Рентгеновский количественный фазовый анализ поликристаллических веществ основан на том,

что интегральная интенсивность дифракционных линий, принадлежащих разным фазам, зависит от концентрации этих фаз в веществе (сплаве). С другой стороны, при одном и том же содержании определяемой фазы интенсивность ее линий зависит от отражательной способности соответствующего семейства кристаллографических плоскостей и от соотношения коэффициентов ослабления рентгеновских лучей для исследуемой фазы и всего сплава

(вещества).

На сопоставлении интенсивностей линий определяемых фаз, выбранных в качестве линий сравнения, основаны различные способы количественного фазового анализа без применения и с применением эталонов.

Метод гомологических пар. Применяется для анализа двухфазных систем при условии, что μ1 = μ2. Известно, что каждая фаза дает на рентгенограмме линии разной интенсивности. Если рентгенографируется двухфазная смесь, то интенсивность линий каждой из фаз тем больше, чем больше количество

288

данной фазы в смеси. Интенсивность двух линий, принадлежащих разным фазам, могут быть одинаковы лишь при определенном количественном соотношении каждой из фаз в смеси. Такие пары называются гомологическими парами. Если заранее составить таблицу таких пар по эталонным смесям или использовать уже готовую из справочной литературы, то, находя на рентгенограмме две близлежащие дифракционные линии от разных фаз с одинаковой интенсивностью, можно определить количество каждой фазы в смеси. Визуальный подбор таких двух линий и составляет сущность метода.

Метод градуировочной кривой. Этот метод позволяет проводить количественный фазовый анализ двухфазной смеси, состоящей из – и β- фаз.

На полученной дифрактограмме выбирают аналитические линии – и β- фазы,

измеряют их интегральную интенсивность, отношение этих интенсивностей и откладывают его на ординате градуировочного графика, а затем находят содержание – фазы в образце.

Метод внутреннего эталона. В случае порошкового образца,

содержащего более двух фаз, если коэффициент ослабления анализируемой фазы отличается от коэффициента ослабления смеси μi ≠μсм. Этот метод основан на сравнении линий анализируемой фазы с интенсивностью линий эталонного вещества известного количества. Добавив к анализируемому порошку определенное количество эталона тоже в виде порошка и тщательно перемешав их, снимают рентгенограмму и находят отношение интенсивностей линий анализируемой фазы и эталона, или через массы.

Также для определения количественного фазового анализа используют метод добавок, метод независимого эталона, метод измерения коэффициента поглощения в образце, метод определения состава фаз.

С помощью рентгеноструктурного анализа можно проводить анализ остаточного аустенита в стали, мартенсита и феррита; определение концентрации углерода в мартенсите; определение границ растворимости двойных сплавов; анализ текстурированных материалов; определение ориентировки плоскости скольжения и плоскости двойникования.

Анализ нарушений кристаллической структуры. Определение зональных напряжений. Пластическая деформация и фазовые превращения, термическая обработка и облучение частицами высоких энергий, неравномерный нагрев и

289

охлаждение, и ряд других процессов приводят к возникновению в кристалле дефектной структуры. Под зональными напряжениями (макронапряжениями или напряжениями 1рода) понимают упругие искажения, уравновешивающиеся в объеме всего изделия или его значительной части. Напряжения определяют по смещению интерференционной линии по углу θ.

Анализ нарушений кристаллической структуры. Определение блоков

мозаики и величины микродеформации. Конечную структуру кристалла после внешних воздействий можно описать с помощью следующей модели (рис. 28.2). Исходный монокристалл разбивается на крупные осколки - кристаллиты,

повернутые друг относительно друга практически на любые углы. Каждый же

участков сжатых, растянутых, изогнутых и т.п. Эти участки кристалла как бы скрепляет клей аморфные или полуаморфные, насыщенные дислокациями участки решетки. Физические свойства такой системы существенно зависят от средних величин размера блоков, угла разориентировки между ними и величины микродеформаций. Эта модель удобна при рассмотрении причин уширения дифракционных линий.

Если размер блоков достаточно мал (меньше 0,1 мкм), это приводит к заметному расширению дебаевских линий на рентгенограмме. Наличие в поликристаллическом образце микродеформаций (т.е. присутствие кристаллов с вариацией периода решетки) также приводит к расширению линий на рентгенограмме.

Если из условий эксперимента можно заведомо вывести заключение о том, что истинное физическое уширение линии (HKL) вызвано или исключительно микродеформациями, или только измельчением блоков мозаики

290