54.Неперервна випадкова величина. Функція розподілу ймовірностей та її властивості. Ймовірність попадання випадкової величини в заданий інтервал.

Неперервною називається випадкова величина, яка може набувати всіх значень з деякого скінченного чи нескінченного інтервалу.

Функцією розподілу ймовірностей F(х) випадкової В Х наз. ймовірність того, що в результаті випробування ця ВВ набуде значення, меншого за деяке фіксоване число х: F(x)=P(X<x), де х є (∞; +∞).

Властивості: 1)значення функції розподілу F(х) належить відрізку 0;1], тобто

2) функції розподілу F(х) неспадна, тобто для довільних х₁ та х₂ з того, що х₁ < х₂ випливає, що F(x₁)≤ F(x₂).

3) Якщо всі можливі значення ВВ належать інтервалу а;b], то: F(x)=0 при х≤а і F(x)=1 при х>b.

4)

5)ймовірність того, що ВВ Х набуде значення з проміжку а;b) дорівнює приросту функції F(х) на цьому проміжку, тобто: P(a≤x<b)=F(b)-F(a).

6)функція розподілу ВВ неперервна зліва, тобто для будь-якого значення х₀:

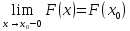
7)функція розподілу може мати не більше, ніж зліченну множину точок розриву першого порядку(стрибків). У кожній точці х_і розриву величина стрибка = різниці F(x_і+0) F(x_і), де F(x_і+0)=.

8)ймовірність того, що неперервна ВВ набуде будь-якого окремого значення а, дорівнює нулю, тобто, якщо Х – неперервна ВВ, то Р(Х=а)=0. 55.Щільність розподілу ймовірностей неперервної випадкової величини та її властивості. Ймовірність попадання в заданий інтервал.

Щільністю розподілу ймовірностей неперервної випадкової величини Х наз. функцію f(x)- першу похідну від функції розподілу F(x), тобто f(x)= F'(x).

Властивості: 1. Це невід’ємна функція: f(x)≥0.

2.Невласний інтеграл від щільності розподілу в межах від ∞ до +∞ дорівнює 1: 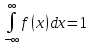, так само і якщо можливі значення ВВ належать інтервалу (а;b).

3.Ймовірність того, що неперервна ВВ Х набуде значення з інтервалу (а;b) дорівнює визначеному інтегралу від щільності розподілу, взятому в межах від а до b: P(a<x<b)=

4.Функція розподілу неперервної ВВ = інтегралу від щільності розподілу на проміжку (∞;х]: F(x)=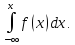 56.Математичне сподівання одновимірної випадкової величини та його властивості.

Математичним сподіванням М(Х) випадкової величини Х називають:

1) Для дискретної ВВ: ,

2)для неперервної ВВ , причому припускається, що ряд і інтеграл збігаються абсолютно.

У цих формулах х_і – значення ВВ, р_і – їх ймовірності, f(x) – щільність ймовірності.

Властивості: 1) М(С)=С, де С=const; 2) М(СХ)=СМ(Х), де С=const; 3) M(X±Y)=M(X)±M(Y), де X і Y – будь-які ВВ; 4) M(XY)=M(X)·M(Y), якщо X і Y – незалежні ВВ. 57.Дисперсія одновимірної випадкової величини. Обчислення дисперсії. Властивості дисперсії. Середнє квадратичне відхилення випадкової величини.

Дисперсією ВВ ( D(X) ) наз. мат. сподівання квадрата різниці ВВ та її мат. сподівання: 1)для дискретної ВВ: , 2)для неперервної ВВ:ОбчислюютьD(X) за формулою:Властивості дисперсії: 1) D(C)=0, де C=const; 2) D(CХ)=С² D(Х), C=const; 3) Якщо X і Y - незалежні ВВ, то Корінь квадратичний з дисперсії наз. середнім квадратичним відхиленням ВВ:Дисперсія і середнє квадратичне відхилення є мірою розсіювання значень ВВ навколо її мат. сподівання. 58.Медіана і мода розподілу.

Модою М₀ дискретної ВВ наз. те її значення х_і, що має найбільшу ймовірність. Модою М₀ неперервної ВВ наз. те її значення х₀, при якому щільність розподілу f(x) цієї величини досягає максимуму, тобто: М₀=х₀, де f(x₀)=max f(x). Геометрично моду можна інтерпретувати як абсцису точки максимуму кривої розподілу. Бувають двомодальні і многомодальні розподіли. Зустрічаються розподіли, які мають мінімум, але не мають максимуму. Такі розподіли наз. антимодальними. Медіаною M_е дискретної ВВ Х наз. те її значення у законі розподілу, для якого сума ймовірностей можливих значень зліва і справа від нього не перевищує 0,5. Медіаною M_е неперервної ВВ наз. те її значення, для якого справедлива рівність: Р(Х< M_е)=Р(Х> M_е)=0,5. Медіану M_е можна знайти з рівняння: F(M_е)=1/2, де F(х)-функція розподілу величини Х. Для дискретної ВВ Х медіана визначається неоднозначно і тому практично не застосовується як числова характеристика. З геометричної точки зору, медіана – це абсциса мочки, в якій площа, обмежена кривою розподілу, ділиться навпіл. Слід відзначити, що якщо розподіл одномодальний і симетричний, то математичне сподівання, мода й медіана співпадають. 59.Початкові і центральні моменти розподілу. Коефіцієнти асиметрії й ексцесу.

Початковим моментом ν_k порядку k випадкової величини Х наз. мат. сподівання ВВ Х^k, тобто: . Центральним моментомµ_k порядку k випадкової величини Х наз. мат. сподівання центрованої ВВ Х(0 над Х) в степені k, тобто:. Центральні моменти виражаються через початкові моменти за формулами:

Центральні моменти характеризують розсіювання ВВ. Асиметрією теоретичного розподілу наз. відношення центрального моменту третього порядку до кубу середнього квадратичного відхилення: де

Асиметрія показує, чи симетричний розподіл відносно центру розподілу(мат. сподівання). Якщо розподіл симетричний відносно мат. сподівання, то A_s=0. Якщо A_s>0, то «довша частина» кривої розподілу розташована справа від М(Х), якщо A_s<0, то «довша частина» кривої розташована зліва від М(Х). Ексцесом ВВ Х наз. величина (для нормального розподілу). ВеличинаE_k характеризує «крутизну» кривої щільності ймовірності в порівнянні з кривою Гаусса. Для гостровершинних кривих E_k>0, для пологих E_k<0. 60.Біноміальний закон розподілу дискретної випадкової величини та його числові характеристики.

Закон розподілу дискретної ВВ наз. біноміальним, якщо ймовірності можливих її значень дорівнюють відповідним членам розкладу бінома (q+p)ⁿ. Його записують у формі таблиці

Нехай проводиться n незалежних випробувань, у кожному з яких подія А може відбутися, або не відбутися. Ймовірність появи події в усіх випробуваннях стала й = p(ймовірність не появи q=1- p). Розглянемо дискретну ВВ Х, яка характеризує число появи події А в n випробуваннях. ДВВ Х при n випробуваннях може набути значень 0,1,2,3,… n з ймовірністю, яку визначають за доп. формули Бернуллі.

Покладаючи у формулі Бернуллі m=0,1,2,… n, будемо мати закон розподілу ВВ Х: число появ події А у n випробуваннях:

Цей закон можна записати у вигляді таблиці:

Для біноміального закону розподілу