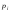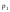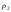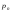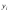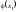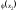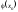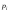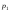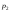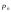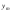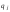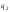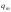- •2. Границя і неперервність функції 2-х змінних.
- •7. Екстремум функції двох змінних. Необхідні і достатні умови екстремуму.
- •12.Однорідні диференціальні рівняння 1 -го порядку.
- •13.Лінійні диференціальні рівняння 1 -го порядку.
- •31.Розвинення в ряд Маклорена функцій.
- •32.Наближене обчислення інтегралів за допомогою рядів.
- •36.Випадкові події. Алгебра подій (сума, різниця, добуток).
- •40.Геометричне означення ймовірності.
- •42.Теорема додавання ймовірностей сумісних подій.
- •44.Ймовірність появи хоча б однієї події з декількох незалежних подій.
- •45.Формула повної ймовірності.
- •50.Асимптотична формула Пуассона.
- •52.Ймовірність відхилення відносної частоти події в серії з n незалежних випробувань від ймовірності події в одному випробуванні.
- •53.Дискретна випадкова величина. Способи її задання. Закон розподілу.
- •54.Неперервна випадкова величина. Функція розподілу ймовірностей та її властивості. Ймовірність попадання випадкової величини в заданий інтервал.
- •61.Розподіл Пуассона та його числові характеристики.
- •62.Рівномірний закон розподілу та його числові характеристики.
- •63.Показниковий розподіл і його числові характеристики.
- •70.Дискретні двовимірні випадкові величини, закон розподілу ймовірностей, основні властивості. Закони розподілу компонент.
- •71.Неперервні двовимірні випадкові величини. Функція розподілу та її властивості.
- •75.Умовне математичне сподівання дискретної і неперервної двовимірної випадкової величини.
- •79.Визначення щільності розподілу функції неперервної випадкової величини по щільності розподілу аргументу.
- •97.Типи статистичних гіпотез. Нульова і конкуруюча гіпотези. Помилки 1 -го і 2-го роду. Рівень значущості.
75.Умовне математичне сподівання дискретної і неперервної двовимірної випадкової величини.
Для дискретної
двовимірної ВВ (X,
Y)
умовні мат. сподівання обчислюються за
формулами:

Для неперервної
двовимірної ВВ:
 76.Залежні
і незалежні випадкові величини. Необхідна
і достатня умова незалежності випадкових
величин.
76.Залежні
і незалежні випадкові величини. Необхідна
і достатня умова незалежності випадкових
величин.
Дві ВВ наз. незалежними, якщо закон розподілу кожної з них не залежить від того, якого значення набула інша. Із цього означення випливає, що умовні розподіли незалежних величин дорівнюють їх безумовним розподілам, тобто:
![]()
Теорема.
Для того, щоб неперервні ВВ X
і Y
були незалежними, необхідно і досить,
щоб функція розподілу системи (X,
Y)
дорівнювала добутку функцій розподілу
складових:
![]()
Наслідок. Для того,
щоб неперервні ВВ X
і Y
були незалежними, необхідно і досить
щоб щільність сумісного розподілу
системи (X,
Y)
дорівнювала добутку щільностей розподілу
складових:
![]()
У випадку, коли X
і Y
– дві незалежні дискретні ВВ, то необхідна
і достатня умова незалежності X
і Y
виражається системою рівностей:
![]() 77.Числові
характеристики двовимірної випадкової
величини. Початкові і центральні моменти.
Кореляційний момент і коефіцієнт
кореляції. Теорема про кореляційний
момент для незалежних випадкових
величин.
77.Числові
характеристики двовимірної випадкової
величини. Початкові і центральні моменти.
Кореляційний момент і коефіцієнт
кореляції. Теорема про кореляційний
момент для незалежних випадкових
величин.
Важливими числовими характеристиками двох ВВ (X, Y) є мат. сподівання та дисперсії складових М(Х), М(Y), D(X), D(Y), кореляційний момент µxy і коефіцієнт кореляції rxy.
Початковим моментом
порядку (k + s) системи (X, Y) наз. мат.
сподівання добутку Xk
· Ys.
![]()
Центральним
моментом порядку (k + s) системи (X, Y) наз.
мат. сподівання k-го і s-го степенів
відповідних центрованих величин.
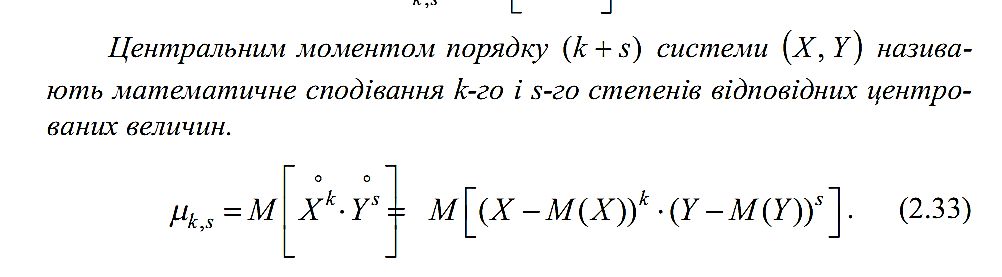
На практиці
найчастіше застосовують початкові
моменти першого порядку та центральні
моменти другого порядку.
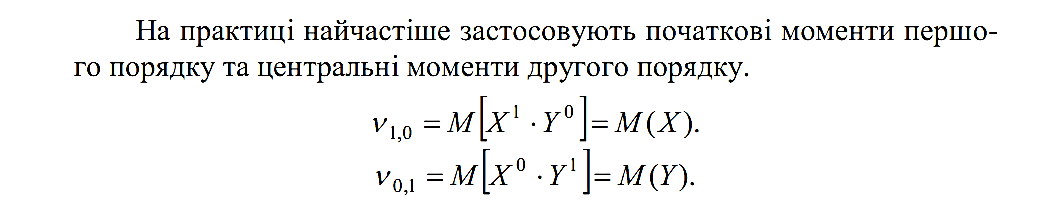
Початкові моменти першого порядку є мат. сподіваннями випадкових величин X і Y.
Центральні моменти
другого порядку співпадають з дисперсіями
випадкових величин X і Y. Вони характеризують
розсіювання системи (X, Y) у напрямку осей
ОХ і ОY.

Особливу роль при
вивченні системи двох ВВ відіграють
другий мішаний центральний момент
![]() і
коефіцієнт кореляції rxy
, які є показниками взаємозв’язку між
компонентами X і Y.
і
коефіцієнт кореляції rxy
, які є показниками взаємозв’язку між
компонентами X і Y.
Кореляційним
моментом (коваріацією) µxy
двовимірної
ВВ (X, Y) наз. мат. сподівання добутку
відхилень складових цієї величини від
мат. сподівань:
![]()
Кореляційний
момент можна виражати співвідношенням:
![]()
Кореляційний момент характеризує як розсіювання величин X і Y, так і зв’язок між ними. Якщо випадкові величини X і Y незалежні, то можна показати, що кореляційний момент µxy = 0 (обернене не має місця).
Випадкові величини, для яких кореляційний момент = 0, наз. некорельованими.
Коефіцієнтом
кореляції rxy
двовимірної
ВВ (X, Y) наз. відношення кореляційного
моменту µxy
до добутку
середніх квадратичних відхилень
![]() цих
величин:
цих
величин:
![]() де
де
![]()
Зазначимо , що
![]() Коефіцієнт
кореляції характеризує ступінь тісноти
лінійної залежності між величинами X і
Y. Чим ближче значення
Коефіцієнт
кореляції характеризує ступінь тісноти
лінійної залежності між величинами X і
Y. Чим ближче значення![]() до
1, тим більш точною буде рівність
до
1, тим більш точною буде рівність![]()
Якщо rxy = 0, то або залежність між X і Y лінійному закону не підлягає, або вони взагалі незалежні.
Числові характеристики
двовимірної ВВ:


Теорема. Кореляційний
момент двох незалежних ВВ Х і Y
дорівнює 0.
Доведення: Так як Х і Y
– незалежні ВВ, то їх відхилення
![]() і
і![]() також незалежні. Користуючись властивостями
мат. сподівання і відхилення, отримаємо:
також незалежні. Користуючись властивостями
мат. сподівання і відхилення, отримаємо:![]() Коваріацію
можна представити у вигляді:
Коваріацію
можна представити у вигляді:
![]() 78.Функція
дискретної випадкової величини. Закон
розподілу функції, числові характеристики.
78.Функція
дискретної випадкової величини. Закон
розподілу функції, числові характеристики.
Важливою задачею в теорії ймовірностей є визначення законів розподілу та числових характеристик функцій випадкових аргументів, закони розподілу яких відомі. Нехай Х — дискретна випадкова величина, яку задано табличним законом розподілу.
|
|
|
|
… |
|
|
|
|
|
… |
|
Відомо,
що
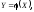 тоді закон розподілуY
має такий вигляд:
тоді закон розподілуY
має такий вигляд:
|
|
|
|
…. |
|
|
|
|
|
… |
|
Числові характеристики функції можна знайти за її законом розподілу або за формулами:
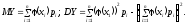
Довільні моменти розподілу подаються аналогічними формулами:

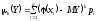 .
.
Якщо
випадкові величини
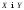 задано законами розподілу:
задано законами розподілу:
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
і задано
функцію
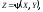 то закон її розподілу визначається так.
Множина значень, що їх набуваєZ,
подається у вигляді:
то закон її розподілу визначається так.
Множина значень, що їх набуваєZ,
подається у вигляді:
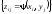 ,
,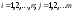 .
При цьому
.
При цьому
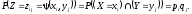
Нехай
Х
— неперервна випадкова величина, яку
задано щільністю розподілу
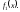 Якщо
Якщо і
— диференційована функція, монотонна
в області значень Х,
то щільність розподілу цієї функції
подається у вигляді
і
— диференційована функція, монотонна
в області значень Х,
то щільність розподілу цієї функції
подається у вигляді
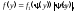 де
де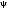 — функція, обернена до.
Якщо
— не монотонна функція в області зміни
аргументу, то обернена функція неоднозначна
і щільність розподілу
— функція, обернена до.
Якщо
— не монотонна функція в області зміни
аргументу, то обернена функція неоднозначна
і щільність розподілу
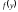 визначається як сума стількох доданків,
скільки значень має обернена функція:
визначається як сума стількох доданків,
скільки значень має обернена функція: де
де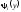 — функції, обернені до.
— функції, обернені до.
Визначаючи числові характеристики функцій неперервних аргументів, операцію підсумовування, виконувану для дискретних величин, заміняють операцією інтегрування: