
- •2 Затухание волн в материальных средах
- •3 Коэффициент распространения.
- •4 Понятие характеристического сопротивления
- •6 Магнитодиэлектрическая среда без потерь
- •7 Электромагнитные волны в средах с частотной дисперсией
- •8 Волновое уравнение
- •9 Распространение радиоволн в земных условиях
- •10 Волны в хорошо проводящей среде
- •11 Распространение электромагнитных волн в бесстолкновительной плазме.
- •12 Интерференция и дифракция электромагнитных волн.
- •13 Дифракция Френеля и Фраунгофера
- •14 Электромагнитные волны в сверхпроводниках.
- •15 Угол Брюстера.Полное внутреннее отражение.
- •16 Замедление электромагнитных волн диэлектрической пластины.
- •17 Поверхносные электромагнитные волны.
- •18 Гребенчатые и другие замедляющие волны.
- •19 Распространение эмв в анизотропной среде.
- •20 Поперечное распространение радиоволн в намагниченном феррите.
- •21 Продольное распространение радиоволн в намагниченном феррите.
- •22 Общие характеристики диапазонов радиоволн.
- •24 Формула идеальной радиосвязи. Множитель ослабления
- •25 Особенности распространения радиоволн различных диапазонов
- •26 Условия излучения
- •27 Зоны Френеля
- •28 Корреляционные замирания
- •29 Искажения сигналов в тракте распространения
- •30 Характеристики источников линий помех
- •31 Распространение укв на наземных радиолиниях.
- •32 Расчет поля в освещенной зоне с учетом рефракции.
- •33 Формула Введенского
- •34 Расчет поля с учетом рельефа местности.
- •35 Распространение укв в городе.
- •36 Устойчивость работы линий связи
- •37 Дальнее тропосферное распространение укв
- •40 Распространение оптических волн
- •39 Распространение дв
- •38 Распространение cв
Рассмотрим
идеализированную задачу о распространении
однородной плоской электромагнитной
волны в неограниченной гиротропной
среде при условии, что волна распространяется
в направлении, перпендикулярном вектору
постоянного подмагничивающего поля
Но - происходит поперечное распространение
волны. Вектор Но ориентирован вдоль
положительного направления оси z.
Предположим, что плоская электромагнитная
волна распространяется вдоль оси х,
так что все проекции векторов поля
имеют комплексные амплитуды,
пропорциональные множителю
Волновой
процесс характеризуется лишь двумя
комплексными амплитудами Hz и Ёу, которые
удовлетворяют системе двух уравнений20 Поперечное распространение радиоволн в намагниченном феррите.
![]() ,
где
,
где![]() —
некоторый коэффициент фазы (продольное
волновое число).
—
некоторый коэффициент фазы (продольное
волновое число).
![]() ,
,![]()
21 Продольное распространение радиоволн в намагниченном феррите.
Плоская
электромагнитная волна распространяется
в неограниченной гиротропной среде
вдоль направления постоянного
подмагничивающего поля. При этом все
проекции векторов поля будут зависеть
от продольной координаты z по закону
![]() ;
выбор знака аргумента комплексной
экспоненты диктуется выбором одного
из двух возможных направлений движения
волновых факторов. Предположим, что
волны однородны в поперечной плоскости
и поэтому
;
выбор знака аргумента комплексной
экспоненты диктуется выбором одного
из двух возможных направлений движения
волновых факторов. Предположим, что
волны однородны в поперечной плоскости
и поэтому![]() .
=> находим, что
.
=> находим, что![]() т.
е. рассматриваемые решения уравнений
Максвелла обязательно являются чисто
поперечными Т-волнами.
т.
е. рассматриваемые решения уравнений
Максвелла обязательно являются чисто
поперечными Т-волнами.
Плоская электромагнитная волна с двумя ортогональными пространственными компонентами, сдвинутыми по фазе на угол 90°, представляет собой волну, поляризованную, по кругу. Таким образом установлено, что при продольном распространении волн в намагниченном феррите существуют две независимые моды:
1)
поляризованная по кругу волна с левым
направлением вращения, у которой
![]() и
коэффициент фазы
и
коэффициент фазы![]()
2) аналогичная волна с правым направлением вращения, у ко-
торой
![]() и
коэффициенты фазы
и
коэффициенты фазы![]()
Теперь предположим, что в какой-либо плоскости, скажем при
z=0,
одновременно возбуждены обе моды с
одинаковыми амплитудами. Тогда в этой
плоскости комплексная амплитуда
суммарного магнитного вектора
![]() ориентирована
вдоль оси х и отвечает линейно
поляризованной волне.
ориентирована
вдоль оси х и отвечает линейно
поляризованной волне.
Обе
моды с круговой поляризацией, из которых
складывается такая волна, распространяются
с разными фазовыми скоростями, и поэтому
в поперечной плоскости с произвольной
координатой z магнитный вектор имеет
комплексную амплитуду
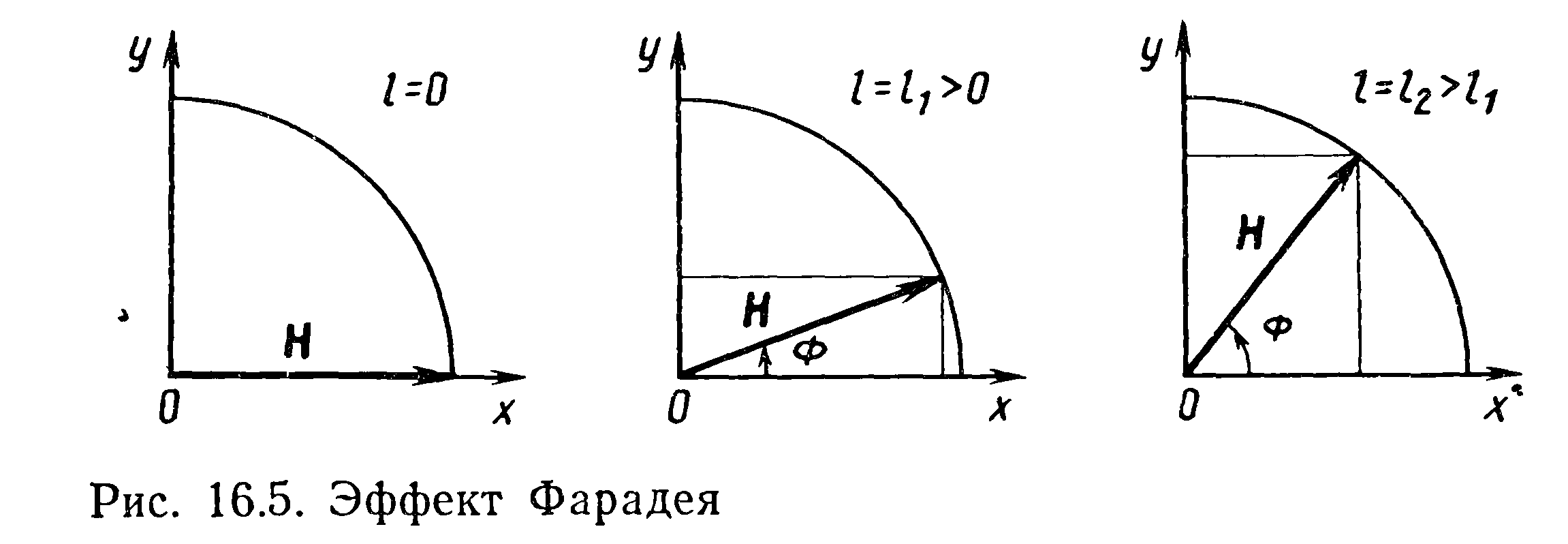
![]()
