Тема 6. Физика колебаний

Колебательные процессы – процессы, характеризующиеся определенной повторяемостью во времени.

Колебания называются свободными (или собственными) если они совершаются за счет первоначально сообщенный энергии при последующем отсутствии внешних воздействий.

Вынужденные колебания совершаются под действием внешней периодически изменяющейся силы, которая называется вынуждающей..

Простейшим типом колебаний являются гармонические колебания – колебания, совершающиеся по закону синуса или косинуса.

х = A sin (t  ); х = A cos (t  ) - уравнение гармонических колебаний

x – смещение - [м] А – амплитуда колебаний - максимальное смещение тела от положения равновесия [м] (t  ) – фаза колебаний – определяет положение колеблющегося тела в любой момент времени

 - круговая или циклическая частота , число полных колебаний за 2 секунд. t – время;

 - начальная фаза – определяет положение колеблющегося тела в начальный момент времени при t = 0.

Кроме того, колебания ёще характеризуются периодом и частотой колебаний.

Т – период - время одного полного колебания ; [с]

[Гц] - частота колебаний – число полных колебаний за 1с.

   - связь между циклической частотой и частотой колебания

Скорость гармонических колебаний определим как производную смещения:

Ускорение

a = - ²x – ускорение гармонических колебаний.

Тогда запишем

- дифференциальное уравнение

гармонических колебаний.

Решением этого уравнения является выражение х = A sin (t  ).

Кинетическая энергия материальной точки, совершающей гармонические колебания

Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F

Тогда полная энергия гармонических колебаний

Полная энергия остается постоянной, так как при гармонических колебаниях справедлив закон сохранения механической энергии, поскольку упругая сила консервативна.

Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида: х + ²х =0

Примерами гармонического осциллятора является пружинный, физический и математические маятники.

Пружинный маятник – это груз массой m, подвешенный на упругой пружине и совершающей гармонические колебания под действием упругой силы

	F = - kx, где k - жесткость пружины период колебаний пружинного маятника Потенциальная энергия пружинного маятника
	Физический маятник – твердое тело, совершающее под действием силы тяжести колебания, вокруг неподвижной оси, не проходящей через центр тяжести. -период колебаний физического маятника. где J - момент инерции, l- расстояние между точкой подвеса и центром тяжести - приведенная длина физического маятника

Тогда

Математический маятник – система, состоящая из материальной точки массой m, подвешенной на нерастяжимой, невесомой нити и колеблющаяся под действием силы F_m.. Момент инерции математического маятника

J = ml2, где l – длина маятника. . период колебаний математического маятника Если L= l, то периоды колебаний одинаковы. Следовательно, приведенная длина физического маятника – эта длина такого математического

маятника,период колебаний которого совпадает с периодом колебаний данного физического маятника.

Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, т.е. колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты.

х₁ = A₁ соs (t  ₁ )

х₂ = A₂ cos (t  ₂)

Тогда уравнение результирующего колебания

х = х₁ + х₂ = A соs (t  )

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает так же гармонические колебания в том же направлении и с той же частотой. Амплитуда результирующего колебания зависит от разности фаз (₂ - ₁) складываемых колебаний.

Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называетсябиением.

Период биений

 - разность частот складываемых колебаний.

Теперь рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимных перпендикулярных направлениях вдоль оси x и y.

Начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю. х = A соs t y = В cos (t  ) Сложив эти два уравнения и сделав преобразования, получим:

- уравнение эллипса

Так, как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.

Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания сложная.

Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно – перпендикулярных колебания, называются фигурами Лиссажу.

Фигуры Лиссажу

Рассмотрим свободные затухающие колебания, амплитуда которых из-за потерь энергии колебательной системой с течением времени уменьшается. Уменьшение энергии происходит вследствие трения в механических колеба-тельных системах и превращение её в теплоту (пружинный маятник).

здесь  = const, - коэффициент затухания.

где r – коэффициент сопротивления.

Решением уравнения в случае малых затуханий (²  ²) является

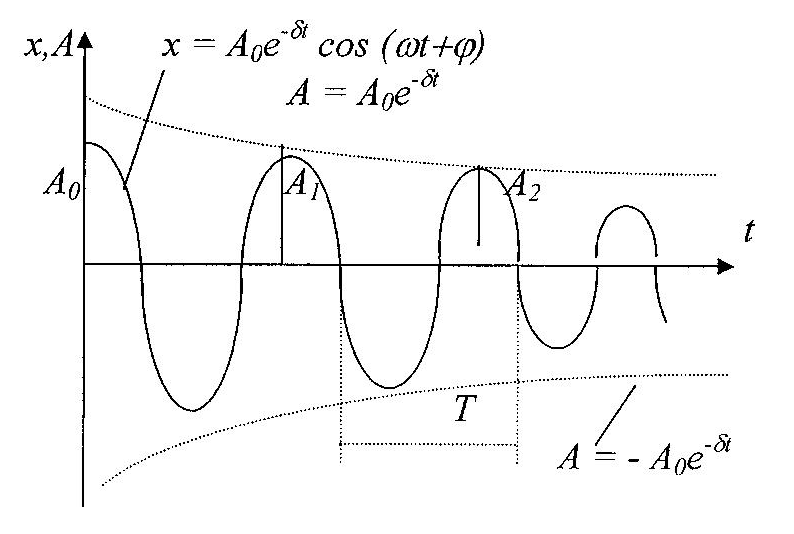
х = А₀е^-t cos (t)

где А = А₀е^-t – амплитуда затухающих колебаний

А₀ – начальная амплитуда.

Промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.

Затухание нарушаетпериодичность колебаний, поэтому затухающие колебания не являются периодическими и к ним не применимо понятие периода или частоты. Если затухание мало, то можно условно пользоваться понятием периода – как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины.

Тогда период затухающих колебаний

ЕслиА(t) и А(t+T) - амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающихся на период, то отношение

- декремент затухания, а его логарифм

- логарифмический декремент затухания

N_e – число колебаний, совершаемых за время уменьшения амплитуды в е раз.

Чтобы получить в реальной колебательной системе незатухающие колебания, надо компенсировать потери энергии.

В случае механических колебаний нужна внешняя вынуждающая сила F = F₀ cost. Тогда уравнение вынужденных колебаний

где

Решение уравнения равно сумме решения однородного уравнения и частного решения

В установившемся режиме вынужденные колебания происходят с частотой  и являются гармоническими колебаниями Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты . Амплитуда вынужденных колебаний определяется по формуле: .

Чтобы определить резонансную частоту _рез – частоту, при которой амплитуда достигает максимума – нужно найти максимальную функцию или минимальную подкоренного выражения. Продифференцировав подкоренное выражение по частоте, получим:

_рез =

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте называют резонансом.

При ²  ₀², значение резонансной частоты _рез совпадает с _0, тогда