3.2 Методи трансформації гравітаційних полів

Більшість трансформацій потенціальних полів чисельно виконують за алгоритмом лінійної згортки двох дискретних функцій. Перша функція – значення спостереженого поля. Друга – аналітична функція, яка визначається в межах заданого вікна трансформації. При обробці профільних спостережень вікном трансформації є інтервал профілю, визначений певною кількістю точок спостережень; площинних – коло або прямокутник (частіше квадрат), розміри якого теж визначаються певною кількістю точок спостережень. Як правило, вікно у декілька разів менше за профіль чи площу спостережень. За межами вікна аналітична функція є нульовою. Трансформацію розраховують як суму добутків аналітичної функції й значень поля в межах вікна. Значення суми, тобто результат трансформації поля, присвоюється тій точці спостережень, яка є центром вікна. Кожний раз після розрахунків вікно послідовно переміщується по профілю (площі) із сталим кроком, який дорівнює кроку спостережень. На початку і в кінці профілю, або по краю площі спостережень, вікно “виходить” за їхні межі, що спотворює трансформацію. Є різні способи послаблення спотворень у межах крайових зон, розмірами до половини вікна. Простіше, коли є можливість не враховувати ці зони у подальшій інтерпретації трансформованих полів.

Трансформація методом осередненнявиконується з метою виділення регіональних аномалій зі спостереженого поля.

Спостережене поле сили тяжіння в редукції Буге є сумою двох основних складових:

, (3.6)

де - регіональна складова,

- локальні аномалії.

Регіональну складову наближено можна представити осередненим полем.

Осереднення поля, спостереженого на площині, визначають у межах кола радіусом R за формулою:

, (3.7)

де - початок координат, розташований у центрі кола.

Трансформація осереднення підкреслює аномалії, які плавно змінюються по площі, та вилучає або послабляє аномалії з різкими градієнтами.

Для найкращого виділення регіональних аномалій розмір вікна осереднення (2R) повинен бути меншим за їхні розміри, але більшим за розміри локальних аномалій, які необхідно або вилучити з поля, або суттєво послабити в трансформованому полі. При виконанні цих умов:

. (3.8)

Локальні аномалії отримують як різницю:

. (3.9)

Міра осередненняаномалій:

. (3.10)

Міра осереднення одночасно характеризує і степінь точності виділення локальних аномалій. Для локальних геологічних об’єктів (наприклад, подібних до кулі) установлено наступну залежність між мірою та глибиною їхнього залягання:

, (3.11)

де .

Для об’єктів інших форм – це максимальна оцінка можливої глибини залягання =.

Вираз (3.11) дає можливість визначити радіус осереднення R, якщо задана необхідна точність виділення локальних аномалій та глибина залягання пошукових геологічних об’єктів.

Вибір радіуса осереднення за оцінкою глибини залягання геологічних утворень не завжди є оптимальним, оскільки розміри аномалій залежать і від горизонтальних розмірів цих геологічних утворень та інших факторів.

Частіше радіус осереднення R вибирають емпірично (дивись п.3.1). Якщо визначений радіус осереднення і відома глибина залягання джерел локальних аномалій, то можна оцінити міру точності їх виділення.

У практиці програмування часто використовують не кругову, а квадратну палетку (вікно), для якої формула (3.7) у декартовій системі координат:

, (3.12)

де - розміри сторін квадрата (вікна трансформації).

Міра осереднення для квадрата:

, (3.13)

де .

Інтервал можливих значень = 0,1 0,6.

Трансформація осереднення для профілю:

(3.14)

2nx – довжина вікнатрансформації;

x – крок спостережень по профілю.

Локальні аномалії визначають як різницю полів:

(3.15)

Залежність між розмірами вікна осереднення L = 2nx та глибиною залягання геологічних утворень, аномалії від яких необхідно виділити у спостереженому полі, неоднозначна. У більшості випадків L  (26)h_ℓ , де h_ℓ – передбачувана глибина залягання локальних пошукових об’єктів. Для витягнутих структур – L  (12)h_ℓ.

Трансформація методом згладжування знижує рівень випадкових завад (похибок спостережень) і аномалій малого порядку, що сприяє більш чіткому проявленню шуканих локальних аномалій. Суть методу полягає в апроксимації спостереженого поля алгебраїчним поліномом у межах вікна. Розміри вікна вибираються за апріорними даними про загальний характер розподілу локальних або регіональних аномалій. Найпростішим варіантом згладжування є осереднення, який полягає в заміні спостереженого поля середнім значенням у межах вікна трансформації (згладжування поліномом нульової степені). Для згладжування, як правило, використовують поліном другого або третього ступеня. Поліном другого ступеня має вигляд:

, (3.16)

де b₀, b₁, b₂ – коефіцієнти полінома.

З метою послаблення помилок спостережень виконують згладжування поля за способом Маловічко О.К. із малим вікном у 5-ть точок:

(3.17)

де x₀ – точка спостережень по профілю, що є центральною у вікні.

Визначене значення згладженого поля присвоюється точці x₀. Далі розрахунки проводять для наступної точки x₀+x, яка буде центральною вікна трансформації, і так далі.

Якщо крок спостережень x становить менше 1/4 від передбаченої глибини залягання геологічних утворень, то спотворенням корисних аномалій поля при згладжуванні можна нехтувати (воно становить не більше 1%). Як правило, на практиці дана умова виконується. Збільшення вікна трансформації призводить до згладжування не тільки похибок спостережень, але й аномалій, розміри яких є меншими заданого вікна.

В наступних формулах згладжування за різними розмірами вікна наведений коефіцієнт середнього послаблення таких аномалій (коефіцієнт згладжування Q).

Згладжування з вікном у 13 точок:

(3.18)

Q = 0,39.

Згладжування з вікном у 21 точку:

(3.19)

Q = 0,30.

Важливим питанням є вибір довжини вікна трансформації. Воно змінюється зі зміною кроку вибірки значень поля по профілю. Зрозуміло, що крок вибірки може дорівнювати, наприклад, 2x, 3x і так далі. Від розміру вікна залежить ступінь згладжування аномального поля. Як уже було сказано, для визначення розмірів вікна можна орієнтуватись на передбачені розміри корисних аномалій. Дослідним шляхом установлено, що довжина вікна повинна бути дещо меншою або дорівнювати розмірам корисних аномалій. При наявності геологічних утворень, близьких за формою до антиклінальних структур, довжина вікна повинна приблизно дорівнювати або бути дещо меншою лінійних розмірів структур.

Згладжування аномалій буде тим більше чим менше їхні розміри та більше вікно трансформації.

По площі згладжування проводиться по вісі х, потім - по вісі у.

Трансформації згладжування й осереднення близькі за змістом. Тому згладжування можна використати для виділення аномалій певного порядку, якщо провести згладжування за двома розмірами вікна, Перше згладжування, наприклад, може бути за способом Маловічко О.К. Локальні аномалії певного порядку можна отримати за різницею цих двох трансформацій. Лінійні розміри виділених таким чином аномалій будуть більшими за вікно першої трансформації і меншими другої. За змістом вони можуть відповідати геологічним утворенням, що залягають у певній смузі глибин. А різниця трансформацій є так званою комбінованою трансформацією.

Трансформація за методом Гриффіна (Андреєва)дозволяє виділяти локальні аномалії безпосередньо зі спостереженого поля:

, (3.20)

де - середнє значення поля по колу з радіусом,

центр якого в точці x,y.

За цим методом аномалії від геологічних об’єктів, що розташовані на глибинах , послабляються на 50% i більше.

Метод Гриффіна, який пристосований для перетворень полів по профілю, називається способом Андреєва.

За способом Андреєва локальні аномалії визначаються:

, (3.21)

де та- значення поля в рівновіддалених точках на профілі відносно центральної точкиx₀,

d– відстань, яка є радіусом вікна трансформації.

Для виділення корисних аномалій вікно трансформації (2d) повинно бути менше лінійних розмірів цих аномалій.

Трансформація за методом Саксова-Нiгардадозволяє виділяти аномалії, джерела яких розташовані в межах певної смуги глибин. Вона виконується за формулою:

, (3.22)

де – осереднені градієнти;

та - осереднені значення поля вздовж кіл,

що мають радіуси та;

центри кіл із радіусами розташовані в точціx,y.

Аномалії джерел ізометричної форми будуть виділені найкращим чином, коли [4]:

2=, (3.23)

де z– відома глибина залягання джерел;

–=;

–досить мала величина, наприклад, дорівнює кроку

спостережень.

Якщо радіус трансформації зменшувати, то інтенсивність аномалії осереднених градієнтів теж буде зменшуватись до нуля. Якщо радіус трансформації збільшувати, то аномалія осереднених градієнтів буде спотворена впливом інших, бокових геологічних утворень.

При неточних даних про глибини залягання джерел поля смугу –слід розширювати. В цілому співвідношення радіусів бажане наступне:

; , (3.24)

де - оцінка глибини залягання об’єктів.

У трансформованому полі менше за інші будуть послаблені аномалії від об’єктів, глибина залягання яких:

. (3.25)

Перерахунок гравітаційних аномалій у верхній і нижній півпростір.

Сутність розділення аномалій при продовженні поля у півпростори наступна. Зі зростанням відстані від джерел аномалії зменшуються в залежності від глибини залягання джерел та їхніх розмірів. Аномалії дрібних об’єктів, що неглибоко залягають, зменшуються швидше; аномалії об’єктів, що є більшими за розмірами та залягають на більших глибинах, послабляються повільніше. На більшій відстані від об’єктів зберігається загальний характер поля, деталі ж зникають. З наближенням до об’єктів, в полі проявляються деталі, які на великих відстанях непомітні. Таке явище схоже на дію оптичної лінзи при зміні відстані до об’єкта, що досліджується.

Способи аналітичного продовження розрізняються тільки чисельними прийомами рішення інтеграла Пуассона, за яким здійснюється перерахунок поля у верхній півпростір.

Для перерахунку аномалій у верхній півпростір по профілю спостережень використовується спосіб, розроблений Андреєвим Б.О.:

, (3.26)

де x₀ – координата точки по профілю, для якої розраховується

поле U_h(x₀) на висоті h;

U(x₀) – значення поля на профілі спостережень у точці x₀

(z=0);

х_h – інтервал інтегрування (сумування), який виражений в

одиницях h,

тобто ;

;

;

;

;

-m+m –вікно трансформації, яке виражене в кількості точок

вибірки значень поля з інтервалом x;

- залишковий член, що

зменшує похибку трансформації, зумовлену

обмеженістю інтервалу інтегрування.

Профіль розбивається на кроки інтегрування х таким чином, щоб у межах кроку поле змінювалось приблизно за лінійним законом (дуже часто – це крок спостережень).

Як правило, інтервал інтегрування:

.

Найбільш простим та розповсюдженим на практиці способом перерахунку гравітаційних аномалій у нижній півпростір є спосіб сіток. У двовимірному випадку значення аномалії у довільній точці профілю x₀ на глибині h (вісь z направлена вниз) розраховується за формулою:

, (3.27)

де - спостережене значення поля по профілюz=0

у точці x₀;

- спостережене значення поля

в точці з координатою ;

- значення поля, перераховане на висоту h

у точці x_0;

- спостережене значення поля

в точці з координатою .

Таким чином перед перерахунком поля за методом сіток на глибину h необхідно спочатку розрахувати поле на відповідній висоті h, наприклад, за способом, що описаний за формулою 3.26.

При перерахунку полів униз необхідно пам’ятати, що перерахунок полів можливий лише доти, поки глибина перерахунку залишається вище особливих точок по розрізу (точки зламу границь, центри тяжіння геологічних утворень). Інакше розрахунок буде неправильним, оскільки при переході через поверхню локальних джерел поля змінюються за іншими законами, а в особливих точках мають розрив.

Перед перерахунком униз краще всього наближено оцінити глибину залягання джерел корисних аномалій – h_а, далі спостережене поле згладити з вікном, що дещо менше передбачуваних лінійних розмірів корисних аномалій, а перерахунок униз виконати на глибину дещо меншу ніж h_а.

Перерахунок поля у верхній півпростір у тривимірному випадку можна виконати за способом, розробленим Маловічко О.К.:

, (3.28)

де ,;

- радіуси кіл, по яким визначаються середні значення

поля ;

розрахункова точка є центром кіл;

-коефіцієнти, значення яких наведені в таблиці 3.1.

Таблиця 3.1–Значення коефіцієнтів приM = 7

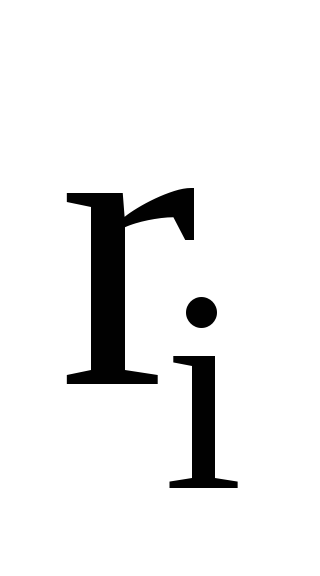
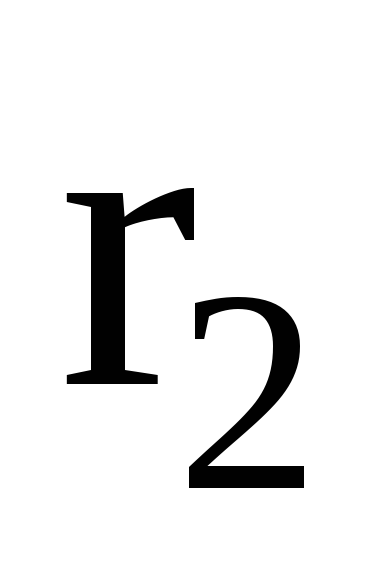
	0.1464	0.2764	0.1954	0.1024

Продовження таблиці 3.1

	0.0600	0.0390	0.0270	0.0202

Як правило, для задовільного наближення достатньо M = 5. Розмірами вікна трансформації є максимальний радіус . Для отримання поля на висоті центр вікна переміщується по всіх точках, в яких мають бути підраховані значення перетвореного поля.

Локальні аномалії визначають як різницю:

, (3.29)

Перерахунок поля у нижній півпростір у двовимірному випадку (за Веселовим Н.Е.):

, (3.30)

де ;

–ряд біноміальних коефіцієнтів;

- значення поля по профілю z=0у точках , початок

координат у центрі вікна трансформації, розмірами

L=.

Перерахунок поля у нижній півпростір у тривимірному випадку (за Веселовим Н.Е.):

, (3.31)

де

;

- середні значення поля по колу радіусом ,

центр якого в розрахунковій точці.

Обмеження на M (розмір радіуса вікна трансформації) або N (обмеження на кількість членів біноміального ряду) визначають підчас розрахунків за значеннями чергового члена ряду (ряди збіжні), для останнього члена попередньо задають певне достатнє обмеження. Як правило, M та N  10.

За технологією розрахунків алгоритми перерахунку уверх та вниз тотожні. Для продовження поля униз рекомендують виконати попереднє згладжування, наприклад, за способом Маловічко О.К.

Перерахунок гравітаційних аномалій у треті похідні потенціалу. З теорії гравітаційного потенціалу відомо, що спостережене поле сили тяжіння є першою вертикальною похідною гравітаційного потенціалу:

(3.32)

Відповідно третя похідна:

(3.33)

Перерахунок поля у треті похідні потенціалу розповсюджений у практиці інтерпретації. За параметрами аномалій третьої похідної потенціалу можна оцінювати глибини залягання геологічних утворень (у тому числі й антиклінальних структур).

Нижче вибірково наведені формули В.М.Берьозкіна, які розрізняються кількістю точок значень поля у вікні М і відповідно різним рівнем зростання випадкових похибок перетворення Q.

При М = 5:

(3.34)

2L = (M-1)x; Q = 2,14.

При М = 21:

(3.35)

Q = 1,33.

Результат перерахунку залежить від розміру вікна диференціювання 2L. Для підвищення вірогідності перерахунку бажано вікно диференціювання вибирати в межах:

2L = (0.5  2)h_а, (3.36)

де h_а – оцінка глибини залягання пошукових геологічних

утворень.

Питання для самоперевірки

1) Перелік основних трансформацій потенційних полів і їх призначення.

2) Задачі, що розв’язуються за допомогою трансформацій.

3) Проблеми, пов’язані з використанням трансформацій.

4) Варіанти отримання локальних аномалій.

5) Вікно трансформації. Алгоритм трансформації.

6) Залежність між параметрами трансформацій, спостереженим і трансформованим полем. Відповіді надати прикладами.

7) Залежність між геологічними задачами та вибором трансформації і її параметрів.

Література

1. Миронов В.С. Курс гравиразведки. Л-д.: Недра, 1972, -512с.

2. Березкин В.М. Применение гравиразведки для поисков месторождений нефти и газа. М., Недра, 1973, -264с.

3. Успенский Д.Г. Гравиразведка. Л-д.: Недра, 1968, -332с.

4. Грушинский Н.П., Сажина Н.Б. Гравитационная разведка. М., Недра, 1972, -390с.