
- •ВВЕДЕНИЕ
- •1.2. Классификация кинематических пар
- •1.3. Основные виды механизмов и их структурные схемы
- •1.4. Определение степени подвижности механизма
- •РАЗДЕЛ 2. КИНЕМАТИКА
- •2.1. Кинематика точки
- •2.2. Кинематика твердого тела
- •2.3. Плоское движение твердого тела
- •2.4. Кинематика механизмов
- •РАЗДЕЛ 3. ДИНАМИКА
- •3.1. Основные законы динамики
- •3.2. Связи и реакции связей
- •3.3. Силы трения
- •3.4. Центр масс и моменты инерции материальной системы
- •3.5. Общие теоремы динамики
- •РАЗДЕЛ 4. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАШИНЫ
- •4.1. Расчет машинного агрегата
- •4.2. Уравнение движения механизма в дифференциальной форме
- •4.3. Снижение периодических колебаний угловой скорости машины
- •5.1. Схематизация формы элементов конструкций
- •5.2. Внутренние силы в элементах конструкций. Метод сечений
- •5.3. Механические напряжения в материале. Нормальные и касательные напряжения
- •5.4. Диаграмма растяжения малоуглеродистой стали. Закон Гука.
- •5.5. Допускаемые напряжения и общая методика расчетов на прочность
- •5.6. Расчет элементов конструкций при растяжении (сжатии)
- •5.7. Геометрические характеристики поперечных сечений
- •5.8. Расчет элементов конструкций при чистом сдвиге и кручении
- •5.9. Расчет элементов конструкций при чистом изгибе
- •ЗАКЛЮЧЕНИЕ
- •Библиографический список
- •Предметный указатель
- •ОГЛАВЛЕНИЕ
- •Учебное пособие
116 |
|
||
N x l |
≤[ |
l] |
|
E A |
|||
|
|
||
и позволяет решить также ряд задач: проверить на жесткость, найти требуемое поперечное сечение, оценить допускаемые продольные силы [6], [11].
5.7. Геометрические характеристики поперечных сечений
Напряжения зависят от сил, моментов сил и геометрии поперечных сечений. Понятия геометрические характеристики поперечных сечений, к которым относят форму, величину площади, положение центра тяжести, статические моменты, моменты инерции и моменты сопротивления сечения потребуются при расчетах на прочность.
Всякое тело можно рассматривать состоящим из большого числа малых частиц, на которые воздействуют силы тяжести. Равнодействующую этих сил называют силой тяжести. Точка приложения этой равнодействующей при различных положениях тела называют центром тяжести тела.
Координаты x0 и y0 центра тяжести плоской фигуры определяются формулами
|
|
A |
∫ |
|
|
A ∫ |
|
|
|
x0 |
= |
1 |
|
xdA , |
y0 = |
1 |
|
y dA , |
(5.1) |
|
|
|
|
||||||
|
|
|
(A) |
|
|
(A) |
|
||
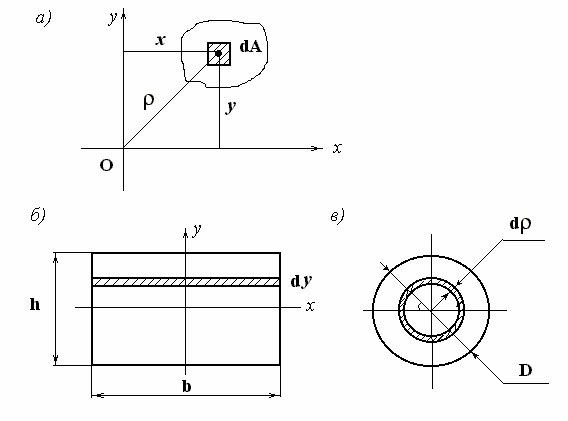
где А – площадь фигуры; |
dA – элемент этой площади (рис. 5.11, а). |
|
|||||||
Интегралы |
|
|
|
|
|
|
|
|
|
S x = ∫y dA = A y0 , |
S y = |
∫x dA = A x0 |
(5.2) |
||||||
(A) |
|
|
|
|
|
(A) |
|
|
|
называют статическими моментами фигуры относительно осей x и |
y . Оси |
||||||||
проходящие через центр тяжести, называют центральными, а статические моменты инерции относительно центральных осей равны нулю.
117
Рис. 5.11
Моменты инерции делятся на осевые, полярные и центробежные.
Осевым моментом инерции называют взятую по всей площади сечения сумму произведений элементарных площадок на квадраты их расстояния до соответствующей оси
I x = ∫y 2 dA , |
I y = ∫x2 dA. |
(5.3) |
(A) |
(A) |
|
Полярным моментом инерции (момент инерции относительно полюса p )
называют взятую по всей площади сумму произведений элементарных
площадок на квадраты их расстояний до данного полюса (рис. 5.11,а) |
|
|
I p = ∫ρ2 dA = ∫(x2 + y 2 )dA = I y + I x . |
(5.4) |
|
(A) |
(A) |
|
Центробежным моментом инерции называют взятую по всей площади сечения сумму произведений элементарных площадок на произведения обеих координат

118
I xy = ∫x y dA. |
(5.5) |
(A) |
|
Оси, проходящие через центры тяжести, относительно которых I xy = 0,
называются главными центральными осями инерции сечения.
Можно доказать, что ось, перпендикулярная оси симметрии, проходящая через центр тяжести лежащая в плоскости фигуры, будет другой главной центральной осью инерции. Для круга и кольца любые две взаимно перпендикулярные оси, точка пересечения которых совпадает с их центром тяжести, являются главными центральными осями инерции.
В общем случае главные и центральные оси могут быть найдены, если известны ценробежный и осевой моменты инерции фигуры относительно произвольных центральных осей. Для этого необходимо систему осей x , y
повернуть на угол α, определяемый соотношением
tq 2α = |
2I x y |
(5.6) |
|||
I y |
−I x . |
||||
|
|
1 |
1 |
|
|
|
1 |
|
1 |
|
|
Моменты инерции относительно главных центральных осей инерции называются главными моментами инерции. Они обладают тем свойством, что один из них имеет максимальное, а другой – минимальное значения по сравнению с моментами инерции относительно других центральных осей.
I max = |
1 |
(I x |
+ I y |
)± |
1 |
(I x |
− I y )2 +4I xy2 . |
(5.7) |
|
2 |
2 |
||||||||
min |
1 |
1 |
|
1 |
1 |
|
|||
|
|
|
|
|
Значения моментов инерции фигур, а также прокатных профилей (уголков, двутавров, швеллеров) приводятся в справочной литературе. Например, для прямоугольного сечения главные моменты инерции равны
I x = |
bh3 |
, I y = |
b3 h |
, |
(5.8) |
|
12 |
12 |
|||||
|
|
|
|
где b – ширина; h – высота (рис. 5.11, б).

|
|
119 |
|
|
|
|
|
|
Для кольца с наружным D и внутренним d |
диаметрами осевые моменты |
|||||||
равны |
|
|
|
|
|
|
|
|
I x = I y = π(D4 −d 4 ) |
0,05D4 (1−k 4 ), |
k = |
d |
, |
(5.9) |
|||
D |
||||||||
а полярный момент инерции |
64 |
|
|
|
|
|
||
π(D4 −d 4 ) 0,1 D4 |
|
|
|
|
|
|||
I p = |
(1−k 4 ). |
|
|
|
(5.10) |
|||
|
32 |
|
|
|
|
|
|
|
В таблицах справочников встречается радиус инерции, который определяется по формуле
ix = |
I |
x |
или iy = |
I y |
; |
ip = |
I p |
. |
(5.11) |
|
A |
A |
A |
||||||||
|
|
|
|
|
|
|||||
При анализе сложных сечений учитывается, что момент инерции фигуры относительно некоторой оси x1 , параллельной главной центральной оси и отстоящей от нее на расстоянии a , равен
I x = I x + A a2 . |
(5.12) |
1 |
|
Кроме выше отмеченных используются осевые и полярные моменты сопротивления сечений, которые определяются отношением соответствующих моментов инерции к координатам наиболее удаленных от оси или полюса точек, то есть
W |
x |
= |
I |
x |
, |
W |
|
= |
I y |
, |
W |
|
= |
I p |
. |
(5.13) |
|
|
y |
xmax |
p |
ρmax |
|||||||||||
|
|
ymax |
|
|
|
|
|
|
|
|||||||
Эти величины для прямоугольного сечения |
|
|
|
|
|
|
||||||||||
|
|
|
Wx = |
bh |
2 |
, |
Wy = |
b2 h |
. |
|
|
(5.14) |
||||
|
|
|
2 |
|
12 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Перечисленные геометрические характеристики сечений будут использованы при расчетах элементов конструкций на прочность и жесткость.
5.8.Расчет элементов конструкций при чистом сдвиге и кручении
5.8.1.Напряжения и деформации при чистом сдвиге
120
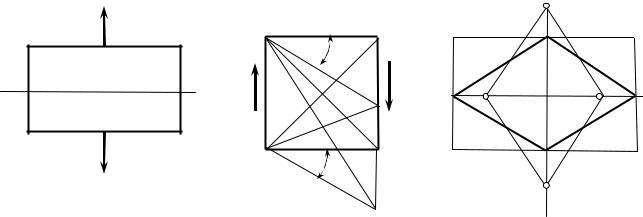
Сдвиг – это вид деформации, при котором возникают две противоположные направленные силы F в близко расположенных параллельных плоскостях перпендикулярно оси бруса (рис. 5.12, а). При этом происходит относительное смещение сечений, характеризуемое углом сдвига. Сопротивление такому сдвигу обуславливает появление в вертикальных плоскостях сечений касательных напряжений τ. Разрушение при сдвиге называется срезом.
а) |
б) |
в) |
F |
A |
|
|
C |
|
|
C |
C′ |
|
|
|
γ |
C′ |
|
|
|
|
|
|
τ |
O |
O |
τ |
B′ |
B |
O |
D |
D′ |
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
B |
γ |
|
D |
|
|
|
′ |
|
|
F |
|
|
|
|
|
|
A |
|
|
|
|
|
|
D′ |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.12
Чистым сдвигом называют деформацию, обусловленную действием только касательных напряжений в сечении. При чистом сдвиге квадратный элемент ABCD после приложения по его сторонам касательных напряжений превращается в ромб ABC′D′ (рис. 5.12, б) с углами при вершинах, равными
соответственно π2 +γ и π2 −γ , где γ – угол сдвига. Исходя из закона Гука,
можно записать τ = G γ, где – модуль сдвига (числовые значения модуля при-
водится в справочниках для различных материалов).
Установим связь между сдвигом и растяжением и сжатием. Если совместить фигуры недеформированного состояния (квадрат) с деформированным состоянием (ромб) (рис. 5.12, в), то получим, что при сдвиге произошло

121
удлинение диагонали AC и укорочение диагонали BD на одну и ту же
величину |
ВВ′ = СС′. Это следует из рассмотрения треугольников АСС′ и |
||||||||||||||||
BDD′ (рис. 5.12, б). Относительные деформации половин этих диагоналей |
|||||||||||||||||
обозначим через ε1 и ε3 , тогда |
|
|
|
|
|
|
|
|
|
|
|||||||
ε1 = |
ОВ′−ОВ |
= |
BB′ |
; ε3 = |
ОС′−ОС |
= − |
CC′ |
; ε1 = |
|
ε3 |
|
= ε; ε1 = −ε3 . |
|||||
|
|
||||||||||||||||
|
|
|
|
||||||||||||||
|
ОВ |
OB |
|
|
|
|
ОС |
|
OC |
|
|
|
|
||||
|
|
|
′ |
′ |
имеем |
|
|
|
|
|
|
|
|
|
|
||
Из треугольника OB C |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 π |
|
OC −CC′ |
1 −ε |
|||||||||
|
|
|
tq |
2 2 − γ |
|
= OB + BB′ |
= 1 + ε . |
||||||||||
Разлагая в ряд последнее выражение и учитывая малость деформаций
( tq γ/ 2 γ/ 2), получим
γ/ 2 = ε = ε1 = −ε3 .
Сдругой стороны для достижения деформированного состояния в виде ромба и при отсутствии сдвигающих сил F необходимо приложить нормальные силы для растяжения диагонали BD и сжатия диагонали AC силы F вдоль BD (растяжение σ1 ) и вдоль AC (сжатие σ3 ). Вследствие
одинаковости деформаций σ1 = σ3 , а для сохранения тех же касательных
напряжений в наклонных площадках под углом 45o должны выполняться pавенства
|
σ1 = −σ3 = 2 τ. |
|
|
|
|
(5.15) |
||||||
Общее удлинение диагонали BD состоит из продольной деформации ε1′ от |
||||||||||||
σ1 и поперечной деформации ε1′′ |
от σ3 , то есть |
|
|
|
|
|
||||||
ε1 = ε1′ + ε1′′ = |
σ |
|
|
|
σ |
3 |
|
1 |
|
(σ1 |
−νσ3 ). |
|
1 |
+ ν − |
|
= |
|
|
(5.16) |
||||||
|
E |
|||||||||||
|
E |
|
|
E |
|
|
|
|
|
|||
Аналогично для диагонали AC : |
|
|
|
|
|
|
|
|
|
|
||
ε3 = ε′3 + ε′3′ = |
σ |
3 |
|
σ |
|
|
1 |
|
(σ3 |
−νσ1 ). |
|
|
|
+ − |
|
1 |
|
ν = |
|
|
(5.17) |
||||
|
|
E |
|
|||||||||
|
E |
|
E |
|
|
|
|
|
|
|||

122
Полученные выражения для ε1 и ε3 дают обобщенный закон Гука при двух-
осном растяжении-сжатии. Записав закон Гука для растяжения и сдвига с учетом (5.16) – (5.17), получим
ε1 E1 (σ1 −νσ3 )= σE1 (1+ ν)= 2Eτ(1+ ν)= γ = Gτ .
Откуда
E = 2G (1 + ν).
Это соотношение дает связь трех основных упругих констант материала: модуля упругости, модуля сдвига G и коэффициента Пуассона ν . Из этого выражения следует, что для сталей модуль сдвига примерно в 2,6 раза меньше модуля упругости.
Следует отметить, что при сдвиге происходит только изменение формы, а изменение объема отсутствует.
5.8.2. Практические расчеты элементов конструкций на сдвиг
На сдвиг рассчитываются соединения деталей машин и приборов, которые делятся на разъемные и неразъемные. К разъемным соединениям относятся: болтовые, шлицевые, резьбовые; а к неразъемным – сварные, заклепочные, клеевые, прессовые.
Условие прочности при сдвиге (срезе) записывается
τрасч ≤ [τ],
где τрасч , [τ]– расчетное и допускаемое напряжения при сдвиге (срезе).
Допускаемое напряжение [τ] на сдвиг (срез) принимается обычно в зависимости от допускаемого напряжения на растяжение
[τ]= ϕ[σ]р ,
где ϕ = 0,5K0,8– опытный коэффициент, зависящий от типа и условий работы и конструкции.
Проблема заключается в нахождении распределения нагрузок по элементам (болтам, заклепкам, сварным швам и т.п.). Так, например, еще Н.Е. Жуковский
123
показал, что осевая нагрузка по виткам резьбы распределяется неравномерно, при этом первый виток воспринимается примерно 50%, а второй – 25%, а шестой – 2%. Ошибки изготовления и износ резьбы искажают эту картину и затрудняют определение истинных нагрузок. Аналогичная ситуация возникает при расчете болтовых, заклепочных и сварных соединений.
Для упрощенных расчетов предполагается, что нагрузка распределяется по элементам соединений равномерно, а при действии в плоскости стыков моментов сил предполагается абсолютная жесткость стыков или соединений, что позволяет использовать условие пропорциональности нагрузок на каждый болт их расстояниям от центра поворота. Эти же предположения используются при расчете коротких сварных швов.
Наиболее опасными повреждениями крепежных и ходовых резьб является срез резьб по их цилиндрической поверхности с внутренним диаметром d1 для болта и наружным диаметром d для гайки. Ориентировочная проверка резьбы на срез сводится к сравнению осевой нагрузки с допускаемой соответственно для болта и гайки:
F |
≤[F]= πd |
кН |
|
[τ] |
, |
|
|
|
|||||
б |
1 |
|
г |
кнр |
||
F |
≤[F]= πd кН |
|
[τ] |
, |
||
|
|
|||||
г |
|
|
г |
кнр |
||
где Нг – высота гайки; к – коэффициент полноты резьбы, равный 0,87 для |
||||||
треугольной, 0,65 для трапецевидной, 0,5 для прямоугольной резьб; кнр – коэф-
фициент, учитывающий неравномерность распределения нагрузки среди витков и равный 1,3. . .1,5 при σ / σ >1,3 и 1,65. . .1,80 при . Допускаемые касательные напряжения [τ]= 0,2...0,3σy .
При загрузке болтов поперечной силой Q , что имеет место при их установке без зазора (фланцевые муфты, обоймы зубчатой муфты), их проверяют на срез по формуле

124
τ = |
4Q |
≤[τ], |
|
|
|
||
|
πd02 n0 |
|
|
где d0 – диаметр стержня болта в месте среза; |
n0 – число плоскостей среза, |
||
[τ]= 0,4σт при постоянной нагрузке и [τ]= 0,2σт |
при переменной. |
||
Угловые швы сварных соединений рассчитывают на срез по опасному сечению (наименьшему), расчетное значение которого принимается 0,7к, где
к – катет шва, по формуле
τ = 0,7Qкl ≤[τ],
где Q – перерезывающая сила; l – длина шва; [τ]= 0,6[σ]р для ручной сварки электродами Э42, Э50 и [τ]= 0,65[σ]сж для других видов сварки.
Заклепочные соединения обычно загружены силами, действующими в плоскости стыка. При этом заклепку рассчитывают также как болт, поставленный без зазора.
5.8.3. Напряжения и деформации при кручении бруса круглого поперечного сечения
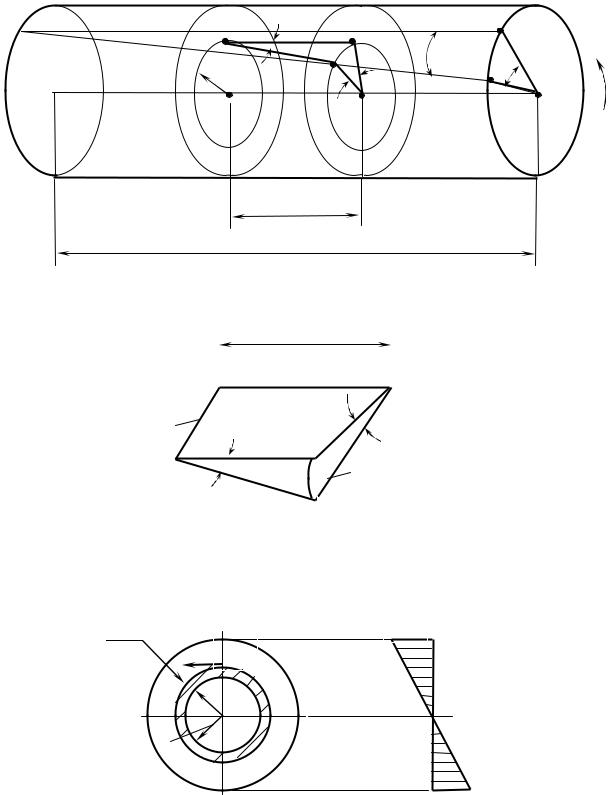
Кручение – вид деформации, при которой в каждом поперечном сечении силовым фактором является крутящий момент. При кручении полагается, что сечения остаются плоскими и перпендикулярными к продольной оси x , расстояния между сечениями не изменяются, а радиусы в сечениях не искривляются. Исходя из этих предположений, деформация элемента получит относительный поворот, характеризуемый углом ϕ вокруг оси
(рис. 5.13, а). Образующая СА1 цилиндра максимального радиуса r займет положение СА2 . Угол между образующими недеформированного и дефор-
мированного состояний обозначим через γ . Если вырезать горизонтальной плоскостью элемент dx радиуса ρ(рис. 5.13, б) до деформации О1О2 В1 В2 , то

125
после деформации он развернется относительно О1 В1 на расстояние В2 В2′ при этом B2O2 B2′ = dϕ, а B2 B1B2′ = γ (рис. 5.13, б).
Из геометрии получаем
В2 В2′ =ρ dϕ= γ dx
откуда
γ = ρ ddxϕ.
Деформация кручения обусловлена действием крутящего момента Tx ,
характеризуемая чистым сдвигом на угол, который изменяется от 0 до γ , то есть кручение представляет собой неоднородный сдвиг. Касательные напряжения τТ и угол сдвига γ связаны законом Гука
τТ = G γ =Gρ ddxϕ .
Сечение находится в равновесии при действии крутящего момента Tx и
внутренних моментов сил τТ ρ dА. Из равенства сил получим dTx = τТ ρ dА.
После интегрирования по площади поперечного сечения получим
Тx = ∫d Tx = ∫τT ρ d A = G |
dϕ |
∫ |
ρ |
2 |
dA = G I p |
dϕ |
, |
|||||
dx |
|
dx |
||||||||||
(A) |
(A) |
|
|
|
|
(A) |
|
|
|
|
|
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dϕ |
= |
Tx ρ |
|
|
|
|
|
|
|
|
|
|
dx |
G I p |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
Напряжения при кручении будут равны
а)
C 
б)
в)
126
B1 |
γ |
B2 |
A2 |
Tx |
|
B2′ |
γ |
ϕ |
|
e |
dϕ |
A1 |
|
|
O1 |
ρ |
O2 |
r |
O |
dx
l
dx
O1 |
|
|
O2 |
|
|
||
ρ |
B2 |
dϕ |
|
B1 |
|
||
|
ρ |
||
|
γ |
||
|
|
|
|
|
B2′ |
|
|
dρ |
τT |
|
τT |
O
ρ 

Рис. 5.13

|
127 |
|
|
|
τТ |
= |
Тх ρ |
, |
(5.18) |
|
||||
|
|
G I p |
|
|
где I p – полярный момент инерции.
Графическое изображение распределения напряжений в сечении называется эпюрой напряжений. Как видно из выражения (5.18) (рис. 5.13, в), касательные напряжения сплошного сечения при ρ = r достигают максимального значения
τT max = |
Tx |
= |
|
Tx |
, |
I p / r |
|
||||
|
|
Wp |
|||
где Wp = I p / r (см. раздел 5.3.2), |
и минимального значения на оси бруса |
||||
τT min = 0 .
В сечении касательные напряжения распределены по линейному закону. Поэтому применение кольцевых сечений более рационально с точки зрения экономии материала, при этом значение максимальных касательных напряжений примут вид
τmax = (Tx− 4 ),
Wp 1 c
d
где с = d1 , d , d1 – диаметры внешнего и внутреннего сечений бруса.
Угол закручивания бруса на длине l определяется после интегрирования выражения
dϕ = |
Tx |
dx |
или ϕ = |
Tx l |
. |
|
|||||
|
|
||||
|
G I p |
|
G I p |
||
Основным элементом конструкции машин, работающих на кручение, является вал, вращающийся с угловой скоростью ω и передающий мощность N . При отсутствии других силовых факторов условие прочности имеет вид
τт ≤[τ].
128
Допускаемое напряжение [τ] при статической нагрузке принимается равным
[τ]= 0,5...0,6 [σ], а |
[σ]= |
σт |
, где σт – предел текучести; n – допускаемый |
|
|
[n] |
|
коэффициент безопасности.
5.8.3.1. Практические расчеты на прочность и жесткость при кручении
При проектном расчете валов обычно определяют их диаметры. Валы изготавливают из углеродистых и легированных сталей: Ст.5 – для валов без термообработки; Ст. 45 или Ст.45Х – для валов с термообработкой; Ст.45ХН, Ст.30ХГСА – для высоконапряженных валов ответственных машин. Диаметр вала определяется из выражения
d ≥ 3 |
Tx |
N |
||
|
= 3 |
|
. |
|
0,2[τ] |
0,2 ω[τ] |
|||
Обычно эта формула записывается в упрощенном виде
d ≥ 3 cT ; c = 0,21[τ].
Для валов редукторов без специальных требований по весу и габаритам принимают c = 400 , а для валов трансмиссий – с =100 .
Главным критерием работоспособности валов является крутильная
l
жесткость G Iр , которая обеспечивается выбором длины, диаметра и
материала в соответствии с выражением для ϕ, определяющего жесткость вала
ϕ = Тx l ,
G Iр
где G I р – жесткость вала, отнесенная к единице длины l .
При расчетах на жесткость ϕ≤[ϕ], который выбирают в зависимости от назначения вала и его размеров. Для валов средних размеров допускаемый угол закручивания равен 0,5o на 1 м длины.
