98

деформированной оси бруса приводит к новой модели деформирования, более точно отражающей реальность.

Исходя из выше изложенного, определяют следующие виды деформаций бруса:

1)осевое растяжение (сжатие) – деформация, при которой все продольные волокна получают одинаковое удлинение (укорочение) с одновременным уменьшением (увеличением) поперечных размеров; плоские сечения при этом перемещаются вдоль продольной оси параллельно самим себе;

2)кручение – деформация, сопровождающаяся относительным поворотом поперечных сечений бруса вокруг продольной оси; расстояния точек сечений до этой оси остается неизменным;

3)изгиб – деформация, при которой происходит искривление продольной оси бруса.

5.2. Внутренние силы в элементах конструкций. Метод сечений

При деформациях элементов конструкций возникают дополнительные межмолекулярные силы, стремящиеся вернуть их в первоначальное состояние. Эти силы называются внутренними, которые и определяют прочность элементов конструкций.

Для определения внутренних сил используется метод сечений. Реализация метода сечений заключается в следующем.

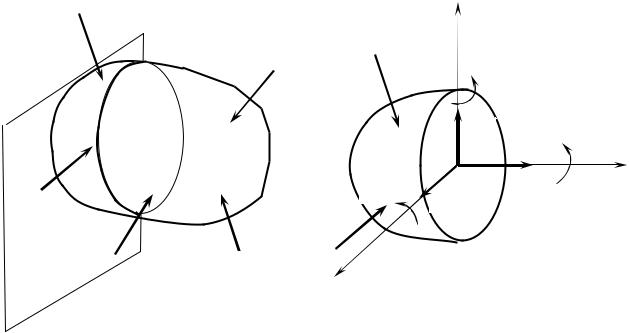
1. Расчетная модель элемента конструкции со всеми приложенными к ней нагрузками и реакциями связей мысленно рассекается плоскостью Q в

заданном месте на две независимые части (рис. 5.4, а).

2. В сечении принимается система координат с началом в центре тяжести сечения, ось x по нормали к сечению, а оси y и z , совпадающие с его главными центральными осями инерции лежат в плоскости сечения.

99

3. Мысленно отбрасывается одна из этих частей, а ее воздействие на оставленную часть характеризуется внутренними силами: их главным вектором

Rr и главным моментом Мr в сечении.

4. Проекции главного вектора R и главного момента М на координатные оси

(рис. 5.4, б) имеют следующие обозначения и наименования: Rx = N x –

продольная сила; Ry = Qy ; Rz =Qz – поперечные силы; M x =Tx – крутящий момент; M y = M y ; M z = M z – изгибающие моменты.

Проекции главного вектора и главного момента сил называются силовыми факторами. Эти силовые факторы обуславливают соответствующие деформации: N x – растяжение или сжатие; Qy , Qz – сдвиг; M y , M z – изгиб;

Tx – кручение.

5. Внутренние силовые факторы определяются из условий статического равновесия рассматриваемой части.

Рис. 5.4

5.2.1.Построение эпюр

Вкачестве примера рассмотрим расчетную схему тихоходного вала редуктора (коробки передач) как более нагруженного (рис. 5.5, а), где вал

101

обозначен прямой линией (ось вала), левая шарнирно-неподвижная и правая шарнирно-подвижная опоры моделируют подшипники качения, к зубчатому колесу с делительным диаметром d приложены сосредоточенные силы в зацеплении: Ft – окружная, Fr – радиальная и Fa – осевая, приложенные в точке зацепления, положение и величина которых полагается известными. Заметим, что эти силы, внутренние для зубчатых колес в зацеплении являются внешними для выделенного вала с колесами.

Вводится неподвижная система декартовых координат с началом на левой опоре. Влияние шарнирных опор заменяются реакциями в них (рис. 5.5, б),

параллельно самой себе и заменяется силой Ft , действующей перпендикулярно

изгибающего момента M x = Fa d / 2 , действующего относительно оси z .

Реактивные составляющие опорных реакций определяются из условий равновесия, которые примут вид:

∑ПрхF = Rx1 + Fa = 0; откуда Rx1 = −Fa ;

∑Прy F = Ry1 + Ry2 −Fr = 0;

∑Прz F = Rz1 + Rz2 + Ft = 0 ;

∑M x (F )=Tx = Ft d2 = 0;

∑M y (F )= Ft a + Rz2 (a +b)= 0;

∑M x (F )= Fr a + Fa d2 −Ry2 (a +b)= 0.

Четвертое уравнение проекций моментов относительно оси x не содержит реакций и при холостом вращении выходного вала крутящий момент равен нулю, при нагружении выходного вала крутящий момент Tx обеспечивает

102

выполнение технологического процесса (в коробке передач этот крутящий момент предназначен для вращения колес).

Для определения внутренних сил система делится на грузовые участки. Грузовым участком называется участок элемента конструкции, на котором внешние силы постоянны. В данном случае на два грузовых участка I и II (рис. 5.5, г). На каждом грузовом участке система рассекается на две части, влияние отброшенной правой части характеризуется внутренними силовыми факторами: продольной силой N x , поперечными силами Qy , Qz , изгиба-

ющими моментами M y , M z и крутящим моментом Tx , приложенными к сече-

нию левой части (рис. 5.5, в). Эти факторы определяются из условий равновесия рассматриваемой части.

Для первого сечения (рис. 5.5, г)

грузовой участок 0 ≤ x ≤ a .

На втором грузовом участке (рис.5.5, г) внутренние силы примут вид: 0 ≤ x ≤ a +b , грузовой участок 0 ≤ x ≤ a +b .

103

Из решения следует, что часть силовых факторов ( N x , Qy , Qz , Tx ) явля-

ются кусочно-постоянными, а часть ( M y , M z ) – кусочно-линейными функ-

циями координаты x . Графическое изображение распределения силовых факторов по оси бруса (вдоль оси x ) называется эпюрой. Такие эпюры представлены на рис. 5.5, д. Эпюры позволяют наглядно представить, каким силовым факторам подвержен тот или иной участок и в каких сечениях сочетание этих факторов наиболее неблагоприятно. Последние сечения называются опасными, и именно они в дальнейшем подвергаются анализу. Например, на среднем участке (в месте посадки зубчатого колеса на вал) действуют сжимающая и поперечная силы, изгибающий и крутящий моменты. Вследствие этих факторов участок сжат, подвергается сдвигу по осям y и z ,

изгибу в плоскостях xy , xz и кручению вокруг оси х. На его границах

имеется наиболее неблагоприятное сочетание этих факторов, то есть среднее сечение под зубчатым колесом является опасным.

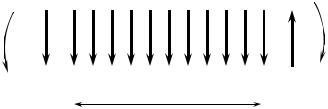
Для проверки правильности построения эпюр и их анализу существенную помощь оказывают дифференциальные зависимости между силовыми факторами. Вырежем элементарный участок бруса с бесконечно малой длиной dx , нагруженный распределенной нагрузкой с интенсивность q y (рис.6.6)

Тогда в крайних сечениях элемента будут действовать силовые факторы Qy ,

M z , Qy +dQy , M z +d M z соответственно. d y (x)

Рис. 5.6

Составляя условия равновесия участка, получим