Тема 3. Системи числення. Арифметичні дії над числами в двійковій системі числення

1. Системи числення.

Приклад. Для обробки будь-якої інформації величини, що характеризують цю інформацію, повинні бути представлені в якомусь виді, найчастіше їх представляють в ЕОМ у вигляді електричних сигналів (напруг). Для представлення інформації існують аналогова (неперервна) і числова (дискретна) форма.

Дискретна інформація може бути представлена в вигляді різних рівнів (по амплітуді) напруг у вигляді звичної для нас десяткової системи числення з цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; або у вигляді двійкової системи з цифрами 0, 1. Ці системи ще називають позиційними системами числення.

Дійсно, числа в таких системах представляють у виді групи порозрядної послідовності цифр, для цілої і дробної частини:

а₂ ∙ а₁ ∙ а_{0 ,} а_-1 ∙ а_-2 ∙ а_-3 … _, (1.1.)

ціла дробна

де а₂ - число сотень;

а₁ - число десятків;

а₀ - число одиниць;

а_-1 - десяткове значення одиниці;

а_-2 - соте значення одиниці;

а_-3 – тисячне значення одиниць.

Одиниці кожного розряду відповідає вага р^к, де р – основа системи числення, к – номер розряду, що визначає позицію числа (одиниці, десятки і т.д.).

Кількість одиниць N, записано в (1.1.) визначається як

N=…+а₂∙р²+а₁∙р¹+а₀∙р⁰+а_-1∙р^-1+а_-2∙р^-2 , (1.2.)

Наприклад 321,135₍₁₀₎ можна записати як

3х10²+2х10¹+1х10⁰+1х10^-1+3х10^-2+5х10^-3=321,135

де ₍₁₀₎ - основа розглянутого числа в десятковій системі числення.

В мікропроцесорній техніці використовується двійкова, вісімкова, шістнадцяткова системи числення.

В двійковій системі р=2(0,1)

Число 11011,101₍₂₎=1∙2⁴+1∙2³+0∙2²+1∙2¹+1∙2⁰+1∙2^-1+0∙2^-2+1∙2^-3= =27,625₍₁₀₎

В вісімковій системі числення : р = 8 (0,1,2,3,4,5,6,7)

33,5₍₈₎ = 3х8¹+3х8⁰+5х8^-1 = 27,125₍₁₀₎

В шістнадцятковій системі числення р=16 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, E, F)

число В9, С2₍₁₆₎ =11х16¹+9х16⁰+12х16^-1+2х16^-2=176+9+0,75+ 0,00781 =185,75781₍₁₀₎

Найбільш просто обробляти і зберігати дані, представлені в двійковій системі числення. Крім такої форми існує ще і двійково-кодована система та інші.

2. Перевід чисел з одної системи числення в іншу.

Перевід будь-якого числа з двійкової системи числення у вісімкову та шістнадцяткову системи проводиться так. Основою вісімкової системи числення являється число 8=2³, то для переводу двійкових чисел у вісімкові необхідно розділити двійкові числа на трьох–бітові групи – тріади і перевести кожну тріаду в десяткове число.

Аналогічно здійснюється перевід двійкових чисел в шістнадцяткові (16=2⁴). В цьому випадку двійкове число розбивається на 4^х-бітові групи (тетради), які і переводяться в шістьнадцяткову цифру. Розбивка двійкового числа на тріади, тетради здійснюється зправа наліво, починаючи з наймолодшого розряду числа. Якщо в групі немає 0 чи 1, групу (старший значущий розряд) доповнюють нулями.

Наприклад, число 11 01 01 0001 110₍₂₎

представляємо, як

001 101 010 001 110₍₂₎ =15216₍₈₎

або

1 5 2 1 6 ₍₈₎

Для переводу вказаного двійкового числа в шістнадцяткову систему числення, це двійкове число розбиваємо по 4 біти:

0001 1010 1000 1110₍₂₎=1А 8D₍₁₆₎

1 А 8 D₍₁₆₎

Дробну частину двійкового слова також можна представити 8 або 16 еквівалентом. Тільки об’єднання в групи по 3 або 4, відповідно, необхідно проводити, починаючи з старшого значущого розряду після десяткової крапки.

Для переводу будь-якого десяткового числа в 2, 8, 16 систему числення, необхідно ділити це десяткове число на основу (2, чи 8, чи 16) системи, в яку ми це десяткове число переводимо, врахувавши залишок.

Наприклад: числа 134 ₍₁₀₎ перевести у двійкову систему числення

Крок Ділення Частка Залишок

1 134:2 67 0-молодший

значущий розряд

2 67:2 33 1

3 33:2 16 1

4 16:2 8 0

5 8:2 4 0

6 4:2 2 0

7 2:2 1 0

8 1:2 0 1-старший

значущий розряд

Результат 134₍₁₀₎=1000 0110₍₂₎

Приклад 2:

Число 634₁₀ перевести у вісімкову систему числення

Крок Ділення Частка Залишок

1 634:8 79 2-м.з.р.

2 79:8 9 7

3 9 : 8 1 1

4 1 : 8 0 1-ст. з.р.

результат: 634₍₁₀₎ = 1172₍₈₎

Приклад 3:

Число 634₍₁₀₎ – перевести в шістьнадцяткову систему числення

Крок Ділення Частка Залишок

1 634 : 16 39 10₁₀ = А₁₆ м.з.р.

2 39 : 16 2 7

3 2 : 16 0 2 ст.з.р.

результат 634₍₁₀₎ = 27А ₍₁₆₎

При переводі дробної частини десяткового числа в а-б-в -2, 8, 16 систему числення, необхідно це дробне число помножити на (а) –2, (б) – 8, (в) - 16 і відповідно:

а) записати 1, якщо число >1, 0 якщо число < 1;

б) заокругливши до цілого числа, якщо числа <8;

в) заокругливши до цілого числа.

Числа, що обробляються в обчислювальних пристроях можуть бути представлені у формі з фіксованою і плаваючою крапкою.

В комірці для зберігання двійкового числа з фіксованою крапкою один розряд (крайній зліва) використовується у вигляді знакового. В ньому записується 0 у випадку додатного, 1 в випадку від’ємного значення числа. Крапка, що розмежовує цілу частину числа від його дробної частини займає фіксоване положення.

Форма з плаваючою точкою передбачає представлення числа в показниковій формі.

Наприклад, число 685,23₁₀ = 0,68523х10³,

де 0,68523 – мантиса;

10 – основа десяткової системи;

3 – порядок.

Ці числа записуються у двійковій формі у вище наведеному порядку.

Ці форми запису необхідні для проведення арифметичних операцій над двійковими числами з заданим степенем точності.

3. Виконання арифметичних операцій.

Основною операцією, яка виконується в цифрових пристроях при різних обчисленнях, є операція алгебраїчного додавання чисел, (додавання, в якому можуть брати участь як додатні, так і від’ємні числа). Віднімання легко замінити операцією додавання, шляхом зміни знаку і величини від’ємника, використовуючи додатковий код. Операції множення та ділення виконуються також з допомогою операцій додавання і деяких логічних дій.

Арифметичні операції можуть виконуватись з високою точністю, з довжиною більше одного слова. Використання арифметики чисел з плаваючою точкою (крапкою) забезпечує роботу пристроїв з дуже великими або дуже малими цифрами.

В дальнійшому знак числа буде виділено

Цифрою 0 – для додатнього числа,

Цифрою 1 – для від’ємного числа.

Операції над числами будемо проводити так, і в такій послідовності, як їх проводить операційний пристрій (суматор процесорного елемента).

3.3.1. Додавання додатніх двійкових чисел

Операції обробки над числами починаються з дій над розміщеними в крайній зправа позиції. Якщо результат додавання найменших значущих цифр двох доданків не поміщається у відповідному розряді результату, то проходить перенос. Цифра, яка переноситься в сусідній зліва розряд, додається до вмісту останнього. Перенос в старший розряд відбувається тоді, якщо результат додавання одноіменних розрядів більше 1 в двійковій системі числення (більше 9 в 10- тій).

МП оперує 8 – розрядними словами (байтами, що складаються з нулів і одиниць), додавання проводиться, починаючи з наймолодшого розряду в результаті сумування двох одиниць наймолодшого розряду (див. приклад) буде 0 і перенос 1 в старший розряд, таким чином, починаючи з 2-го розряду, сумуються три цифри: дві відповідних доданків і перенесена 1 з попереднього розряду. Сумування проводиться розряд з розрядом до найстаршого розряду.

+		ДОДАНОК 1
		0	1
перевірка Д О Д А Н О К 2	0	0	1
	1	1	0 перенос 1 ←

3.3.2. Віднімання додатніх двійкових чисел.

Двійкове віднімання подібне десятковому відніманню.

Якщо вміст розряду зменшуваного, див. табл., менше вмісту одноіменного розряду від’ємника, то результат (клітинка з фоном) визначається шляхом позички з сусіднього старшого розряду.

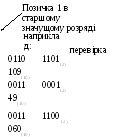
-		Від’ємник
		0	1
З М Е Н Ш У В А Н Е	0	0	1
	1	1	0

3.3.3. Віднімання двійкових кодів в додатковому коді

Представлений спосіб віднімання тяжко реалізувати на ЕОМ, навіть для додатніх цілих чисел. У випадку дробних чисел такий спосіб віднімання практично не реалізують. Віднімання реалізують представивши попередньо число від’ємника безпосередньо знаком і величиною, тобто використавши додатковий код. В двійковій системі додатковий код чисел, що віднімають, формується шляхом інвертування (заміною 0 на 1 і 1 на 0) всіх цифр розрядів, крім знакового, і в молодший розряд добавляється одиниця. Для одержання результату замість віднімання проводиться операція додавання зменшуваного з додатковим кодом від’ємника.

Приклад:

А операція віднімання реалізована через додатковий код:

0011 0001

1 1001 0011

1 1100 0100 ₍₂₎ = ?

Якщо результат зі знаком 1 (-), - то одержимо результат також в додатковому коді.

Реальний результат віднімання, це число в додатковому коді, яке треба ще раз перетворити.

Додатковий код числа 11000100 буде:

00111011

+1

00111100=00111100₍₂₎=-60₍₁₀₎

Не треба забувати правило, якщо в результаті операції віднімання через додатковий код на місці знакового розряду стоїть 1 (-), то одержаний результат треба ще раз перетворити через додатковий код.

Якщо на місці знакового розряду буде 0 (+), то одержаний результат і буде шуканим.

3.3.4. Множення двійкових чисел

Операція множення чисел у формі з фіксованою крапкою включає в себе знаходження знаку і абсолютного значення добутку. Добуток проводиться згідно з табл.

х		множене		Приклад: 0 0 0 1 1 1 0 0 0 0 0 0 1 добуток 0 0 0 0 . зсув на 1 р і 2 добуток 0 0 0 1 . . зсув на 2 і 3 добуток 0 0 0 1 . . зсув на 3 розр. і 4 добуток перенос результат - 0001100(2) або 1/х/12(10) = 12(10)
		0	1
М Н О Ж Н И К	0	0	0
	1	0	1

Спосіб множення здійснюється шляхом находження копії множеного, зсуву “здвигу” і додавання часткових добутків

Правила:

1. Формування 1-го часткового добутку

Якщо значення молодшого значущого розряду множника дорівнює Ø, то і результат дорівнює Ø, якщо значення цього розряду множника рівне 1, то результат є копією множеного.

2. Правило зсуву: При використанні чергового розряду множника для формування часткового добутку здійснюється зсув множеного на один розряд (позицію) вліво.

3. Правило. Кожний раз, коли значення розряду множника дорівнює 1, до результату необхідно добавити множене, яке розміщене в позиції, визначеній правилом зсуву.

4. Знаходження результуючого

Шуканий добуток є результат виконання всіх операцій зсуву і операцій додавання.

3.3.5. Ділення двійкових чисел

Розглянемо спосіб алгебраїчного ділення чисел, представлених у формі з фіксованою крапкою. Ділення - операція, зворотня множенню.

Розглянемо ділення двох чисел 204₍₁₀₎ і 12₍₁₀₎ або

11001100₍₂₎ і 1100₍₂₎

204 12 1217 84 84 0

11001100 1100 110010001 01 0 011 0 110 0 1100 1100 0

Виконати таку операцію так в ЕОМ непросто.

При діленні необхідно визначити, скільки разів дільник вкладається в числі, утвореному відповідною кількістю старших значущих бітів діленого. Мікропроцесор не вгадує, скільки разів дільник укладається в вказаному числі, а в дійсності МП починає віднімати дільник з цього числа через операцію додавання з додатковим кодом.

Якщо дільник не буде вкладатися в названій частині дільника, завжди можна повернути біти, що віднімаються, зворотньо діленому. В тому, що дільник не вкладається, свідчить поява від'ємного результату віднімання (біт знаку різниці дорівнює 1).

Для реалізації операції ділення в процесорах використовується, як і при відніманні, додатковий код для представлення дільника 12₍₁₀₎=(0100)₂ і операції зсуву, як при множенні.

0011(2) – зворотній код 12(10) + 1 0100 – додатковий код 12(10)

Додатковий код числа 12 (0100) буде 11010 (1 – мінус, щоб реалізувати операцію віднімання при діленні необхідно врахувати (-) при відніманні, що реалізується проставленням 1 на місці знакового розряду)

• Перший крок ділення: виконується як операція додавання дільника з додатковим кодом дільника

Якщо дільник вкладається у відповідну частину діленого (знак результату 0), значить результат ділення додатнє число, в даному випадку перший біт результату дорівнює 1.

Другий крок ділення можна робити, попередньо зсунувши перший результат. Зсув повинен бути таким, щоб при наступній операції віднімання (додавання з додатковим кодом) був зформований другий біт частки.

0 00001100 - перший результат до зсуву

0 0001100 - перший результат після зсуву

Другий крок ділення: На 1 розряд менше

0001100 10100000 10101100

- зсунутий перший результат - число 12 в додатковому коді - 2-й результат

Наявність 1 означає, що 2 біт шуканої частки дорівнює 0 і що одержане число від’ємне, дільник не вкладається в відповідну частину діленого, крім того, віднімання не сталось, тому біти дільника необхідно повернути першому результату

10101100 01100000 00001100

- другий результат - повернуте число 12(10) - зсунутий 1-й результат, одержаний повторно (за 2 рази)

Тепер робимо другий зсув

0000100 0001100

зсунутий перший результат перший результат після другого зсуву

Третя операція

0001100 1010000 3 біт результату 0 1011100	дворазово зсунутий результат зменшуване число 12 - третій результат
1011100 0110000 0001100	третій результат повернуте число 12 дворазово зсунутий перший результат

Третій зсув

0001100 001100	дворазово зсунутий перший результат перший результат після 3 зсуву
001100 101000 110100 110100 011000 01100 4 зсув 001100 01100 і остання дія 01100 10100 00000 10001(2) = 17(10)	- перший результат після 3 зсуву - віднімане число 12 - четвертий результат 0, тому - четвертий результат необхідно знову просумувати повернуте число 12 перший результат після 3 зсуву - перший результат після 3 зсуву - результат четвертого зсуву число 12 віднімане число 12 п’ятий результат, наявність 0 означає, що п'ятий біт результату дорівнює 1 - загальний результат ділення

Для арифметичних дій з підвищеною точністю необхідне представлення чисел значно більших розмірів, у такій формі, щоб процесор міг працювати з ними. В процесорах 8-розрядних, використовуючи для даних два восьмибітові слова, тому можна записати від - 32768 до 32767 цифр з помилкою в = 0,0015 %

Для обробки дробних чисел використовується арифметика чисел з плаваючою крапкою (комою), що дозволяє мікропроцесору відслідкувати положення десяткової крапки. Для цього використовується пакет спеціальних програм.

Завдання на графічно-розрахункову роботу по темі 3.

1. Число № 1 (код групи) і число № 2 (номер залікової книжки), записані в десятковій системі числення, перевести з десяткової системи числення в двійкову, вісімкову і шістьнадцяткові системи числення.

Результат перевірити, шляхом зворотнього переводу одержаних чисел в десяткову систему числення.

2. Числа № 1 і № 2, записані в двійковій системі числення, додати, відняти, помножити, поділити між собою. Результат обчислення перевірити шляхом переводу одержаного двійкового числа, що повинно відповідати результатам арифметичних дій над десятковими числами, в десяткову систему числення.

При операціях віднімання, ділення використати додатковий код.