
- •Глава 21. Теоретические представления химической кинетики
- •21.1. Элементарная теория активных столкновений для бимолекулярных реакций
- •21.2. Мономолекулярные реакции
- •21.3. Теория активированного комплекса (переходного состояния)
- •21.3.1. Поверхность потенциальной энергии
- •21.3.2. Основное уравнение теории активированного комплекса
- •21.3.3. Свободная энергия активации
- •21.3.4. Сравнение теорий активных столкновений и переходного состояния
- •21.4. Реакции в растворах
21.3.3. Свободная энергия активации
Константа равновесия реакции, протекающей при постоянном давлении, связана с изменением изобарно-изотермического потенциала (энергии Гиббса) уравнением (11.20). В том случае, когда реагирующие вещества находятся в стандартном состоянии, для реакции образования активного комплекса можно записать:
G#= –RTlnK#, (21.46)
где G#– изменение энергии Гиббса при переходе системы из исходного состояния в активное.
Так как по уравнению Гиббса – Гельмгольца
G#=Н# –ТS#, (21.47)
то для константы равновесия получим:
![]() , (21.48)
, (21.48)
а константа скорости реакции (уравнение (21.45)) будет равна
![]() , (21.49)
, (21.49)
где H#иS#представляют собой теплоту и энтропию активации.
Уравнение (21.49) показывает, что скорость реакции определяется не теплотой активации, а изменением энергии Гиббса активации G# (илиF# для реакций при постоянном объеме), т.е. существенное влияние на скорость реакции может оказывать изменение энтропииS#, увеличение которой способствует повышению скорости.
Сравнение уравнения (21.49) с уравнением Аррениуса (20.98) или уравнением теории соударений (21.14) указывает на их сходство, если положить, что теплота активации H# соответствует энергии активацииE. Связь между ними можно установить следующим образом. Прологарифмируем уравнение (21.44):
![]() . (21.50)
. (21.50)
Дифференцирование его по температуре и сравнение с уравнением Аррениуса дает:
![]() . (21.51)
. (21.51)
Зависимость K#от температуры определяется изобарой Вант-Гоффа (11.26)
![]() . (21.52)
. (21.52)
Таким образом, мы получаем
![]() , (21.53)
, (21.53)
откуда следует связь между экспериментальной энергией активации EA и теплотой активации:
EA = Н#+RT. (21.54)
При умеренных температурах RT<<H#и практически можно считать, чтоEA=H#.
21.3.4. Сравнение теорий активных столкновений и переходного состояния
При реакции между двумя атомами А и В константа равновесия при образовании активированного комплекса АВ#равна:
![]() . (21.55)
. (21.55)
Статистические суммы по состояниям атомов с массой mi, которые имеют три степени свободы поступательного движения, равны:
![]() ,
,![]() . (21.56)
. (21.56)
Активированный комплекс, образованный из двух атомов, кроме трех поступательных, имеет две вращательные степени свободы и для него
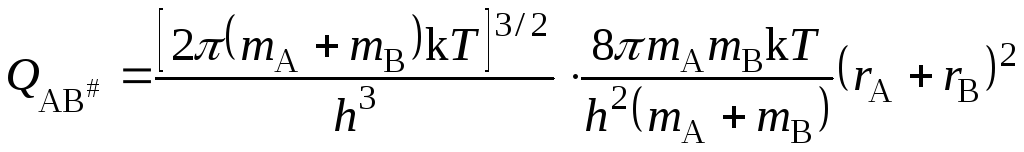 . (21.57)
. (21.57)
Тогда по уравнению (21.45) константа скорости будет равна (если положить = 1):
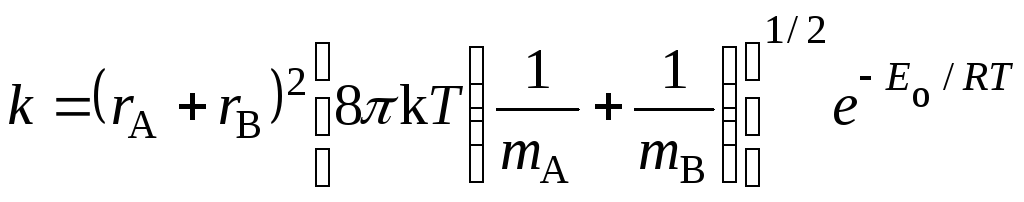 , (21.58)
, (21.58)
что совпадает с уравнением теории активных соударений (21.8).
При реакции между многоатомными молекулами, которые имеют поступательные, вращательные и колебательные степени свободы со статистической суммой по состояниям qiна одну степень свободы, теория активированного комплекса дает в уравнении (21.58) дополнительный множитель (qкол/qвращ)5, который аналогичен стерическому фактору теории соударений и называется иногда вероятностным фактором.
21.4. Реакции в растворах
Р
12
Первые систематические исследования влияния растворителя на скорость реакций были проведены в конце ХIХ века Н.А.Меншуткиным. Он открыл новый класс реакций образования четвертичных аммониевых солей из алкилгалогенидов RГ и третичных аминов R3N:
RГ + R3NR NГ
Особенностью этих реакций является их чрезвычайно малая скорость, чему соответствует малое значение предэкспоненциальных множителей Aв уравнении Аррениуса – величиныAимеют порядок 102–104вместо "нормального" значения 3.1011л.моль-1.с-1, а значения стерического множителяPимеют порядок 10-8– 10-10. В таблице 21.1 приведены кинетические характеристики для некоторых из этих реакций.
Предложены различные объяснения малой скорости реакций Меншуткина. Одной из причин может быть необходимость определенной ориентации молекул в момент столкновения; кроме того, реакция может проходить при столкновении активированных молекул, в которых осуществляется подходящее распределение энергии по внутренним степеням свободы, например, когда один из колеблющихся атомов наиболее отклонился от нормального положения. Различная сольватация растворителем исходных веществ и активированного комплекса влияет на энергию активации, что также сказывается на константе скорости.
Таблица21.1
Кинетические характеристики некоторых реакций Меншуткина
|
Реакция |
Растворитель |
A л.моль-1с-1 |
E кДж/моль |
P |
|
(C2H5)3N + C2H5Br |
C6H6 CH3COCH3 |
2,8.102 8,5.103 |
42,8 49,0 |
5,3.10–10 1,6.10–8 |
|
C6H5(CH3)2N + CH3I |
C6H5NO2 C2H2Cl4 |
2,6.104 2,1.104 |
54,5 48,9 |
5,3.10–8 4,8.10–8 |
|
C6H5(CH3)2N + C2H5 |
CH3COCH3 |
2,7.104 |
57,2 |
6,3.10–8 |
С другой стороны, можно привести некоторые примеры реакций, скорости которых мало отличаются в газовой фазе и растворе. В таблице 21.2 приведены относительные константы скорости и энергии активации реакции распада оксида азота N2O5в различных растворителях.
Некоторые важные выводы о кинетике реакций в растворах можно получить, используя теорию активированного комплекса.
Для реакции
А + В АВ#продукты
константа скорости равна
![]() . (21.59)
. (21.59)
Если реакция протекает при достаточно
низких давлениях в газовой![]() фазе и разбавленных растворах , то
фазе и разбавленных растворах , то
![]()
![]() , (21.60)
, (21.60)
откуда отношение констант скоростей будет равно
![]() . (21.61)
. (21.61)
Таблица 21.2
Кинетические характеристики реакции распада N2O5
|
Растворитель |
|
E кДж/моль |
|
Газовая фаза |
1,00 |
102,5 |
|
CH3NO2 |
0,81 |
102,5 |
|
Br2 |
1,14 |
100,4 |
|
CHCl2CCl3 |
1,16 |
104,6 |
|
CCl4 |
1,24 |
100,8 |
|
CH2ClCH2Cl |
1,26 |
102,1 |
|
CHCl3 |
1,45 |
102,9 |
Константа равновесия образования активированного комплекса выражается через концентрации c реагирующих веществ:
![]() . (21.62)
. (21.62)
Для газов
![]() ,
,![]() гдеpi– парциальное
давлениеi-го компонента в газовой
фазе. По закону Рауляpi
= poixi, а для разбавленных растворов выполняется
примерное равенство
гдеpi– парциальное
давлениеi-го компонента в газовой
фазе. По закону Рауляpi
= poixi, а для разбавленных растворов выполняется
примерное равенство![]() ,
гдеVo– молярный объем
чистого растворителя; таким образом
,
гдеVo– молярный объем
чистого растворителя; таким образом
 . (21.63)
. (21.63)
Подставляя концентрации веществ А, В, АВ#в уравнение (21.62), а затем в (21.61), получим для реакцииn-го порядка
 . (21.64)
. (21.64)
Это уравнение получено Бенсоном. Если предположить, что молярные объемы растворителя и растворенных веществ примерно равны, молярный объем АВ#равен сумме молярных объемов А и В, а также ввести некоторые дополнительные упрощения, то получим соотношение
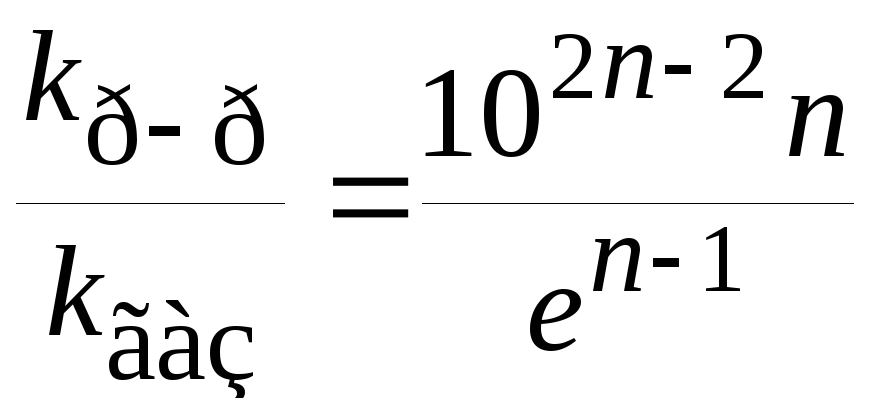 . (21.65)
. (21.65)
Это означает, что для реакций первого порядка (n= 1) константы скорости реакции в газовой фазе и растворе должны быть одинаковы, если механизм и энергии активации в двух фазах не отличаются. Для бимолекулярной реакцииkp-p/kгаз75, т.е. реакция в растворе должна протекать быстрее, чем в газовой фазе.
В случае неидеальных растворов константа равновесия должна выражаться не через концентрации, а через активности ai = cifi(fi– коэффициент активности):
![]() . (21.66)
. (21.66)
Подставляя значение K#в уравнение (21.45), получим
![]() . (21.67)
. (21.67)
Уравнение (21.67), полученное Бренстедом (1922) и Бьеррумом (1924), позволяет объяснить влияние на скорость таких факторов как диэлектрическая проницаемость среды, заряд реагирующих частиц, концентрация добавляемых электролитов и т.п.
Если реагируют нейтральные частицы, то для определения коэффициентов активности можно воспользоваться уравнением Ленгмюра:
![]() , (21.68)
, (21.68)
где – постоянная,H– теплота испарения веществ. В этом случае
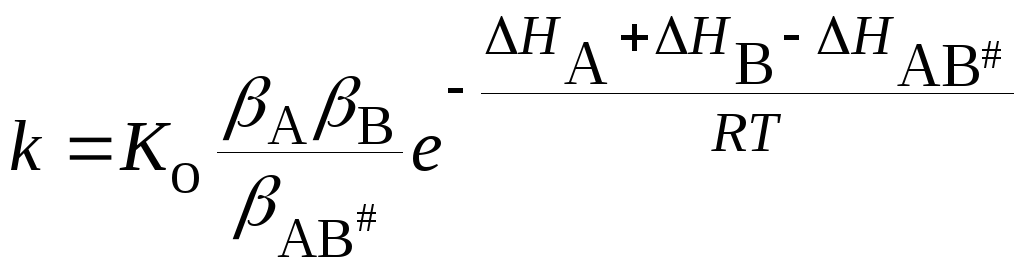 . (21.69)
. (21.69)
Если в растворе нет сильного межмолекулярного
взаимодействия между растворителем и
реагирующими веществами А, В, АВ#,
то показатель степени мало отличается
при протекании реакции в газовой фазе
и в растворе, а изменение константы
скорости будет определяться
предэкспоненциальным множителем,
зависящим отA,B,![]() .
Взаимодействие растворителя с реагентами
– сольватация – приводит к увеличению
или уменьшению скорости реакции.
.
Взаимодействие растворителя с реагентами
– сольватация – приводит к увеличению
или уменьшению скорости реакции.
При реакциях между ионами проявляется сильное электростатическое взаимодействие, зависящее от диэлектрической проницаемости среды . Для оценки влиянияна кинетику ионных реакций используем уравнение теории активированного комплекса:
![]() (21.70)
(21.70)
и представим энергию активации G#в виде двух составляющих, которые соответствуют неэлектростатическому и электростатическому взаимодействиям:
![]() . (21.71)
. (21.71)
Изменение энергии Гиббса при переносе
иона из вакуума в среду с диэлектрической
проницаемостью можно представить по Борну (см. разд.
15.2) как сумму слагаемых: 1) изменение
энергии при разряде иона в вакууме,
равное -ziei/2ri(ziиri– заряд
и радиус иона); 2) изменение энергии при
переносе незаряженной частицы в
бесконечно разбавленный раствор; 3)
изменение энергии при заряжении иона,
равноеzi2ei2/2ri.
Второе слагаемое можно включить в
неэлектростатическую составляющую![]() ,
а изменение энергии при электростатическом
взаимодействии будет равно в расчете
на один моль
,
а изменение энергии при электростатическом
взаимодействии будет равно в расчете
на один моль
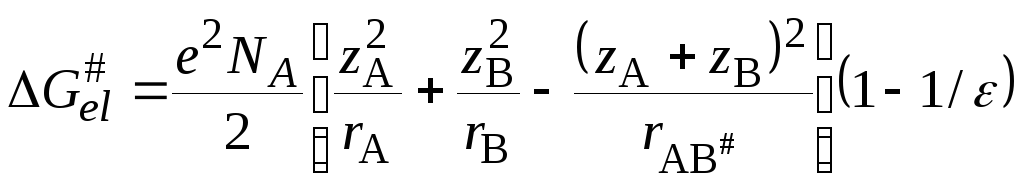 . (21.72)
. (21.72)
Подстановка уравнения (21.71) в (21.70) и логарифмирование дает
![]() . (21.73)
. (21.73)
Обозначив первые два члена справа как
lnkoи подставив значения![]() из
уравнения (21.72), получим:
из
уравнения (21.72), получим:
 . (21.74)
. (21.74)
Рис. 21.7. Зависимость
lnk
от обратной диэлектрической
проницаемости растворителя

При реакции между ионами коэффициенты активности в уравнении (21.67) можно представить на основании теории растворов сильных электролитов Дебая – Гюккеля (раздел 15.5):
![]() . (21.75)
. (21.75)
Представив уравнение (21.67) в логарифмической
форме и выразив коэффициенты активности
по уравнению Дебая – Гюккеля (заряд
активированного комплекса
![]() =zA+zB), получим для
логарифма константы скорости ионной
реакции:
=zA+zB), получим для
логарифма константы скорости ионной
реакции:
![]() . (21.76)
. (21.76)
Для очень разбавленных растворов с
малой ионной силой можно использовать
первое приближение теории Дебая –
Гюккеля
![]() ,
в этом случае
,
в этом случае
![]() , (21.77)
, (21.77)
т.е. логарифм константы скорости является линейной функцией от корня из ионной силы.
Влияние ионной силы на константу скорости реакции вследствие изменения активности реагентов называется первичным солевым эффектом. Скорость реакции может меняться также за счет уменьшения эффективной концентрации ионного реагента, образующегося при диссоциации слабого электролита, при добавках соли. Этовторичный солевой эффект. Например, каталитическое действие уксусной кислоты на инверсию сахарозы уменьшается в присутствии ацетатов щелочных металлов, так как в этом случае сильно понижается эффективная концентрация ионов водорода.
Совокупность явлений, связанных с солевым эффектом, показывает, что изменение среды, в которой протекает реакция, влияет на ее скорость так же, как и на равновесие между реагентами. И для констант скоростей и для констант равновесий выполняется один и тот же предельный закон, а отклонения от него, связанные со специфическими взаимодействиями, проявляются в одних и тех же условиях и имеют одинаковый характер. Аналогичное влияние на скорость и равновесие подтверждает справедливость общей теории переходного состояния. Существование солевого эффекта показывает, что влияние свойств среды на скорость реакции определяется разностью стандартных потенциалов реагирующих веществ и активированного комплекса, причем влияние на активированный комплекс в принципе не отличается от влияния на стабильную молекулу.
В связи с этим было предложено ряд корреляционных уравнений, основанных на так называемом принципе линейных соотношений свободной энергии. Согласно этому принципу, если молекулу представить как совокупность реагирующей группы X и нереагирующего остатка R, между которыми отсутствуют сильные специфические взаимодействия, то:
1) для любой реакции, затрагивающей X, изменение G#, вызываемые изменениями в R, линейно связаны с изменениямиGoв той же реакции;
2) изменения G#илиGo, вызываемые изменениями в R, для одной реакции с участием группы X1, линейно связаны с соответствующими величинами для другой реакции с участием X1и для реакции с участием другой группы X2.
Принцип линейной зависимости свободных энергий можно представить уравнениями:
![]() , (21.78)
, (21.78)
![]() , (21.79)
, (21.79)
где R–
оператор Леффлера – Грюнвальда,
отражающий влияние изменения строения
на какую-либо зависящую от него величину:![]() и
и![]() относятся к реакции 1, а
относятся к реакции 1, а![]() и
и![]() – к реакции 2. Величиныa1,a2,
b12не зависят от R, но зависят
от рассматриваемых реакций.
– к реакции 2. Величиныa1,a2,
b12не зависят от R, но зависят
от рассматриваемых реакций.
Наиболее изученной областью применения уравнения (21.78) является зависимость, полученная Бренстедом, для скорости реакций, катализируемых кислотами или основаниями:
Rlgk=RlgK. (21.80)
Она связывает константу скорости k данной каталитической реакции, катализируемой рядом кислот или оснований, с константами равновесияK, характеризующими силу кислоты или основания. Параметрхарактеризует каталитическую реакцию и не зависит от катализатора.
Гаммет предложил уравнение, которое учитывает влияние заместителя на константу скорости или равновесия в какой-либо реакции, характерной для данного класса ароматических соединений. Уравнение Гамметазаписывается в виде
lgk= lgko+, (21.81)
где kиko– константы скорости реакции замещенного и незамещенного ароматического соединения рассматриваемого класса,- константа, характеризующая заместитель,- реакционная константа, зависящая от реакции, среды и температуры.
Так как из экспериментальных данных можно получить лишь величину произведения , то необходимо приписать некоторое исходное значение каким-либои. Гаммет принял= 1 для равновесия ионизации замещенных бензойных кислот. Тогда заместительiможно характеризовать константой, определяемой из соотношения
= lgki– lgko, (21.82)
где ko– константа ионизации бензойной кислоты, аki– константа ионизации замещенной бензойной кислоты. Беря эти значения, можно получить величинудля других реакций, а из этого, в свою очередь, могут быть вычисленыдля заместителей, эффект которых на силу бензойных кислот ранее не был определен.
Уравнение Гаммета мало применимо к алифатическим соединениям, а также к реакциям с участием молекул с заместителями в орто-положении, когда возникают стерические затруднения.
