Глава 14. Элементы статистической термодинамики

14.1. Основные понятия. Расчет вероятности

Статистическая термодинамика устанавливает связь между макроскопическими свойствами системы и свойствами образующих систему частиц, основываясь на законах механики и теории вероятностей. Статистическая термодинамика рассматривает механику большого числа частиц. Механические переменные выступают как случайные величины с определенными вероятностями появления. Термодинамические величины рассматриваются либо как средние значения случайных величин (например, внутренняя энергия системы, находящейся в тепловом контакте с окружением), либо как характеристики распределения вероятностей (температура, энтропия, химический потенциал). Статистическая термодинамика объясняет все положения классической термодинамики, а также дает возможность разрабатывать методы расчета термодинамических функций и констант равновесия на основе получаемых опытным путем молекулярных характеристик.

Все молекулы, составляющие какую-либо систему, отличаются друг от друга своим положением в пространстве, т.е. значениями координат, а также скоростями движения и энергиями. Если считать, что эти величины могут меняться непрерывно, то любому макросостоянию будет соответствовать бесконечно большое число микросостояний.

Как уже отмечалось в разделе 3.8, для описания положения частицы используется понятие фазового пространства – воображаемого многомерного пространства, координатами которого являются декартовы координаты атомов и проекции импульса (р=mv) на трехмерные координатные оси. Для одноатомной молекулы фазовое пространство имеет шесть координат – три координаты положенияx,y,zи три проекции импульса на координатные осир_х,р_у,р_z. Дляn-атомной молекулы требуется 6nвеличин, а фазовое пространство в этом случае будет 6n-мерным.

Каждая молекула системы изображается точкой фазового пространства, а микросостояние системы характеризуется набором таких точек.

Фазовое пространство разбивается на отдельные ячейки – столь малые области, чтобы изменение координат в пределах одной области не могло изменить данного микросостояния. Подсчет числа микросостояний, т.е. термодинамической вероятности состояния, в этом случае сводится к нахождению числа возможных способов размещения всех молекул по различным ячейкам фазового пространства.

Конкретное вычисление термодинамической вероятности зависит от дальнейших допущений об областях и частицах. По классической статистике Больцмана размер областей неопределенен, частицы различимы (их можно пронумеровать), а их энергетический спектр непрерывен. В квантовых статистиках учитывается, что возможные состояния системы могут быть только дискретными, и на способы распределения влияет спиновое число частиц. Для тождественных частиц с полуцелым спином (фермионов) выполняется запрет Паули: в заданном квантовом одночастичном состоянии может находиться не более одной частицы. Для частиц с нулевым или целым спином (бозонов) ограничения на способы заполнения состояний отсутствуют. Различия фермионов и бозонов приводят к тому, что ансамбли этих частиц подчиняются разным статистикам: Ферми –Дирака (для фермионов) и Бозе – Эйнштейна (для бозонов). Однако, вдали от абсолютного нулямолекулярные системыведут себя практически одинаково, независимо от того, составлены они из бозонов или фермионов, а их особенности не проявляются в распределении. В таких случаях при подсчете квантовых состояний формально допустимо описывать систему как образованную пронумерованными частицами, рассматривать способы распределения частиц по ячейкам фазового пространства как для классических частиц по статистике Больцмана, но вводить поправку на неразличимость тождественных частиц с помощью множителя 1/N!. Тогда термодинамическая вероятность состояния системы, состоящей изNчастиц, равна

W=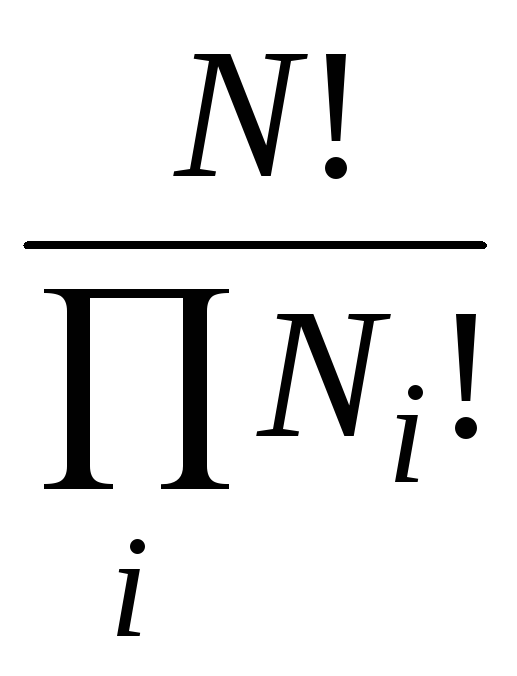, (14.1)