Практическое вычисление определителей

При конкретном вычислении определителей широко используются формулы разложения определителей по строке или столбцу, а также свойство 7, позволяющее, не изменяя величины определителя, прибавлять к любой его строке (или столбцу) произвольную линейную комбинацию других его строк (столбцов). Особенно удобно использовать формулу разложения по тем строкам (или столбцам), многие элементы которых равны нулю. Рассмотрим конкретный пример.

Задача 1.2.Вычислить определитель пятого порядка.

Во второй строке есть два элемента с нулевыми координатами, в связи с чем можно раскрывать определитель по элементам второй строки. Однако для уменьшения объема последующих вычислений можно добиться наибольшего числа нулей во второй строке. Прибавляя к элементам третьего столбца соответствующие элементы второго столбца, получим:

Затем, прибавляя к элементам второго столбца соответствующие удвоенные значения четвертого столбца, будем иметь:

Далее разложим определитель по элементам второй строки. В результате получим:

.

Теперь в определителе четвертого порядка добьемся наибольшего числа нулей в третьей строке. Для этого умножим на элементы первой строки и сложим их с соответствующими элементами третьей строки.

.

Разложим определитель четвертого порядка по элементам третьей строки

.

В определителе третьего порядка добьемся наибольшего числа нулей во втором столбце. Для этого элементы первой строки умножим на и сложим с соответствующими элементами третьей строки.

.

Здесь можно разложить определитель третьего порядка по элементам второго столбца. При этом, получим:

.

Наконец, вычисляя определитель второго порядка, будем иметь:

Тема 1.3. Обратная матрица. Ранг матрицы Обратная матрица

Одно из важнейших свойств умножения чисел состоит в том, что для каждого числа , отличного от нуля, существует обратноетакое, что

.

Оказывается, что нечто подобное имеет место и для матриц, причем роль условия играет условие, состоящее в том, что определитель матрицыне равен нулю.

Определение 1.11.Квадратная матрица называется невырожденной, если ее определитель не равен нулюи вырожденной, если ее определитель обращается в нуль

Определение 1.12.Матрицаназывается обратной по отношению к матрице, если имеет место равенство:

.

Условие существования обратной матрицы сформулируем в виде следующей теоремы:

Теорема 1.1.Для того, чтобы квадратная матрицаимела обратную, необходимо и достаточно, чтобы она была невырожденной.

Обратная матрица вычисляется по следующим правилам:

1. Вычисляется определитель исходной (10.2) квадратной матрицы-го порядка.

2. Формируется матрица, составленная из алгебраических дополнений элементов исходной квадратной матрицы. Такая матрица называется союзной по отношению к матрицеи обозначается.

Таким образом, на этом этапе имеем:

.

3. Транспонируют союзную матрицу, тем самым определяя так называемую присоединенную матрицу матрицы . Такая матрица обозначаетсяи представляется следующим образом:

.

4. Вычисляется обратная матрица по отношению к матрице.

.

Задача 1.3.Дана матрица. Найти обратную по отношению к заданной.

Вычислим определитель матрицы .

.

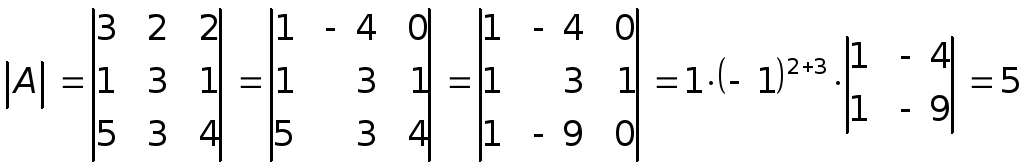Находим алгебраические дополнения элементов определителя.

;;;

;;;

;;.

Затем формируем союзную матрицу по отношению к матрице :

.

Определим присоединенную матрицу по отношению к матрице :

.

Вычисляем обратную матрицу по отношению к матрице:

.