Тема 2.2. Прямая на плоскости

Д ве взаимно перпендикулярные прямые, на каждой из ко­то­рых указано положительное направление и масштаб, образуют прямоугольную декартову систему координат (рис: 2.6). :

Рис. 2.6

Точка называется началом координат, ось - осью абсцисс, ось -осью ординат. Положение на плоскости любой точки определяется двумя числами (координатами): (рис.2.6).

Теорема 2.9 Расстояние между точками и (рис.2.7) измеряется по формуле

Рис. 2.7

Теорема 2.10 Если точка делит отрезок в отношении ( называется коэффициентом пропорциональности), то ее координаты находят так;

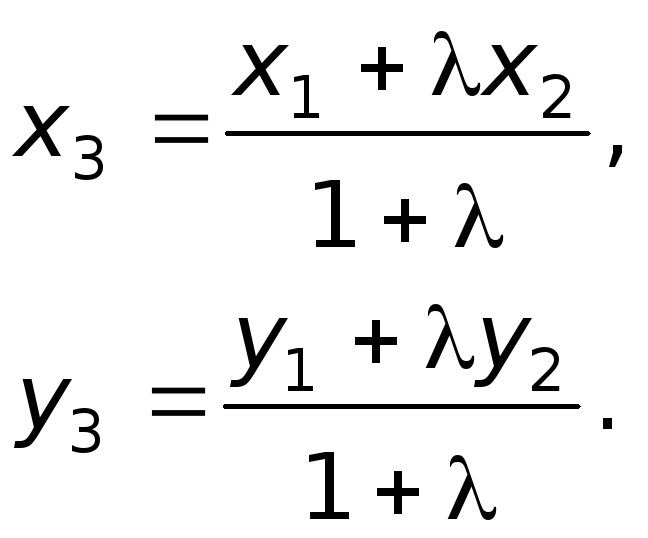
Следствие В частном случае, когда отрезок делится пополам, , получим так называемые формулы половинного деления;

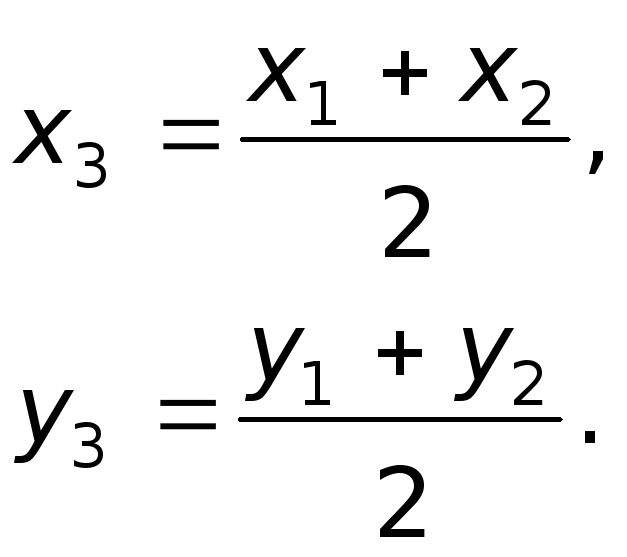
Теорема 2.11 Площадь треугольника с известными вершинами равна;

В декартовом базисе прямая изображается уравнением первой степени с двумя неизвестными и

Рассмотрим различные формы задания уравнения прямой на плоскости.

Теорема 2.12 В прямоугольной системе координат любая прямая задается уравнением первой степени, называемым общим уравнением прямой

,

где - постоянные коэффициенты, причем .

Уравнение прямой с угловым коэффициентом:

З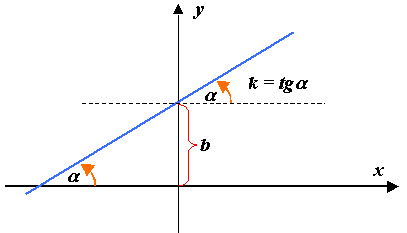 десь параметры и имеют определенный геометрический смысл (рис2.8).

Рис. 2.8

и называется угловым коэффициентом.

- угол, образованный прямой с положительным направ­ле­нием . В качестве положительного направления изме­ре­ния угла а принято направление против хода часовой стрелки (рис. 2.8).

– отрезок, отсекаемый прямой на оси ординат.

Выполнив несложные алгебраические преобразования, можно от общего уравнения прямой перейти к уравнению пря­мой с угловым коэффициентом. При этом

,

Уравнение прямой в отрезках выглядит так:

.

Здесь и - отрезки, отсекаемые прямой на осях абсцисс и ординат соответственно. Их связь с коэффициентами общего уравнения

,

.

В этой форме можно представить уравнение прямой, не проходящей через начало координат, т.е. если .

Нормальное уравнение прямой:

Геометрический смысл коэффициентов этого уравнения:

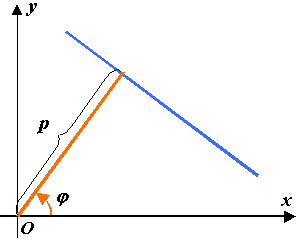- длина перпендикуляра, опущенного из начала координат на прямую; - угол, образованный этим перпендикуляром, с положительным направлением оси (рис.2.9).

Рис. 2.9

Чтобы перейти к этому виду уравнения прямой, надо умножить все члены общего уравнения на нормирующий множитель

.

Знак выбирается таким образом, чтобы

Уравнение пучка прямых описывает множество прямых, проходящих через точку с известными координатами:

.

Уравнение прямой, проходящей через две точки и :

Угол между прямыми в зависимости от формы задания уравнений прямых может быть найден по формуле:

или

.

З десь угол измеряется от прямой с угловым коэффици­ен­том или до прямой с параметрами или (рис.2.10):

Рис. 2.10

Из этих формул легко выводятся условия параллельности:

или

и перпендикулярности прямых:

или .

Координаты точки пересечения двух прямых опреде­ляют­ся как решение системы, составленной из уравнений прямых.

Теорема 2.13 Расстояние от точки до прямой (или ) определяется по формулам:

или

Задача 2.5 Дано общее уравнение прямой .

Написать: а) уравнение с угловым коэффициентом; б) уравнение в отрезках; в) нормальное уравнение. Построить прямую.

Решение

а) Оставим член с слева, а остальные перенесем в правую часть уравнения. Затем разделим обе части на коэффициент при , т.е. на -3. В результате получим уравнение с угловым коэффициентом

Задача 2.6 Написать уравнение прямой, проходящей через точку и отсекающей от координатного угла треугольник, площадью равной 3.

Решение

О чевидно, что таких прямых будет 2, а треугольники обра­зо­ваны во втором и четвертом квадрантах (рис.2.11):

Рис. 2.11

Запишем уравнение пучка прямых, проходящих через точку :

Преобразуем его к уравнению в отрезках:

.

Таким образом,

Так как и имеют разные знаки, то площадь указанных в условии задачи треугольников может быть найдена по формуле

Отсюда или

Решив квадратное уравнение, найдем

Тогда уравнения прямых будут иметь вид:

Задача 2.7 Дан треугольник с вершинами и . Написать уравнения сторон треугольника, медианы , высоты , найти длины медианы и высоты , угол при вершине , площадь треугольника .

Решение

П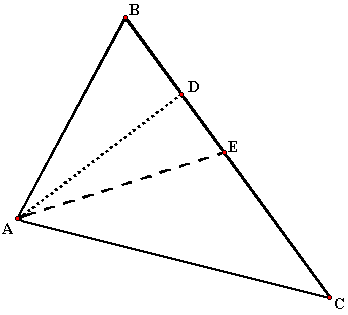 остроим треугольник с указанными вершинами и отметим все перечисленные элементы (рис. 2.12).

Рис. 2.12

Уравнения, сторон треугольника получим, используя уравнения прямой, проходящей через две точки.

Уравнение можно было записать и без таких выкладок, учитывая, что обе точки лежат на оси .

Для нахождения уравнения медианы предварительно определим координаты точки как середины отрезка :

Тогда уравнение медианы будет иметь вид

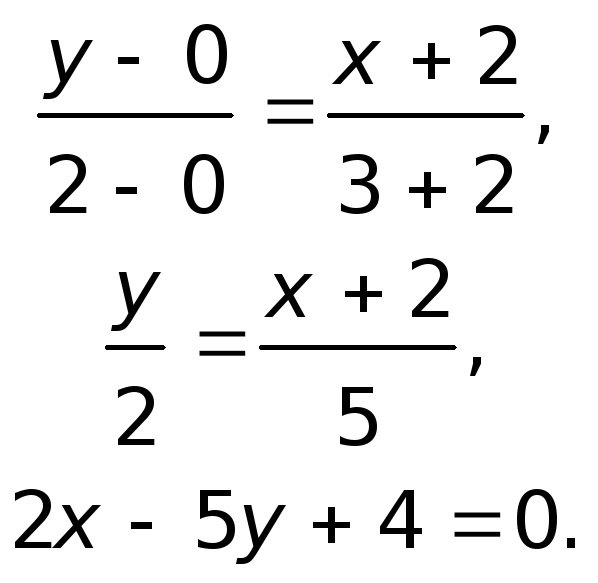
Длину определим как расстояние между точками и :

.

Запишем уравнение пучка прямых, проходящих через вершину :

Так как высота перпендикулярна стороне треугольника , то их угловые коэффициенты связаны так:

Из уравнения легко найти Тогда , и уравнение высоты будет

или

.

Длину высоты определим как расстояние от точки до прямой :

Так как мы установили общие уравнения прямых и , то воспользуемся соответствующей формулой для определения угла при вершине треугольника .

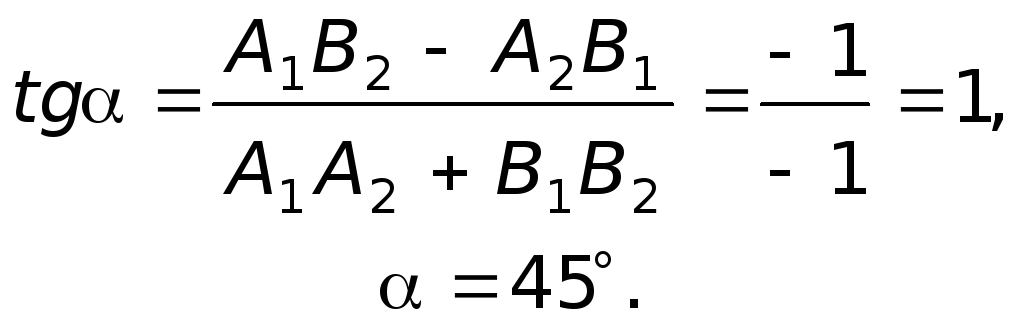
Площадь треугольника равна

.

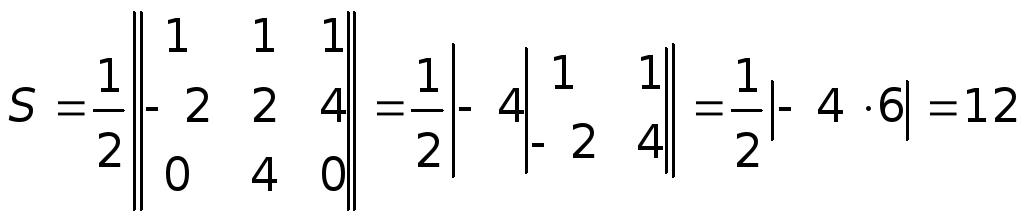Задача 2.8 Найти точку пересечения медиан и точку пересечения высот треугольника, вершины которого и .

Решение

С троим треугольник, показываем точки пересечения его медиан и высот (рис.2.13).

Рис.2.13

Определим координаты точки как середины отрезка , воспользовавшись формулами половинного деления

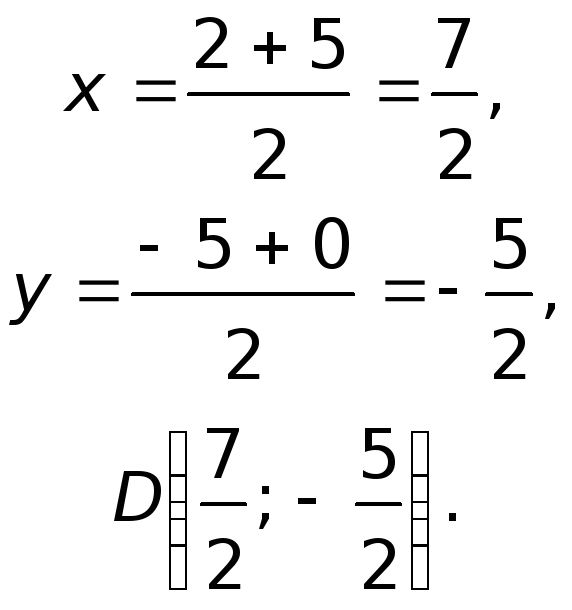
Для определения координат точки пересечения медиан воспользуемся свойством этой точки, согласно которому она делит медиану в отношении , считая от вершины, т.е. . Тогда для точки

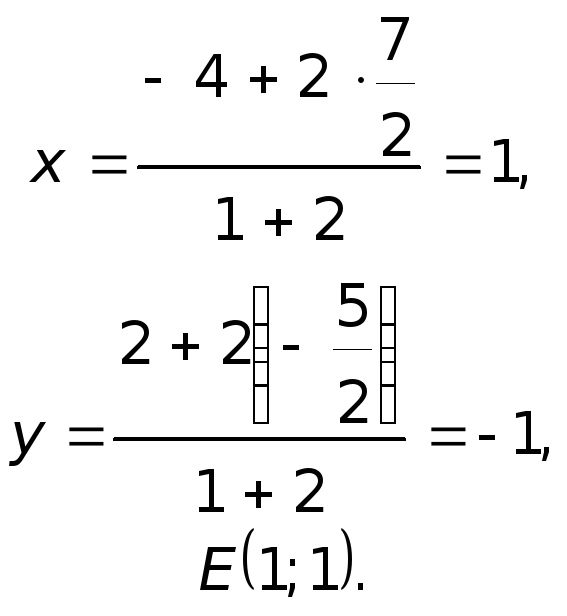
Треугольник является равнобедренным, так как длины сторон и равны:

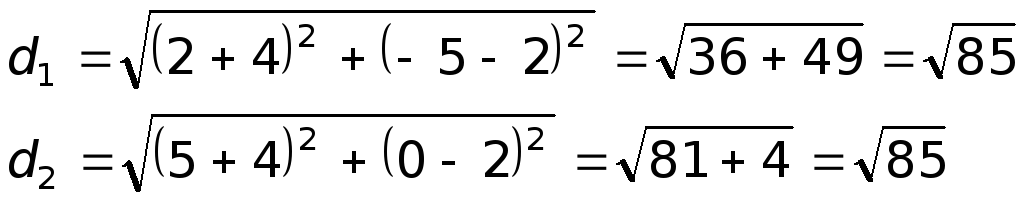
Следовательно, медиана будет и высотой. Отсюда уравнение высоты определим как уравнение прямой, проходящей через точки :

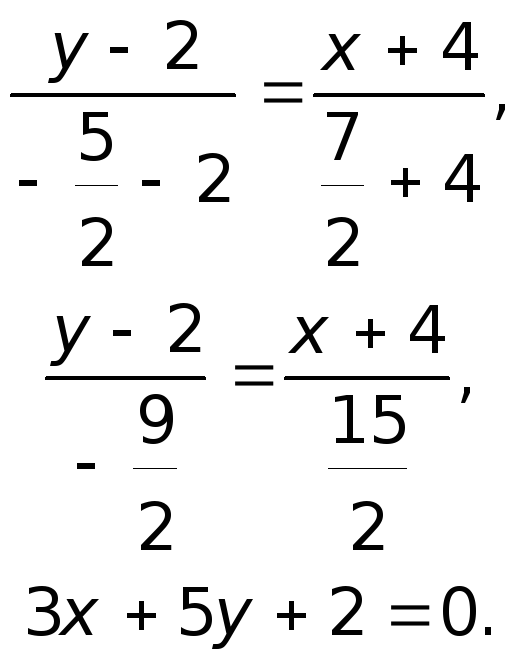
Уравнение пучка прямых, проходящих через точку может быть записано как

.

Уравнение находим через известные координаты концов отрезка:

Так как высота перпендикулярна , то ее угловой коэффициент и уравнение будет

или

Координаты точки пересечения высот и определим из решения системы, составленной из уравнений высот:

47