2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Тема 2.1. Элементы векторной алгебры

Векторы. Основные понятия и определения

В математике и ее приложениях встречаются различные величины. Некоторые из них (длина, площадь, объем, масса) полностью определяются числом. Такие величины называют скалярными. Для определения других величин одного числового значения недостаточно, необходимо еще указать и присущее им направление (к таким величинам относят силу, скорость, ускорение и т. д.). Такие величины называют векторными.

Определение 2.1. Отрезок прямой линии называют направленным отрезком или вектором, если указано, какой из его концов считают за начало, а какой за конец.

Графически векторы обозначают следующим образом:

Длину вектора обычно называют его модулем и обозначают , .

Определение 2.2. Векторы, лежащие на параллельных прямых, называются коллинеарными.

Определение 2.3. Векторы называются компланарными, если они после сведения к общему началу лежат в одной плоскости.

Проекция вектора на ось

Проекция вектора на ось употребляется в двух понятиях: геометрическом и алгебраическом.

Определение 2.4. Векторной проекцией вектора на ось называется вектор , где и соответственно проекции точек начала и конца вектора (рис. 2.1)

Р ис. 2.1

Определение 2.5. Скалярной проекцией вектора на ось называется длина вектора , взятая со знаком плюс (если направления вектора и оси совпадают) или минус (если направления вектора и оси противоположны). В соответствии с приведенным определением имеем:

.

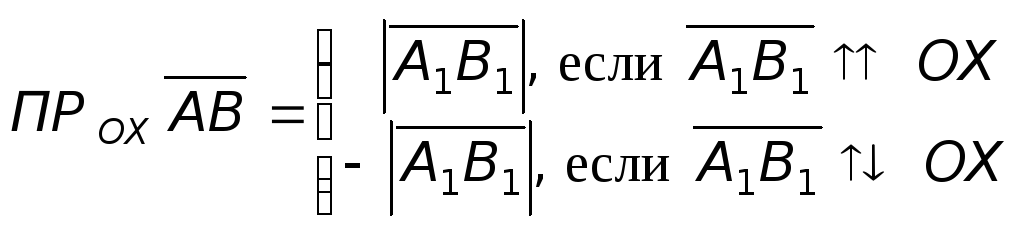Непосредственно процесс вычисления алгебраической проекции вектора на ось осуществляется путем применения теоремы 2.1.

Теорема 2.1. Проекция вектора на ось равна произведению модуля вектора на косинус угла между вектором и осью .

В соответствии с приведенной теоремой, имеем

.

Здесь - угол между вектором и осью .

Теорема 2.2. Проекция суммы векторов на ось равна сумме проекций слагаемых на ту же ось. В соответствии с теоремой имеем

.

Линейная зависимость векторов

Применяя линейные операции над векторами , можно составлять выражения вида:

,

которые называются линейными комбинациями векторов, где - числа, которые называются коэффициентами линейной комбинации.

Определение 2.6. Векторы называются линейно-зависимыми, тогда и только тогда, когда существуют действительные числа , не все равные нулю одновременно, для которых имеет место равенство:

Векторы называются линейно-независимыми, если их линейная комбинация превращается в нуль только при равенстве нулю всех коэффициентов линейной комбинации.

Заметим, что совокупность векторов называют системой векторов.

Условия линейной зависимости векторов представим в виде следующих теорем.

Теорема 2.3. Система векторов линейно-зависима тогда и только тогда, когда, по крайней мере, один из этих векторов можно представить в виде линейной комбинации остальных.

Теорема 2.4. Два вектора линейно - зависимы тогда и только тогда, когда они коллинеарны.

Теорема 2.5. Три вектора линейно - зависимы тогда и только тогда, когда они компланарны.

Векторный базис. Координаты вектора

Определение 2.8. Упорядоченная система линейно-независимых векторов векторного пространства называется его базисом, если любой вектор этого пространства можно представить в виде линейной комбинации векторов этой системы.

Число векторов, которые образуют базис, называется размерностью пространства.

Необходимо отметить, что имеют место следующие фундаментальные утверждения.

Утверждение 2.1. Любая упорядоченная тройка некомпла­нарных векторов образует базис в пространстве.

Утверждение 2.2. Любая упорядоченная пара неколлинеарных векторов , принадлежащих данной плоскости, образует базис на этой плоскости.

Непосредственно геометрическая интерпретация векторного базиса в пространстве представлена на рис. 2.2.

Здесь - векторы, образующие базис в пространстве.

Вектор - произвольный вектор пространства. При этом очевидно, что

.

Рис. 2.2.

Пусть - произвольный базис в пространстве. Тогда для любого вектора а существуют действительные числа такие, что выполняется равенство:

(2.1)

Равенство (2.1) принято называть разложением вектора по базису , а упорядоченную систему чисел - координатами вектора в этом базисе.

Теорема 2.6. Каждый вектор векторного пространства однозначно раскладывается по базису .

Следствие теоремы 2.6. Равные векторы имеют равные соот­вет­ствующие координаты в данном базисе, и, наоборот, если соответствующие координаты двух векторов в некотором базисе равны, то равны и сами векторы.

Арифметические операции над векторами, заданными своими координатами, можно выполнять в соответствии с теоремой 2.7.

Теорема 2.7. При сложении векторов их соответствующие координаты произвольном базисе складываются, а при умножении вектора на произвольное число , каждая компонента его координат множится на это число.

Таким образом, если векторы и представлены в некотором базисе

,

,

то в соответствии с теоремой 1.7

,

.

Аффинная система координат

Афинная система координат в пространстве определяется заданием базиса с общим началом в фиксированной точке , которая называется началом координат.

П

Рис. 2.3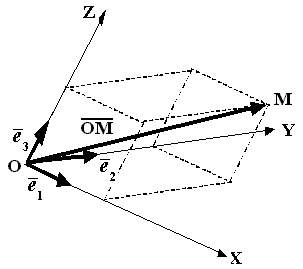

рямые, которые проходят через начало координат в направлении базисных векторов, называются осями координат. Оси, как правило, обозначают символами и называют соответственно осями абсцисс, ординат, аппликат. (Рис. 2.3).

Вектор , который соединяет начало координат с произвольной точкой , называется радиус-вектором точки .

Определение 2.9. Аффинными координатами точки называют координаты его радиус-вектора в данном базисе.

При этом записывают или .

Декартова прямоугольная система координат

Базис называют ортонормированным, если его векторы единичные и попарно-ортогональные.

С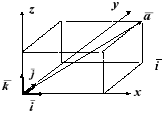 истема координат, базис которой ортонормированный, называется декартовой прямоугольной системой координат. Базисные векторы этой системы координат в пространстве обозначаются соответственно через .

Рис. 2.4

Разложение произвольного вектора а пространства по указанному базису имеет вид:

или , или .

В общем случае, прямоугольными координатами вектора называются алгебраические проекции вектора на оси координат.

Рассмотрим некоторые задачи.

Задача 2.1. Выяснить, будут ли векторы и линейно- зависимыми.

Решение.

Два вектора будут линейно-зависимыми тогда и только тогда, когда существуют и не равны нулю, для которых справедливо равенство:

Запишем последнее равенство в координатной форме

.

Выполняя операции умножения вектора на число и сложение векторов, получим:

.

Из последнего соотношения получают систему:

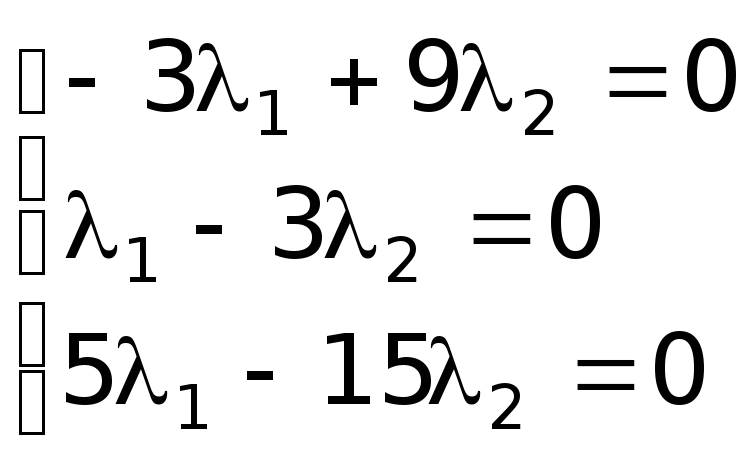
При этом, имеют ,

или

т.е.

Таким образом, векторы и линейно - зависимы.

Задача 2.2 Могут ли векторы , и образовывать базис?

Решение

Векторы и будут образовывать базис, если они линейно-независимы. При этом имеем:

,

при .

Представляя линейную комбинацию заданных векторов в координатной форме, получим:

,

Упрощая последнее выражение, придем к соотношению:

,

Для определения составим систему уравнений:

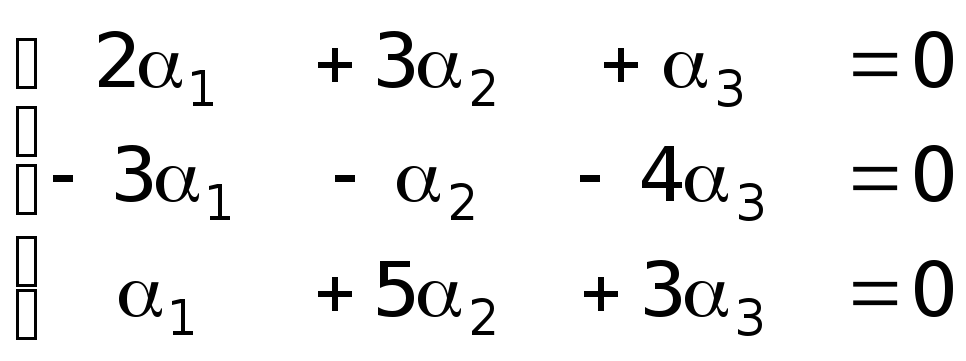
Определитель системы, составленный из коэффициентов при неизвестных, имеет вид:

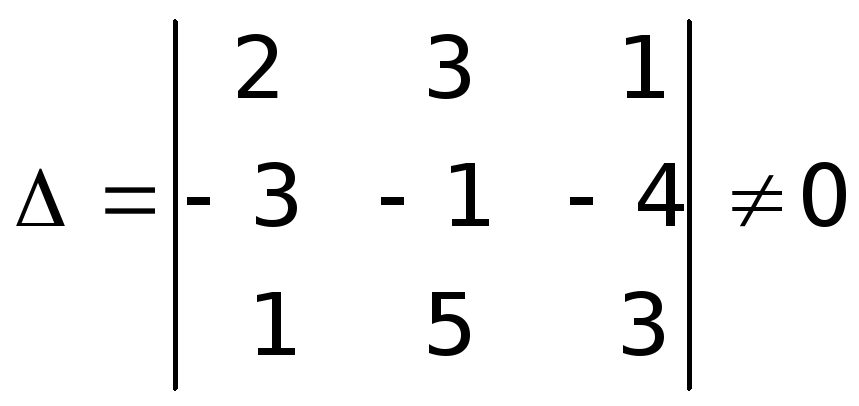
Следовательно, представленная однородная система уравнений имеет нулевое решение:

Таким образом, исходная система векторов линейно - независима, а значит, образует базис в пространстве. Причем этот базис будет афинным.

Задача 2.3. Векторы образуют базис в пространстве. Найти координаты вектора в базисе .

Решение.

Если векторы образуют базис в пространстве, то произвольный вектор можно разложить в базисе следующим образом:

.

При этом имеют

или

Приравнивая соответствующие координаты векторов, имеют:

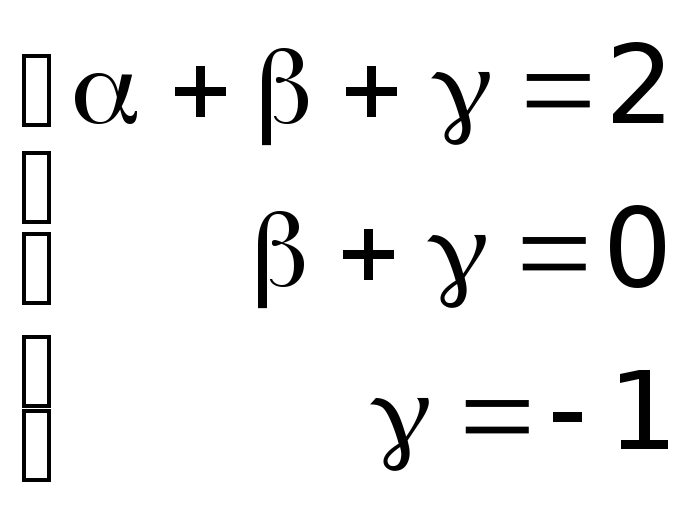
Решая представленную систему уравнений, получают

.

Таким образом, вектор в новом базисе имеет координаты: , a его разложение в базисе записывается в виде:

.

Выражение вектора через радиусы-векторы его начала н конца

Пусть в декартовой прямоугольной системе координат задан произвольный вектор . При этом, точки его начала и конца имеют следующие координаты и (рис. 2.5).

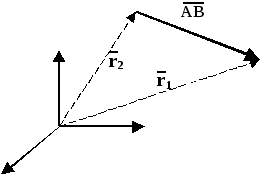
Рис. 2.5

Тогда или в координатной форме .

Вывод: Чтобы определить координаты вектора , необходимо из координат его конца вычесть соответствующие координаты его начала.

Скалярное произведение двух векторов

Определение 2.10. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Скалярное произведение векторов и обозначается или . Таким образом, в соответствии с определением, имеют

,

где - угол между векторами и .

Теорема 2.8. Если два вектора заданы своими декартовыми прямоугольными координатами

и

то скалярное произведение этих векторов равно сумме произведений их одноименных координат, т.е.

(2.2)

Некоторые приложения скалярного произведения

а) Вычисление модуля вектора

Если положить, что , то из соотношения (2.2) имеют

,

откуда определяют модуль вектора :

.

б) Вычисление угла между двумя векторами

Скалярным произведением двух векторов можно воспользоваться для вычисления угла между векторами:

Направляющие косинусы вектора

Обозначив через углы между вектором и , можно определить углы между заданным вектором и соответствующими осями координат. При этом, имеют:

.

Задача 2.4. Даны координаты вершин треугольника . Средствами векторной алгебры найти длину стороны , угол между сторонами и .

Решение.

а) Определим длину стороны . При этом найдем координаты вектора .

,

или

.

Далее имеем:

ед.

б) Определим угол между сторонами и .

Задача сводится к определению угла между векторами и .

.

Тогда

35