Тема 6.2. Определенный интеграл

Пусть функция определена на отрезке . Разделим этот отрезок на произвольных частей

Д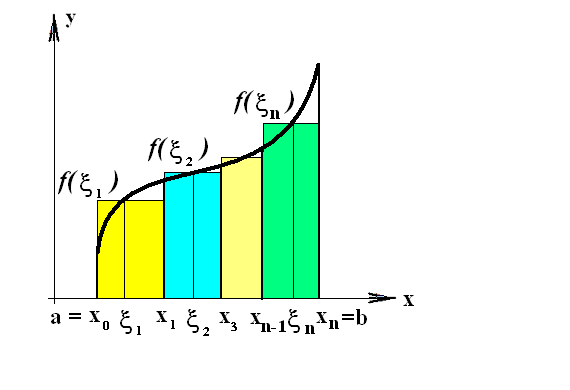ля каждого элементарного отрезка определим его длину и значение функции в произвольной точке (рис.6.1).

Рис. 6.1

Определение 6.3 Интегральной суммой от функции на отрезке называется сумма вида

Определение 6.4 Определенным интегралом функции на этом отрезке называется предел интегральной суммы: при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

Числа и называются соответственно нижним и: верхним пределами интегрирования.

Геометрический смысл определенного интеграла: это площадь криволинейной трапеции, т.е. фигуры, ограниченной линиями (рис.6.1):

Теорема 6.3 Достаточным условием существования определенного интервала на отрезке является непрерывность функции на этом отрезке.

Основные, свойства, определенного интеграла

где С - постоянная.

Для нахождения значения определенного интеграла используются формула Ньютона-Лейбница:

где - первообразная функции .

Формула интегрирования по частям для определенного интеграла выглядит так

При замене переменной

где новые значения пределов интегрирования и определяются из соотношений и , а функция , и ее производная непрерывны на .

Если - четная функция, то .

Если - нечетная функция, то .

.

Определенный интеграл используется для определения объема тела, образованного вращением дуги кривой вокруг оси OX

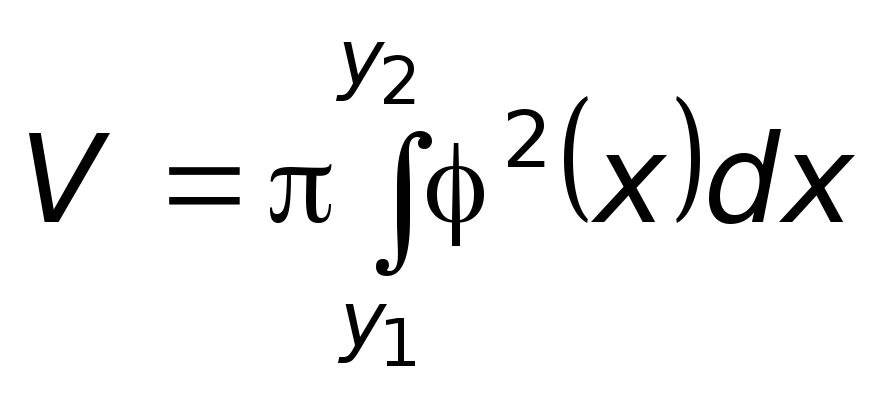
или кривой вокруг ОY

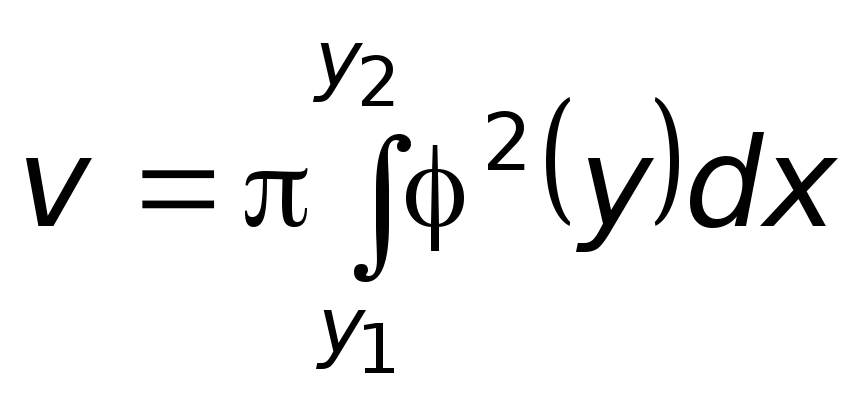
Задача 6.5 Вычислить:

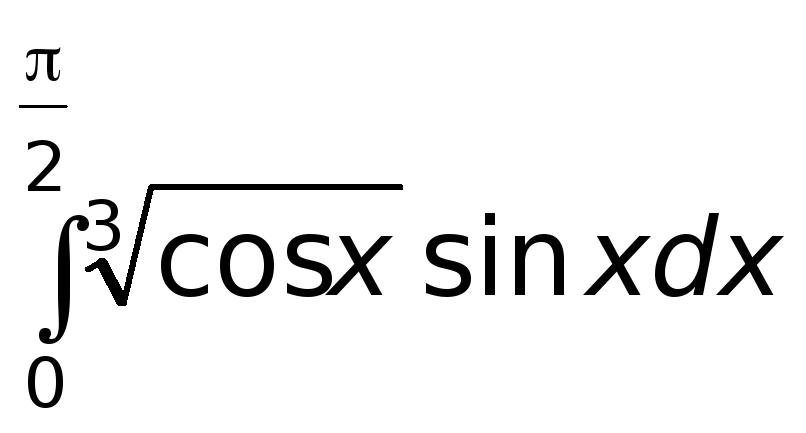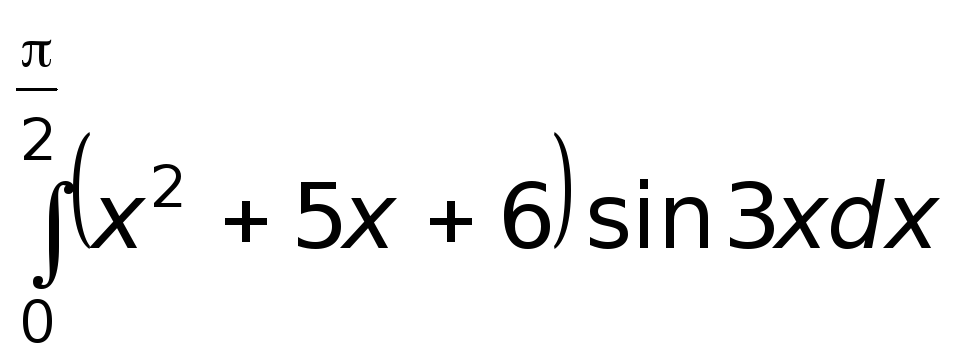а) , б) , в) .

Решение

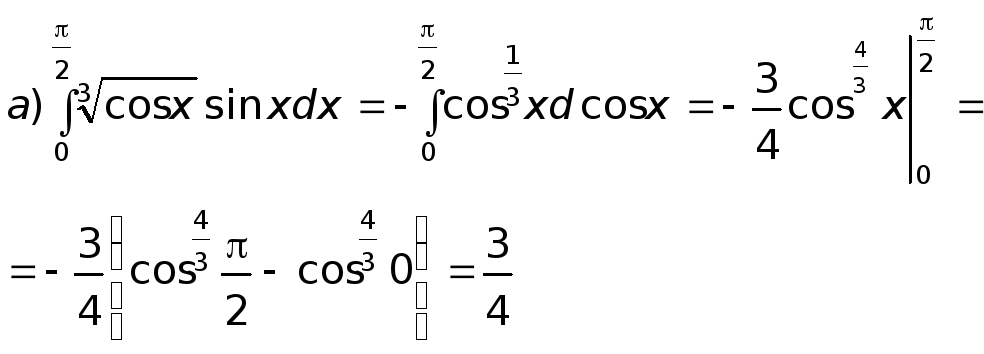
б) Интегрируем по частям:

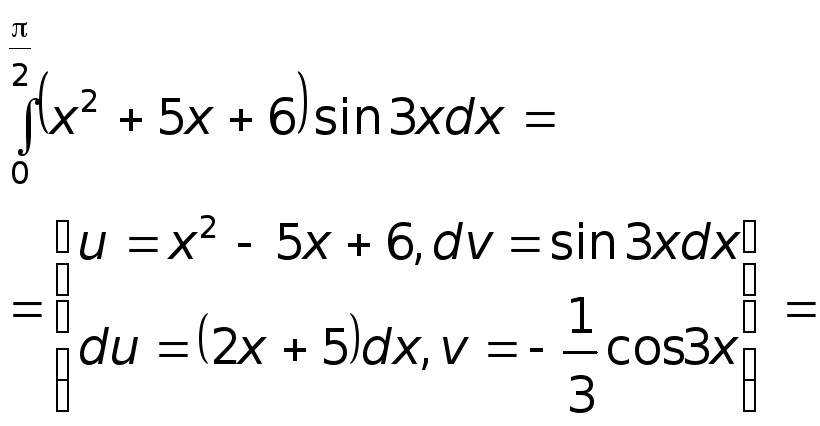
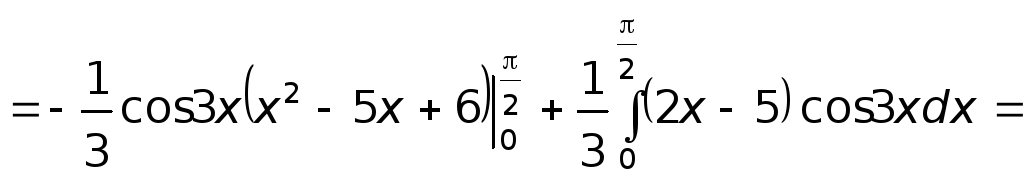
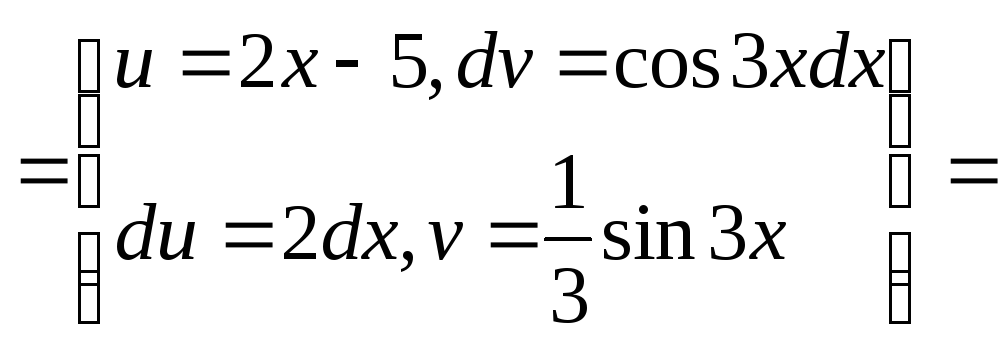
в)

Задача 6.6 Вычислить площадь, ограниченную линиями .

Решение

Для определения границ интегрирования решим систему

,

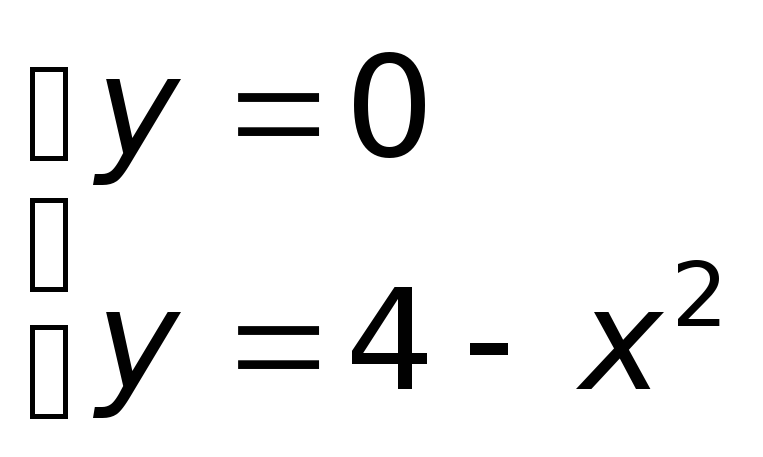откуда (рис.7.2).

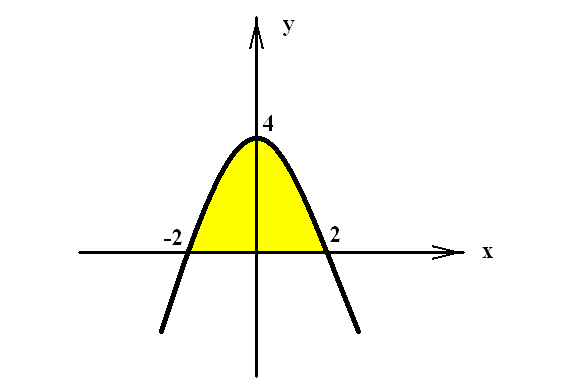
Рис. 7.2

Тогда

Задача 6.7 Определить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями и .

Решение

Из уравнения гиперболы определяем

Тогда объем тела, образованного вращением части гиперболы вокруг оси Оу в пределах от до равен

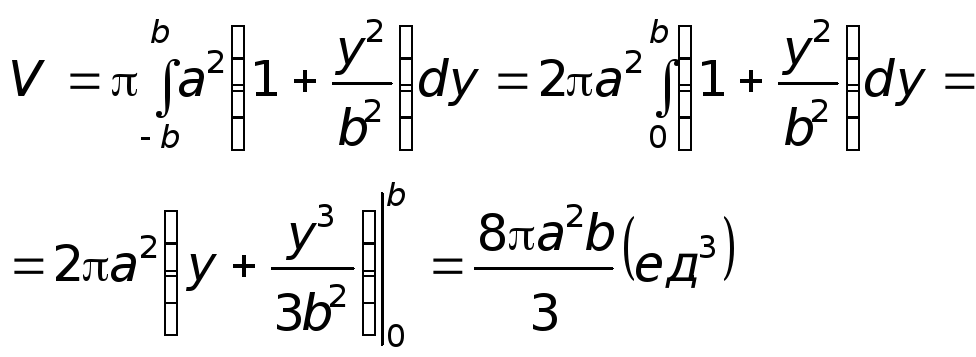
Тема 6.3. Несобственный интеграл

Определение 6.5 Интегралом с бесконечными пределами называется его предел, если последний существует и конечен:

,

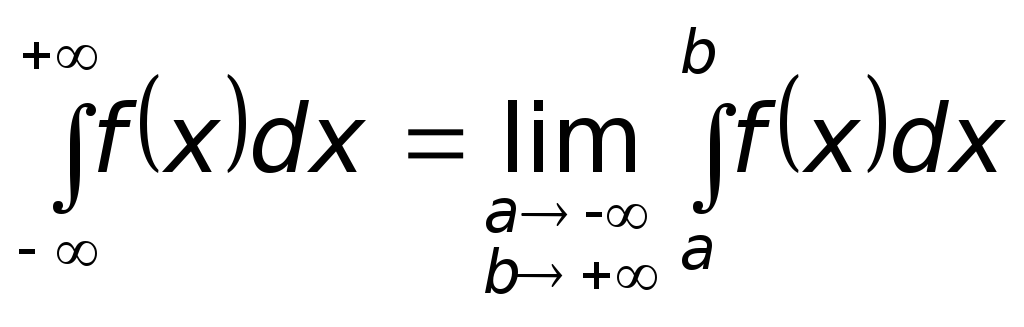
Определение 6.6. Если функция в точке имеет разрыв II рода и непрерывна во всех остальных точках этого отрезка, то

,

если эти пределы существуют и конечны.

Определение 6.7 Интегралы с бесконечными пределами и интегралы, от разрывных функций называются несобственными.

Определение 6.8 Если приведенные выше пределы конечны, то несобственные интегралы называются сходящимися, если это условие не выполняется - расходящимися.

Задача 6.8 Вычислить несобственный интеграл или показать, что он расходится

а) , б) , в) , г)

Решение

а)

б) интеграл расходится,

в) 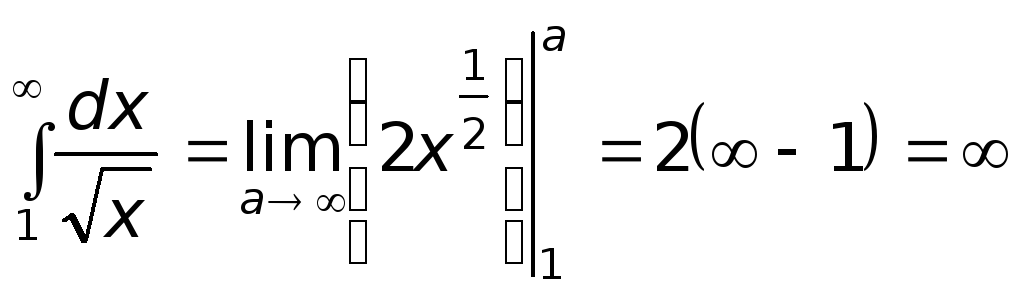- интеграл расходится

г)

Как показано в пунктах б) и в) при интеграл расходится. Если

.

106