Краткие сведения из математической статистики

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Случайной называют величину, которая в результате опыта может принять то или иное значение, заранее неизвестное. Случайная величина (СВ) может быть как дискретной так и непрерывной.

СВ полностью определена, если известно, с какой вероятностью p_i возможно появление каждого из принимаемых случайной величиной значений x_i.

В качестве меры вероятности p_j принимают относительную частоту (частость) появления конкретного значения x_i случайной величины

, ( 1 )

где n_j - количество появлений величины x_i в N опытах.

Закон распределения дискретной случайной величины Х, которая в результате опыта примет одно из х_j (j=1, 2, …, n) возможных значений, можно представить в виде таблицы.

x1	x2	x3	…	xn
p1	p2	p3	…	pn

Функция распределения дискретной случайной величины имеет вид

. ( 2 )

Когда переменная Х проходит через возможное значение x_j, функция F(х) меняется скачкообразно.

Для непрерывной случайной величины рассматривают вероятность, что ее значение не превысит Х<х, где х - некоторая текущая переменная. Ее функция распределения

. ( 3 )

Функция распределения всегда удовлетворяет условию

. ( 4 )

ПЛОТНОСТЬ ВЕРОЯТНОСТИ

Вероятность того, что случайная величина Х примет значение, находящееся внутри интервала (x, x+Dx) - это плотность вероятности.

. ( 5 )

Связь между функцией распределения и плотностью вероятности

. ( 6 )

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН

Точечные оценки.

Среднее арифметическое значение (математическое ожидание)

, ( 7 )

где N - число испытаний,

x_i- значения случайной величины, которые она принимала при этих испытаниях.

Характеристики разброса значений дискретной случайной величины

• дисперсия

; ( 8 )

• среднеквадратичное отклонение

; ( 9 )

• коэффициент вариации

. ( 10 )

Интервальные оценки.

При ограниченном количестве опытов пользуются доверительными интервалами для оценок случайной величины X. С доверительной вероятностью p истинное среднее значение лежит в интервале

. ( 11 )

Границы интервала определяются по критерию Пирсона (c²-тест) в зависимости от p и объема выборки N.

Для непрерывных случайных величин

• математическое ожидание (1-й момент выборки)

; ( 12 )

• дисперсия (2-й момент выборки)

. ( 13 )

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ПЛОТНОСТИ ВЕРОЯТНОСТИ

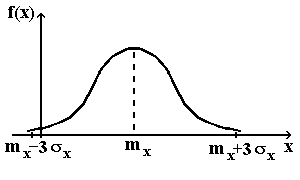
1. Нормальный закон распределения (закон Гаусса) (рис. 1) имеет плотность распределения

Рис. 1. Нормальный закон распределения

, ( 14 )

является одним из наиболее распространенных и часто применяемых на практике, например, при анализе ошибок измерений, точности обработки и в других случаях, когда отклонения x вызваны действием большого количества факторов, которые складываются.

2. Закон распределения Релея.

Рис. 2. Закон распределения Релея

Во многих прикладных задачах случайные величины могут принимать только положительные значения (амплитуды колебаний, потенциальная энергия упругой системы при случайных деформациях, кинетическая энергия системы при случайных скоростях и др.).

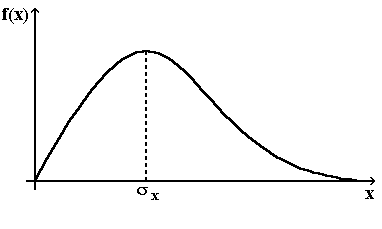
Случайные величины, при-нимающие только положительные значения, часто подчиняются функции распределения Релея

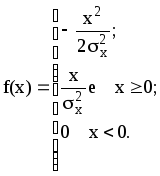( 15 )

Распределение Релея является однопараметрическим, т.е. зависит только от параметра s_x.

3. Закон распределения Пуассона.

Дискретную случайную величину Х называют распределенной по закону Пуассона, если ее возможные значения равны 0, 1, 2, ..., n, а вероятность того, что Х=n, выражается зависимостью

, ( 16 )

где а>0.

Математическое ожидание и дисперсия случайной величины Х, распределенной по закону Пуассона, m_x=a и D_x=a².

4. Закон равномерного распределения.

Рис. 3. Закон равномерного распределения

Если возможные значения непрерывной случайной величины X лежат в пределах некоторого определенного интервала [x₁, x₂] и, кроме того, известно, что в пределах этого интервала все значения X одинаково вероятны, то она распределена равномерно.

В этом случае плотность распределения

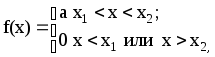
. ( 17 )

Математическое ожидание и дисперсия такой случайной величины Х,

, ( 18 )

. ( 19 )

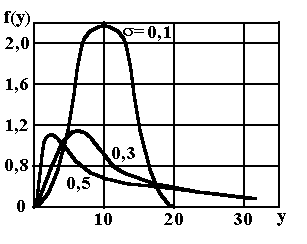
5. Закон логарифмически нормального распределения.

   Рассмотрим случайные величины x и y, связанные соотношением х = lg y. Если случайная величина х распределена нормально, то плотность распределения y равна

Рис. 4. Закон логарифмического распределения

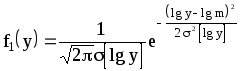. ( 20 )

Этот закон характерен для случайных величин, разброс которых вызван действием многих случайных факторов, которые перемножаются.

Характер поведения функции f(y) в зависимости от у для ряда значений s при lg m = 1 показан на рис. 4.

6. Закон гамма-распределения.

Рис. 5. Закон гамма-распределения

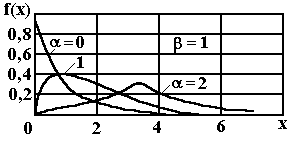
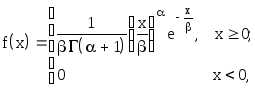(21)

где a > -1; b > 0; Г (a+1)=- гамма-функция .

Характерен для случайных величин, ограниченных слева (по минимуму), например, для длительности выполнения технологических операций.

Параметры гамма-распределения

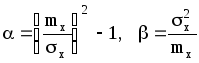. ( 22 )

При больших значениях параметра a гамма-распределение переходит в нормальное распределение. Если положить в b=1/l и a=k, где k-целое положительное число, то получим закон распределения Эрланга

, ( 23 )

а при k =1 получим экспоненциальный закон распределения

, ( 24 )

которые используют в теории надежности.

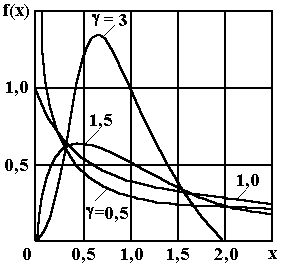
7. Закон распределения Вейбулла.

Рис. 6. Закон распределения Вейбулла.

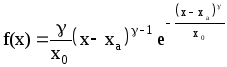, ( 25 )

где x_a, x₀ и g - параметры распределения.

В частном случае, когда x_a = 0 и x₀ = 1,

. ( 26 )

Характерен для случайных величин, ограниченных слева, например, для наработки системы на отказ, времени устранения отказа и других показателей теории надежности.

СВЯЗЬ МЕЖДУ СЛУЧАЙНЫМИ ВЕЛИЧИНАМИ

При изучении зависимости между двумя величинами, каждая из которых подвергается случайному рассеиванию (неконтролируемому разбросу), применяются методы корреляционного анализа. Корреляционный анализ изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру зависимости между рассматриваемыми величинами. Сопоставляя каждому значению одной величины x, среднее из соответствующих значений другой величины y, мы получаем функцию регрессии или просто регрессию y на x. Функция регрессии изображается графически линией регрессии.

Коэффициентом корреляции r_xy между случайными величинами x и y называется математическое ожидание произведения их нормированных отклонений:

, ( 27 )

. ( 28 )

Для независимых величин x и y коэффициент корреляции равен нулю. Но даже и для зависимых величин коэффициент корреляции может оказаться равным нулю (в этом случае величины x и y называются некоррелированными). Коэффициент корреляции характеризует меру линейной зависимости между величинами x и y.

r_xy = 0 означает отсутствие линейной зависимости (но не исключает зависимости нелинейной). Чем ближе ïr_xyï к 1, тем теснее линейная зависимость между величинами. Если r_xy > 0, то при возрастании x величина y тоже (в среднем) возрастает.

Для экспериментального изучения зависимости между двумя величинами x и y производят некоторое количество n независимых испытаний. Результат i–го испытания дает пару значений x_i, y_i. По этим значениям определяется эмпирический коэффициент корреляции:

. ( 29 )

Даже для независимых величин эмпирический коэффициент корреляции может оказаться отличным от нуля вследствие случайного рассеивания результатов измерения.

Значимость коэффициента корреляции проверяется путем сравнения его величины с ошибкой его оценки при заданной надежности вывода (доверительной вероятности) P.

С вероятностью p можно утверждать, что линейная корреляция значима, если |r^*_xy|>e_r, где e_r - ошибка оценки r_xy

, ( 30 )

где N - количество опытов,

t_c(N, p) - квантили распределения Стьюдента приведены в табл. 1.

Табл. 1

	0.9	0.95	0.99
5	1.48	2.02	3.37
10	1.37	1.81	2.76
20	1.33	1.73	2.53
40	1.30	1.68	2.42
120	1.29	1.66	2.36

Характер связи между случайными величинами x и y определяется уравнением регрессии. Уравнения линейной регрессии y на x (аналог функций y(x))

( 31 )

и регрессии x на y (аналог функций x(y))

. ( 32 )

Коэффициенты регрессии (угловые коэффициенты прямых регрессии)

. ( 33 )

Рис. 7. Прямые регрессии для обоих

уравнений регрессии

Коэффициенты регрессии b_y|x и b_x|y имеют тот же знак, что и коэффициент корреляции r. Обе прямые регрессии проходят через точку (m_x, m_y) - центр распределения (рис. 7).

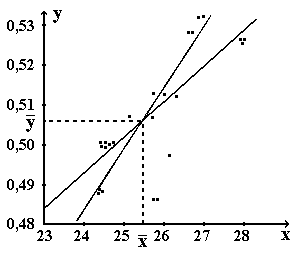
Коэффициенты уравнения регрессии удовлетворяют условию наименьших квадратов.

В случае нелинейной регрессии построение кривых регрессии проводится методом наименьших квадратов. Обычно ограничиваются параболическими зависимостями невысокого порядка, т.е. многочленами степеней 2 и 3.

Множественная корреляция описывает связь между тремя и более случайными величинами.

СЛУЧАЙНЫЕ ПРОЦЕССЫ

Случайной называют такую функцию, значение которой при каждом значении детерминированного аргумента является случайной величиной. Случайные функции X(t) времени называют случайными процессами (СП).

Для описания основных свойств случайного одномерного процесса используют неслучайные статистические характеристики:

• математическое ожидание СП - характеризует поведение процесса по времени в среднем, определяется по формуле (3), если n_i - последовательные отсчеты СП по времени;

• дисперсия СП - характеризует рассеяние значений функции относительно среднего значения, определяется по формуле (4);

• плотность распределения амплитуд СП;

• корреляционная функция - характеризует степень близости соседних значений СП;

• спектральная плотность - характеризует внутренние закономерности в СП.

Нестационарным СП называют такой процесс, статистические характеристики которого (хотя бы одна) изменяются во времени.

Рис. 8. Случайная функция X (t)

Автокорреляционная функция (АКФ) - мера связи любых двух ординат СП x(t_j) и x(t_l), отстоящих на абсциссу t = t_l - t_j. Для СП с неизменной АКФ (стационарного), АКФ не зависит от t и ее оценка по дискретным отсчетам

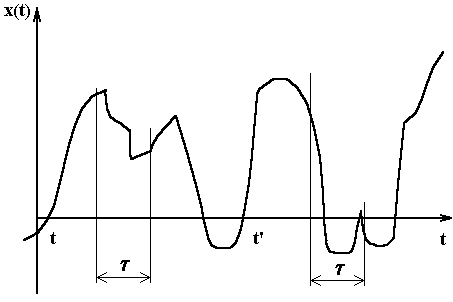
. (34)

Значение при t = 0 равно дисперсии СП K_xx(0) = D_x.

Нормированная АКФ , поэтомуk_xx(0) = 1.

СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СП

Периодическую функцию f(x) можно разложить в ряд Фурье (тригонометрический ряд)

, ( 35 )

где a₀ - среднее значение f(t) за период;

T - период функции f(t).

Коэффициенты ряда

,, . ( 36 )

Ряд Фурье в комплексной форме

, ( 37 )

где ,.

Набор частот w_k называют спектром функции f(t). В данном случае спектр - дискретный. Приближенный метод разложения в ряд Фурье для непериодической функции состоит в применении предельного перехода при T ® ¥. Действительно, непериодическую функцию можно рассматривать как периодическую при неограниченно возрастающем периоде.

Устремляя T к бесконечности и полагая, что , частотаDw₁ есть частотный интервал между соседними абсциссами - гармониками, частоты которых равны и. При предельном переходе получим, что приT ® ¥ Dw₁ ® dw, а ® w, где w - текущая частота, изменяющаяся непрерывно. Сумма в уравнении ( 37 ) перейдет в интеграл, тогда

, ( 38 )

где спектральная плотность СП

. ( 39 )

Формулы ( 38 ) и ( 39 ) - интегралы Фурье, являются основными формулами спектральной теории гармонического анализа СП.

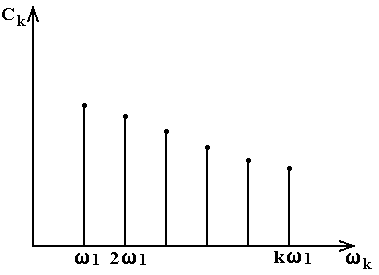
Функция f(t) в виде ( 38 ) имеет непрерывный спектр. Если ряд Фурье дает возможность представить периодическую функцию в виде суммы бесконечного числа синусоид с частотами, имеющими дискретные значения, то интеграл Фурье ( 39 ) представляет непериодическую функцию в виде суммы синусоид с непрерывной последовательностью частот. Спектр периодической функции можно изобразить графически (рис. 9). Каждому дискретному значению частоты (частоты w_k гармоник ряда Фурье) соответствует определенное значение коэффициента ряда c_k. Спектр, показанный на рис. 9, называют дискретным или линейчатым.

Рис. 9. Спектр периодической функции

Рассмотрим теперь спектр непериодической функции. В результате предельного перехода от ряда к интегралу Фурье интервалы между отдельными спектральными линиями неограниченно сокра-щаются, вертикальные линии гармоники все больше сближаются и в пределе получаем непрерывную кривую, для которой можно ввести обозначение S(w). Тогда комплексная амплитуда каждого отдельного колебания бесконечно мала

. ( 40 )

Из ( 40 ) следует, что S(w) есть амплитуда для интервала частот (w, w+Dw). Значит, S(w) можно рассматривать как «плотность» амплитуд, приходящихся на интервал частот (w, w+Dw). Поэтому функцию S(w) называют спектральной плотностью. S(w) > 0 при любом w.

Спектральная плотность и автокорреляционная функция связаны следующим образом

, ( 41 )

. ( 42 )