В В Е Д Е Н И Е

Сложность современного производства, разнообразие машин, агрегатов и технологических процессов, особые условия, в которых они протекают, увеличение скоростей обработки материалов и повышение требований к качеству готовой продукции делают во многих случаях невозможным управление агрегатами без систем автоматизации, так как человек не в состоянии быстро и эффективно реагировать на множество факторов, влияющих на ход процессов.

Общим направлением комплексной автоматизации и механизации является создание автоматизированных систем управления технологическими процессами (АСУ ТП) на основе применения широкой номенклатуры измерительных устройств, мини- и микроЭВМ, интегрированного управления.

При создании АСУ ТП возникает ряд взаимосвязанных задач, в решении которых необходимо участие технологов, механиков, математиков и других специалистов. Отсюда вытекает важность знания основ автоматизации.

Цель практических занятий и выполнения контрольных заданий - закрепление теоретических знаний и приобретение практических навыков разработки и расчета отдельных узлов автоматизированных систем управления, изучение АСУ ТП различных агрегатов, технических средств, необходимых для их реализации, овладение основами анализа функционирования систем управления.

Студенты дневной формы обучения выполняют задания на практических занятиях или в виде домашних заданий в рамках самостоятельной работы. Объем определяет преподаватель в зависимости от специальности.

Контрольная работа студентов заочной формы обучения включает 3 задания, отражающие основные разделы программы изучаемой дисциплины: основы теории автоматического управления, технические средства АСУ ТП, АСУ ТП в различных отраслях.

Количество контрольных заданий и степень сложности выбраны так, чтобы время на их выполнение в совокупности с необходимым временем для изучения теоретического материала не превышало времени, отведенного на изучение всего курса.

Приступать к выполнению контрольных и индивидуальных заданий следует после изучения соответствующих разделов дисциплины, ознакомления с примерами решения подобных задач, имеющимися в рекомендуемой литературе, а также в настоящих методических указаниях.

Контрольные задания выдаются студентам дневного отделения в течение семестра, а студентам заочного отделения на семестр, в котором изучается дисциплина, в период предшествующей ему сессии (на установочной лекции). Каждый студент получает индивидуальное задание. Номер варианта каждого задания контрольной работы определяет преподаватель.

После выполнения работы студентами заочного факультета она высылается в деканат для проверки. Если работа выполнена верно и в соответствии с заданием, студент допускается к ее защите. В случае наличия ошибок или выполнения работы не в соответствии с заданием работа возвращается для доработки или исправления ошибок. Защитить контрольную работу необходимо до экзамена по изучаемой дисциплине.

Пояснительная записка контрольной работы должна быть написана от руки в тетради. На первой странице помещается задание. Перечень используемой литературы приводится в конце записки. Ссылки на источник в тексте делаются сокращенно: в квадратных скобках указывается номер источника по списку. В отдельных случаях после указания источника приводится номер таблицы, рисунка или страницы, например, /3/, табл.8; /2/, рис.4; /4/, с.72. Не допускается никаких сокращений слов и обозначений, кроме принятых официальными источниками. Чертежи схем, графики и другие иллюстрации должны быть выполнены аккуратно, карандашом и содержать необходимые обозначения. В подрисуночных надписях необходимо раскрыть сокращенные обозначения, принятые в схеме.

1. Основы теории автоматического управления

Выполнение заданий этого раздела требует знаний основ теории автоматического управления, в особенности динамики линейных систем автоматического управления, анализа их устойчивости, знаний правил преобразования структурных схем и методов получения дифференциальных уравнений и передаточных функций элементов и систем автоматического управления в целом. Изучая этот материал, следует обратить внимание не только на математические утвержде­ния, но и на особенности их конкретного применения.

Варианты 1.01...1.10. Составить дифференциальное уравнение, найти пе­редаточную функцию RC-цепи (рис.1.1) и построить амплитудную и фазовую частотные характеристики (АЧХ, ФЧХ, АФЧХ). Значение параметров указаны в табл.1.1.

Литература: /1/, с.52-62.

Рис. 1.1. Схемы RC-цепей

Таблица 1.1

Параметры	Вариант
	1.01	1.02	1.03	1.04	1.05	1.06	1.07	1.08	1.09	1.10
Схема, рис.	1.1а	1.1б	1.1в	1.1а	1.1в	1.1б	1.1б	1.1в	1.1а	1.1б
R, кОм	0.11	0.21	0.36	0.43	0.56	0.63	1.0	1.1	1.2	1.3
C, мкФ	2.0	4.0	10.0	15.0	20.0	20.0	15.0	10.0	4.0	2.0

Краткие сведения из теории

Частотные характеристики получают при рассмотрении вынужденных дви­же­ний звена (системы), вызванных гармоническим воздействием на входе x(t)=A_вхsinwt, где A_вх - амплитуда; w=2p/T_к -угловая частота входных колебаний с периодом T_к. Если A_вх=1, то входное воздействие - единичное гармоническое. По окончании переходного процесса на выходе линейной системы устанавливаются гармонические колебания y(t)=A_выхsin(wt+f) той же частоты, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний на угол f(w). Изменение амплитуды и фазовый сдвиг являются функциями частоты и выра­жают динамические свойства элемента (системы). Если изменять частоту w от 0 до Ґ и определять установившиеся амплитуду и фазу входных колебаний для разных частот, можно получить зависимость от частоты соотношения амплитуд A(w)=A_вых(w)/A_вх(w) и сдвига фазы f(w)=f_вых(w)-f_вх(w). A(w) называют амплитудно-частотной характеристикой (АЧХ), f(w) - фазовой частотной характеристикой (ФЧХ).

Аналитически АЧХ и ФЧХ получают следующим образом. Если в передаточную функцию вместо p подставить jw, получим частотную передаточную функцию W(jw). Ее можно представить в виде

W(jw)=U(w)+jV(w)=A(w)e^jf(w),

где U(w) и V(w) соответственно действительная и мнимая части, причем

A²(w)=U²(w)+V²(w)

f(w)=arctg(V(w)/U(w)).

Рис.1.2. Амплитудно-фазовая частотная характеристика

На комплексной плоскости (см.рис.1.2) частотную передаточную функцию определяет годограф вектора ОА, длина (модуль) которого равен A(w), а аргумент (угол, образованный этим вектором с действительной положительной полуосью) f(w). Кривую, которую описывает конец вектора при изменении частоты от 0 до Ґ, называют амплитудно-фазовой частотной характеристикой (АФЧХ). Таким образом, АФЧХ - это совмещенная АЧХ и ФЧХ.

Пример 1.1. Вывести дифференциальное уравнение, построить АФЧХ, АЧХ и ФЧХ RC-цепи (см.рис.1.1,а) при условии, что R=5.1 кОм, C=2.0 мкФ.

Решение. На основании второго закона Кирхгофа

U_вх=U_R+U_C , (1.1)

где U_R, U_C - падение напряжения на резисторе и емкости соответственно, причем U_C=U_вых .

В соответствии с законами электротехники . Сделаем подстановки в уравнение (1.1) и преобразуем его:

или

, (1.2)

где T=RC - постоянная времени.

По условию R=5.1 кОм; C=2.0 мкФ. Тогда T=5.1·10³·2·10^-6@0.01с. Записы­ваем (1.2) в операторной форме:

U_вх(p)=(Tp+1) U_вых(p).

Откуда передаточная функция

Частотная передаточная функция

W(jw)=1/(Tjw+1).

Выделим действительную и мнимую части:

U(w)=1/(T²w²+1); (1.3)

V(w)=-Tw/(T²w²+1); (1.4)

; (1.5)

f(w)=arctg=-arctgTw. (1.6)

Подставляя значения w в диапазоне от 0 до Ґ в выражения (1.3)...(1.6), рассчитываем U(w), V(w), A(w) и f(w) и результаты заносим в табл.3.1. АЧХ, ФЧХ и АФЧХ приведены на рис.3.2.

Характеристики удобно построить, отложив частоту в логарифмическом масштабе.

Таблица 1.2

w,	1	20	50	100	200	500	1000	Ґ
lgw	0	1.3	1.7	2.0	2.3	2.7	3	Ґ
U(w)	0,99	0.96	0.8	0.5	0.2	0.04	0.01	0
V(w)	-0,01	-0.19	-0.4	-0.5	-0.4	-0.19	-0.1	0
A(w)	0,99	0.98	0.89	0.71	0.45	0.194	0.1	0
f(w), град.	-0,5	-11	-27	-45	-64	-78	-84	-90

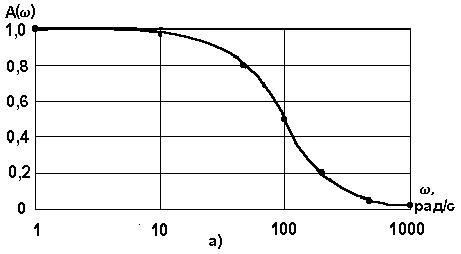
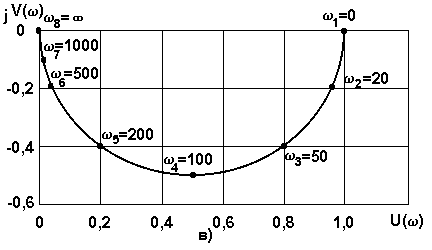
Рис.1.3. Частотные характеристики RC-цепи:

а) АЧХ, б) ФЧХ, в) АФЧХ

Варианты 1.11...1.20. Найти передаточную функцию соединения звеньев, построить амплитудно-фазовую частотную характеристику. Структурные схемы для различных вариантов приведены на рис.1.4, 1.5, 1.6, а передаточные функции отдельных звеньев - в табл. 1.3.

Литература: /1/, с. 70-76.

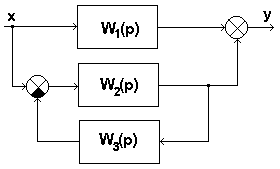
Рис.1.4. Структурная схема к вариантам 1.11...1.14

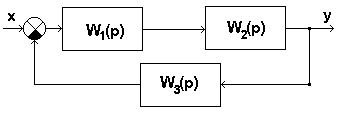
Рис.1.5. Структурная схема к вариантам 1.15...1.18

Рис.1.6. Структурная схема к вариантам 1.19...1.20

Таблица 1.3

Вари-	Передаточная функция					Структурная
ант	W1(p)	W2(p)	W3(p)	W4(p)	схема
1.11	3/(0.2p +1)	2/p	0.5	-	рис.1.4
1.12	1/(0.1p+1)	3/p	1.2	-	рис.1.4
1.13	3/(0.2p+1)	1/p	3.2	-	рис.1.4
1.14	1/(0.3p+1)	2/p	0.5	-	рис.1.4
1.15	3/(0.2p+1)	5/p	0.2	-	рис.1.5
1.16	1/p	0.5	0.5p	-	рис.1.5
1.17	0.2/p	0.5(0.2p+1)	1.0	-	рис.1.5
1.18	1/(p+1)	0.5/p	2.5	-	рис.1.5
1.19	4/p	0.2/p	0.1	1	рис.1.6
1.20	1/p	3/p	2	0.5	рис.1.6

Краткие сведения из теории

При решении вариантов 1.11...1.20 задания 1 следует, исходя из заданной структуры и передаточных функций отдельных звеньев, определить передаточную функцию их соединения. Для этого сначала следует выполнить преобразования структурной схемы, затем получить частотные передаточные функции и далее действовать так, как в предыдущем примере. Предварительно следует изучить раздел ТАУ "Соединение звеньев и преобразование структурных схем".

Пример 1.2. Построить АФЧХ соединения звеньев, приведенного на рис.1.4. W₁(p)=1/(0.3p+1); W₂(p)=5/p; W₃(p)=2.

Решение. Выполним преобразование структурной схемы. Звено 3 включено со звеном 2 встречно-параллельно (звено 3 является звеном обратной связи). Для случая отрицательной обратной связи имеем:

.

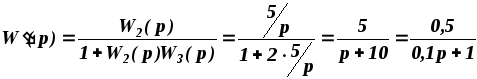Рис.1.7. Преобразованная структурная схема

Звенья W₁(p) и W_¢(p) согласно рис.1.7 включены параллельно. Таким образом, получили параллельное соединение двух инерционных звеньев. Частотная передаточная функция такого соединения равна сумме частотных передаточных функций звеньев, входящих в него. При этом сложение комплексов требует представления их в виде вещественной и мнимой частей.

Если W(jw)=U(w)+jV(w), то, соответственно

SW(jw)=SU(w)+jSV(w) (1.7)

W₁(jw);

;

Согласно (1.7)

Таким образом, для заданного соединения звеньев

U(w)=

V(w)= (1.8)

Представляя в выражении (1.8) значения w от 0 до Ґ, находим U(w) и V(w). По полученным значениям строим АФЧХ, как это показано в примере 1.1.

Можно также построить АФЧХ соединения звеньев путем суммирования векторов АФЧХ для одинаковых частот.

Пример 1.3. Построить АФЧХ соединения звеньев (рис.1.4), если W₁(p)=3/(0.2р+1); W₂(p)=2/р; W₃(p)=0,5.

Решение. После преобразования схемы получим схему, приведенную на рис.1.7 (см. предыдущий пример), где

W₁(p)=3/(0.2p+1); W'(p)=2/(p+1).

найдем значения U(w), U'(w), V(w) и V'(w) и занесем их в табл.1.4. Просуммировав графически векторы АФЧХ, получим результирующую характеристику, соответствующую суммарным значениям U(w) и V(w) (рис.1.8).

Таблица 1.4

Параметр	Значения частоты
	0	0.5	1.0	2.0	5.0	10	Ґ
U(w)	3.0	2.97	2.88	2.59	1.5	0.6	0
V(w)	0	-0.3	-0.58	-1.03	-1.5	-1.2	0
U'(w)	2.0	1.6	1.0	0.4	0.08	0.02	0
V'(w)	0	-0.8	-1.0	-0.8	-0.38	-0.2	0
SU(w)	5.0	4.57	3.88	2.99	1.58	0.62	0
SV(w)	0	-1.10	-1.58	-1.83	-1.68	-1.4	0

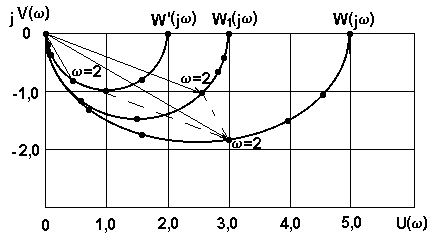
Рис.1.8. АФЧХ (к примеру 1.3)

Варианты 1.21...1.30. По функциональной схеме (рис.1.9) следящей системы управления приводом барабана летучих ножниц составить структурную схему и проверить систему на устойчивость по критерию Гурвица или Михайлова. Двигатель совместно с системой управления описывается дифференциальным уравнением

Передаточная функция тахогенератора с фильтром

w - частота вращения, рад/с;

T_1, T_2, T₃ - постоянные времени, с;

k_д - коэффициент передачи двигателя, рад/с.В;

k_тг - коэффициент передачи тахогенератора, с.В/рад.

Значения указанных параметров для различных вариантов приведены в табл.1.5.

Литература: /1/, с.117-129.

Рис.1.9. Функциональная схема следящей системы:

1- прокатная клеть; 2- барабан; ТГ1, ТГ2- тахогенераторы;

Д - двигатель; СУ- система управления приводом

Таблица 1.5

Вариант	Значение параметров
	T1, с	T2, с	kд, рад/с.в	kтг с.в/рад.	T3, с
1.21	0.1	0.2	1	2	0,01
1.22	0.5	0.2	1	5	0.01
1.23	0.4	0.1	2	10	0.02
1.24	0.2	0.1	3	2	0.02
1.25	0.3	0.2	0.5	1	0.01
1.26	0.1	0.2	10	2	0.005
1.27	0.5	0.25	4	4	0.01
1.28	0.1	0.2	4	8	0.005
1.29	0.2	0.1	3	3	0.01
1.30	0.5	0.2	4	2	0.01

Варианты 1.31...1.40. Из условия устойчивости определить предельный (критический) коэффициент усиления электромеханической системы автомати­че­ского регулирования. Передаточные функции системы в разомкнутом состоянии и ее параметры приведены в табл.1.6.

Литература:/1/,с.117-129.

Таблица 1.6

Вариант	Передаточная функция	Значение параметров
		Т1, с	Т2, с	Т3, с
1.31		0.1	0.2	-
1.32	W(p)=k/p(T1p+1)(T2p+1)	0.2	0.2	-
1.33		0.3	0.4	-
1.34		0.1	0.2	0.3
1.35	W(p)=k/(T1p+1)(T2p+1)(T3p+1)	0.2	0.2	0.3
1.36		0.2	0.3	0.4
1.37		0.1	0.2	-
1.38	W(p)=k/p(T12p2+T2p+1)	0.5	0.2	-
1.39		0.4	0.1	-
1.40		0.5	0.25	-

Варианты 1.41...1.50. По функциональной схеме регулятора положения нажимных винтов прокатной клети (рис.1.10) составить структурную схему и проверить систему на устойчивость по критерию Михайлова. Передаточная функция датчика положения W_дп(p)=k_дп. Передаточная функция предварительного усилителя (У) совместно с передаточной функцией тиристорного преобразователя (ТП) W_тп(p)=k_тп/(T₁p+1), а передаточная функция двигателя W_дв(p)=k_дв/(T₂²p²+2xT₂p+1), где x -коэффициент демпфирования. Передаточный коэффициент редуктора k_р=1/i, где i -передаточное число редуктора. Выходной сигнал - угол поворота нажимного винта f. Значения параметров - в табл.1.7.

Литература: /1/, с.82-85; 117-129.

Краткие сведения из теории

Одним из основных условий работоспособности АСР является ее устойчивость, т.е. способность системы возвращаться в исходное состояние после снятия воздействия, выведшего ее из этого состояния.

Необходимым и достаточным условием устойчивости системы является отрицательность вещественной части комплексных корней характеристического уравнения. Характеристическое уравнение получают обычно, приравнивая к нулю дифференциальный оператор при выходной величине в исходном дифференциальном уравнении.

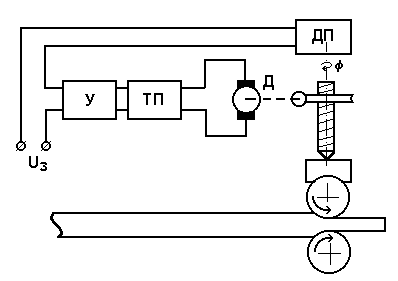
Рис.1.10. Функциональная схема регулятора положения

нажимных винтов: У - предварительный усилитель;

ТП - тиристорный преобразователь; Д - двигатель;

ДП - датчик положения нажимных винтов

Таблица 1.7

Вариант	Значения параметров
	kдп, В/рад	kтп	T1, с	T2, с	x	kдв, рад/с В	i
1.41	2	20	0.01	0.1	1.0	1	80
1.42	2	20	0.01	0.2	1.0	1	80
1.43	2	10	0.03	0.1	1.2	1	80
1.44	3	8	0.01	0.5	1.2	4	24
1.45	3	4	0.01	0.2	1.2	6	20
1.46	3	6	0.02	0.5	1.3	6	20
1.47	1	40	0.02	0.1	1.3	2	55
1.48	1	30	0.03	0.2	1.2	1	80
1.49	1	30	0.03	0.2	0.8	2	24
1.50	0.5	50	0.02	0.2	0.8	1	55

Вычисление корней весьма просто лишь для характерестического уравнения первой и второй степени. Существуют общие выражения для корней уравнений третьей и четвертой степени, но эти выражения громоздки и практически не применяются. Для уравнений более высоких степеней вообще невозможно написать общие выражения для корней через коэффициенты характерестического уравнения.

Существуют правила, позволяющие определять устойчивость системы без вычисления корней. Эти правила называют критериями устойчивости. Существует несколько критериев устойчивости. Все они математически эквивалентны, так как решают вопрос о знаке вещественной части корней характерестического уравнения. Их разделяют на алгебраические и частотные.

Алгебраические критерии позволяют судить об устойчивости системы по коэффициентам многочлена

D(p)=a_npⁿ+a_n-1p^n-1+...+a₁p+a₀ (1.9)

Во-первых, необходимым (но, недостаточным!) условием устойчивости является положительность всех коэффициентов a_n,...,a₀. Если хотя бы один из коэффициентов меньше нуля, то система неустойчива и дальнейшее исследование не имеет смысла. Если a_n>0, a_n-1>0,..., a₀>0, то согласно алгебраическому критерию устойчивости Гурвица система устойчива, если все определители Гурвица больше нуля. Для коэффициентов многочлена (1.9) составляют квадратную матрицу nґn, по главной диагонали которой записывают все коэффициенты от a_n-1 до a₀ и далее заполняют ее, как показано ниже. В случае отсутствия данного коэффициента и если его номер больше n или меньше нуля, на его место проставляют нуль. В главной диагонали определителя оказываются последовательно все коэффициенты, кроме a_n.

Определители Гурвица составляют так:

D₁=a_n-1>0;

и т.д.

Последний определитель включает всю матрицу. Но каждый последующий определитель может быть вычислен через предыдущий. Так как в устойчивой системе D_n-1>0, то положительность последнего определителя обеспечивается, если a_0>0.

Рассмотрим критерий Гурвица для нескольких конкретных значений n.

Для n=1

D(p)=a₁p+a₀,

и условие устойчивости сводится к неравенствам

a₁>0; a₀>0.

Для n=2

D(p)=a₂p²+a₁p+a₀,

Условие устойчивости :

a₂>0; a₁>0; a₀>0.

Например, звено с передаточной функцией k/(T₂²p²+T₁p+1) устойчиво, если перед всеми членами в знаменателе стоит знак плюс.

Если n=3, то

D(p)=a₃p³+a₂p²+a₁p+a₀,

В этом случае условия устойчивости :

a₃>0; a₂>0;

D₃=a₀D₂>0.

Если D₂>0, то a₀>0. Т.о. условие устойчивости сводится к положительности всех коэффициентов и предпоследнего минора D₂. Критическое значение коэффициента усиления может быть найдено из выражения

a₂a₁=a₃a_0,

где a₀ включает предельный коэффициент усиления k_пр (см. пример 1.5).

Для n=4

D(p)=a₄p⁴+a₃p³+a₂p²+a₁p+a₀,

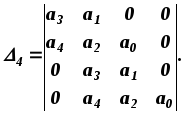
Условия устойчивости :

a₄>0; a₃>0; D₂=a₃a₂-a₄a₁>0;

D₃=a₁D₂-a₃²a₀>0; D₄=a₀D₃>0.

Таким образом, условия устойчивости опять сводятся к требованию положительности всех коэффициентов и предпоследнего минора D₃. (Условие D₂>0 при этом вытекает из неравенства D₃>0 с учетом того , что D₄>0 ).

В общем случае системы n-го порядка необходимым условием устойчивости является требование положительности всех коэффициентов. Анализ устойчивости надо начинать с проверки этого простого условия. Если оно не выполняется, то отпадает необходимость в составлении и проверке остальных неравенств.

Для характеристических уравнений невысоких порядков применение алгебраических критериев достаточно просто. Если же уравнение имеет высокий порядок, то применить алгебраические критерии затруднительно. Если система включает звено запаздывания, то характеристическое уравнение становится трансцендентным из-за члена e^-pt.

В подобных случаях используют частотные критерии. Они удобны в силу простоты геометрической интерпретации и наглядности .

Согласно критерию Михайлова для устойчивости системы необходимо и достаточно, чтобы с ростом w от 0 до Ґ годограф Михайлова, начинаясь на положительной части действительной оси, обходил последовательно n квадрантов, где n - порядок характеристического полинома

D(p)=a_npⁿ+a_n-1p^n-1+...+a₀.

На рис.1.11 показаны кривые Михайлова для устойчивых систем различных порядков.

Рис.1.11. Кривые Михайлова для устойчивых систем

Пример 1.4. Система описывается дифференциальным уравнением

где х, у - соответственно входная и выходная величины;

T₁=0,02 c; T₂=0,5 c; T₃=0,2 c - постоянные времени; k=5 - коэффициент усиления. Проверить систему на устойчивость по критерию Гурвица.

Решение. Запишем передаточную функцию разомкнутой системы, соответствующую заданному дифференциальному уравнению:

(1.10)

Характеристический многочлен замкнутой системы

D(p)=a₃p³+a₂p²+a₁p+a₀,

где: a₃=T₃³; a₂=T₂²; a₁=T₁; a₀=k+1, т.е.

a₃=0,008; a₂=0,25; a₁=0,2; a₀=6.

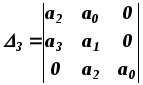
D₂=a₂a₁-a₃a₀=0,050-0,048>0.

Условия устойчивости a₃>0, a₂>0, a₁>0, a₀>0 и D₂>0 выполняются.

Таким образом, система с передаточной функцией (1.10) устойчива, если при положительности всех коэффициентов произведение a₂a₁ больше произведения a₃a_0.

Для того, чтобы повысить точность статической системы регулирования, т.е. снизить статическую ошибку, необходимо увеличить коэффициент передачи системы. Однако, для существенного уменьшения статического отклонения при этом требуется увеличить коэффициент передачи до очень больших величин. Технически это реализовать возможно, однако на величину коэффициента усиления накладывается ограничение по условию устойчивости. В связи с этим определение предельного коэффициента усиления имеет важное практическое значение. Определение предельного коэффициента усиления равносильно определению условия нахождения системы на границе устойчивости .

Для того, чтобы найти предельный коэффициент усиления, необходимо выполнить анализ характеристического уравнения.

Пример 1.5. Пусть задана передаточная функция разомкнутой системы

W(p)=k/(T₁p+1)(T₂p+1)(T₃p+1).

В этом случае

D(p)=(T₁p+1)(T₂p+1)(T₃p+1)+k, (1.11)

что соответствует замкнутой системе регулирования, содержащей три инерционных звена с общим коэффициентом усиления k. Необходимо определить предельное значение k_пр, при котором система перестает быть устойчивой.

Решение. Перепишем (1.11) в виде

D(p)=T₁T₂T₃p³+(T₁T₂+T₁T₃+T₂T₃)p²+(T₁+T₂+T₃)p+1+k,

или

D(p)=a₃p³+a₂p²+a₁p+a₀,

где a₃=T₁T₂T₃; a₂=T₁T₂+T₁T₃+T₂T₃; a₁=T₁+T₂+T₃; a₀=1+k.

Согласно критерию Гурвица система устойчива, если выполняются неравенства

а₃>0, D₁=a₂>0, D₂=a₂a₁-a₃a₀>0; D₃=a₀D₂>0,

т.е. если, при условии положительности всех коэффициентов, выполняется неравенство

a₂a₁>a₃(1+k), где (1+k)=a₀. (1.12)

Неравенство (1.12) можно переписать в виде

k<a₂a₁/a₃ - 1.

Это неравенство нарушится при

kіk_пр=a₂a₁/a₃ - 1. (1.13)

Пусть, например, T₁=0,2 с; T₂=0,1 с; T₃=0,5 с.

Тогда

a₃=T₁T₂T₃=0,2•0,1•0,5=0,01;

a₂=T₁T₂+T₁T₃+T₂T₃=0,2•0,1+0,2•0,5+0,1•0,5=0,17;

a₁=T₁+T₂+T₃=0,2+0,1+0,5=0,8.

Согласно (1.13)

k_пр=a₂a₁/a₃ - 1=0,17•0,8/0,01-1=12,6.

Пример 1.6. Характеристический многочлен замкнутой системы такой же, как и в предыдущем примере. Определить предельный коэффициент усиления, применив критерий устойчивости Михайлова.

Решение. Представим (1.11) в виде

D(p)=(T₁p+1)(T₂p+1)(T₃p+1)+k=A(p)+k.

Для решения задачи следует построить годограф Михайлова

D(jw)=A(jw)+k.

Для этого вначале построим годограф

A(jw)=(T₁jw+1)(T₂jw+1)(T₃jw+1). (1.14)

Преобразуем (1.14) к виду A(jw)=U(w)+jV(w), где

U(w)=1-a₂w²;

V(w)=w(a₁-a₃w²).

Подставив значения из предыдущего примера, получим

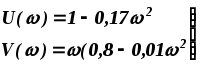(1.15)

Задаваясь значениями w в диапазоне от 0 до Ґ, рассчитываем значения U(w) и V(w). Результаты расчета сводим в табл. 1.8.

Таблица 1.8.

w, с-1	0	1,0	2,0	3,0	4,0	5,0	6,0	8,94	20,0	Ґ
U(w)	1	0,83	0,32	-0,53	-1,72	-3,25	-5,12	-12,6	-67	-Ґ
V(w)	0	0,79	1,52	2,13	2,56	2,75	2,64	0	-64	-Ґ

При частоте w=8,94, как следует из (1.15), V(w)=0, т.е. годограф пересекает действительную ось.

Годограф A(jw) показан на рис. 1.12.

Для того, чтобы получить годограф D(jw), достаточно мнимую ось сместить влево на величину k. Из рис.1.12 следует, что система находится на границе устойчивости, если значение равно значению k_пр, при котором годограф D(jw) пройдет через начало координат. Cогласно рис.1.12 величина k_пр=12,6, что совпадает с результатом предыдущей задачи.

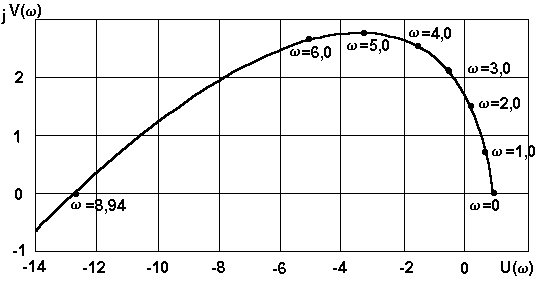
Рис.1.12. К определению предельного коэффициента усиления

Варианты 1.51…1.75. Выбрать простейший регулятор, обеспечивающий поддержание заданных параметров переходного процесса, и определить его настройки для стабилизации температуры в сварочной зоне методической нагревательной печи, имеющей запаздывание t_об, постоянную времени Т_об, коэффициент передачи k_oб и максимальное возмущающее воздействие x_вх. Технологические требования: допустимая статическая ошибка не должна превышать Dx_ст^доп; максимальное динамическое отклонение - x₁^доп; допустимое время регулирования - t_р^доп в соответствии с заданным типовым законом (табл. 1.9). Проверку соответствия качества системы заданным требованиям выполнить на ПЭВМ с использованием прикладного пакета моделирования.

Табл. 1.9.

№ вар	Dxстдоп, °С	x1доп, °С	tрдоп, с	tоб, с	Тоб, с	koб,°С /% хода РО	xвх, % хода РО	Типовой закон
1.51	10	20	400	50	230	2.8	25	20% перерег.
1.52	15	15	250	52	235	2.5	25	апериодич.
1.53	10	20	550	54	240	2.6	25	min òx2dt
1.54	15	25	750	56	220	2.7	25	20% перерег.
1.55	10	20	300	58	225	2.8	25	апериодич.
1.56	15	15	670	60	300	2.9	25	min òx2dt
1.57	10	30	480	60	235	2.5	25	20% перерег.
1.58	10	25	450	50	240	3.1	25	апериодич.
1.59	15	25	590	52	220	2.8	25	min òx2dt
1.60	15	15	440	54	225	2.8	25	20% перерег.
1.61	10	20	280	56	230	2.5	25	апериодич.
1.62	15	25	640	58	235	2.6	25	min òx2dt
1.63	10	20	500	60	240	2.7	25	20% перерег.
1.64	15	25	350	60	220	2.8	25	апериодич.
1.65	10	20	650	58	225	2.9	25	min òx2dt
1.66	15	25	450	56	230	2.4	25	20% перерег.
1.67	15	20	390	54	235	3.1	25	апериодич.
1.68	10	25	580	52	240	2.6	25	min òx2dt
1.69	10	20	650	50	220	2.6	25	20% перерег.
1.70	15	25	350	48	225	2.5	25	апериодич.
1.71	10	20	600	54	230	2.6	25	min òx2dt
1.72	15	15	410	50	235	2.7	25	20% перерег.
1.73	10	20	470	52	240	2.8	25	апериодич.
1.74	15	25	550	54	220	2.9	25	min òx2dt
1.75	10	25	450	56	225	2.5	25	20% перерег.

Краткие сведения из теории

Автоматический регулятор - это комплекс устройств, подключаемых к объекту регулирования и обеспечивающих автоматическое поддержание заданных значений его регулируемых величин или автоматическое изменение их по определенному закону.

Определяющим условием при выборе регулятора и расчета его настроек является качество регулирования, определяющее точность поддержания технологического режима и ее экономическую эффективность. При этом под выбором регулятора понимают выбор закона регулирования.

Закон регулирования - это математическая зависимость между входной и выходной величинами регулятора.

Наиболее широкое распространение получили регуляторы непрерывного действия, использующие линейные законы регулирования

,

где x _вых.р - выходная величина регулятора;

x_вх.р - его входная величина;

C₁, C₂, C₃ - коэффициенты пропорциональности, называемые параметрами настройки регулятора;

t - время.

Сумма трех составляющих образует ПИД-закон регулирования. При отсутствии отдельных составляющих будут образовываться П-, И-, ПИ-, ПД-законы регулирования. В соответствии с реализуемыми законами регулирования регуляторы непрерывного действия делятся на различные типы.

1. Пропорциональные регуляторы, у которых выходная величина x_вых.р связана с входной величиной x_вх.р соотношением

x_вых._р = k_рx_вх._р,

где k_р - коэффициент передачи регулятора.

Передаточная функция П-регулятора имеет вид

W_п(p) = k_р.

2. Интегральные регуляторы, у которых изменение выходной величины пропорционально интегралу изменения входной

,

где k_р1 - коэффициент передачи И-регулятора, характеризующий скорость исполнительного механизма при отклонении входной величины.

Передаточная функция И-регулятора

W_и(p) = k_р1/p.

3. Пропорционально-интегральные регуляторы, у которых изменение выходной величины пропорционально как изменению входной величины, так и интегралу ее изменения

,

где T_и - время изодрома.

Передаточная функция такого ПИ-регулятора

.

4. Пропорционально-дифференциальные регуляторы, которые оказывают суммарное воздействие на регулирующий орган, пропорциональное как отклонению регулируемой величины, так и скорости ее отклонения

,

где T_п - время предварения.

Передаточная функция регулятора имеет вид

W_пд(p)=k_р(1+T_пp).

5. Пропорционально-интегрально-дифференциальные регуляторы, у которых изменение выходной величины пропорционально отклонению регулируемой величины, интегралу этого изменения и скорости изменения этой величины

.

Передаточная функция ПИД-регулятора

В соответствии с законами регулирования настройками этих регуляторов являются:

для П-регулятора - коэффициент передачи k_p, % хода регулирующего органа/единица измерения регулируемой величины;

для И-регулятора - коэффициент передачи k_р1, % хода регулирующего органа/с×единица измерения регулируемой величины;

для ПИ-регулятора - коэффициент передачи k_p, % хода регулирующего органа/единица измерения регулируемой величины; время изодрома T_и, с;

для ПИД-регулятора - коэффициент передачи k_p; время изодрома T_и, с; время предварения T_п, с.

Настройки непрерывных регуляторов П-, И-, ПИ-, и ПИД-действия позволяют получить любой из трех типовых оптимальных процессов регулирования: апериодический процесс с минимальным временем регулирования, с 20%-ным перерегулированием или процесс с минимальной квадратичной площадью отклонения с min òx²dt.

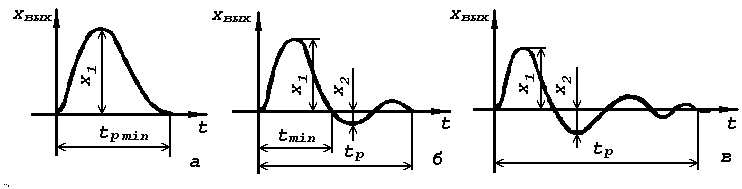
Рис. 1.13. Типовые переходные процессы регулирования

Апериодический процесс (граничный) с минимальным временем регулирования, кроме минимальной величины общего времени регулирования t_р, характеризуется отсутствием перерегулирования и минимальным регулирующим воздействием. Применяют тогда, когда требуется минимальное время регулирования, перерегулирование не допускается, а динамическое отклонение x₁ может быть сравнительно большим (рис. 1.13, а).

Процесс с 20%-ным перерегулированием и минимальным временем первого полупериода колебаний рекомендуется применять в тех случаях, когда допускают определенную величину перерегулирования, но предъявляют более жесткие, чем в предыдущем случае, требования к величине максимального динамического отклонения регулируемой величины (рис. 1.13, б).

Процесс с min òx²dt - процесс с минимальной квадратичной площадью отклонения характеризуется наибольшим перерегулированием (40 - 45%) и временем регулирования, а также наибольшим регулирующим воздействием, но и наименьшей величиной динамического отклонения (рис. 1.13, в).

Регулятор выбирается по известным характеристикам объекта регулирования и возмущения и при заданных требованиях, предъявляемых к качеству переходных процессов. Сначала следует выбрать тип регулятора, затем закон регулирования и соответствующие параметры его настроек.

С приемлемой для практических целей точностью большинство объектов регулирования в черной металлургии можно аппроксимировать статическим объектом с запаздыванием:

или астатическим объектом с запаздыванием

.

Исходными данными для выбора регулятора являются:

1. Статические и динамические параметры объекта регулирования, определяемые по кривой разгона: чистое запаздывание t_об; постоянная времени Т_об; их отношение t_об/Т_об; коэффициент передачи k_oб.

2. Максимально возможные значения возмущений по нагрузке x_вх, % хода регулирующего органа, - пиковых, скачкообразных длительных и непрерывных монотонных (при непрерывных возмущениях должна быть известна также максимальная скорость возмущения х'_вх, %/с).

3. Требуемые показатели качества регулирования объекта. При установке регулятора непрерывного действия должны обеспечиваться: максимальное динамическое отклонение x₁^доп (единицах измерения регулируемой величины); допустимое или желаемое перерегулирование x₂^доп/x₁^доп, %; допустимое остаточное отклонение (статическая ошибка) Dx_ст^доп (единицах измерения регулируемой величины); предельно допустимое время регулирования t_р^доп, с.

При инженерных методах выбора и расчета регуляторов закон регулирования и значение настроек регулятора могут быть определены по следующей методике:

1. Определить тип регулятора по величине отношения t_об/T_об.

tоб/Tоб	< 0.2	< 1.0	> 1.0
Тип регулятора	Релейный	Непрерывный	Импульсный или непрерывный

2. Рассчитать величину допустимого динамического коэффициента регулирования

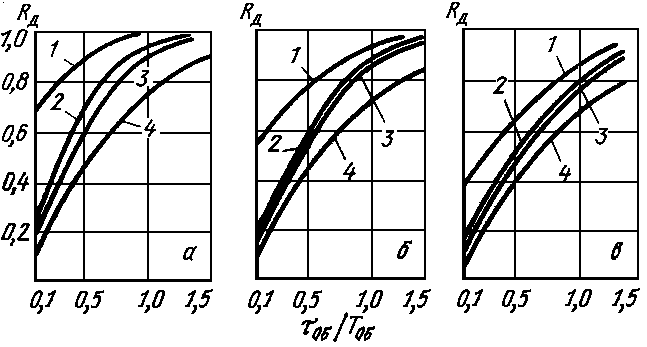
Рис. 1.14. Динамические коэффициенты регулирования на статических объектах при процессах: а - апериодическом; б - с 20%‑ным перерегулированием; в - с min òx²dt; 1 - И-регулятор; 2 - П-регулятор; 3 - ПИ-регулятор; 4 - ПИД-регулятор

3. По графикам R_д(t_об/T_об), приведенным на рис. 1.14 для заданного типового оптимального процесса регулирования, выбрать простейший регулятор (закон регулирования), обеспечивающий при заданном значении t_об/T_об значение динамического коэффициента регулирования R_д £ R_д^доп.

4. По графикам, приведенным на рис. 1.15 для статических ОР, проверить, обеспечит ли выбранный регулятор допустимое время регулирования t_р.

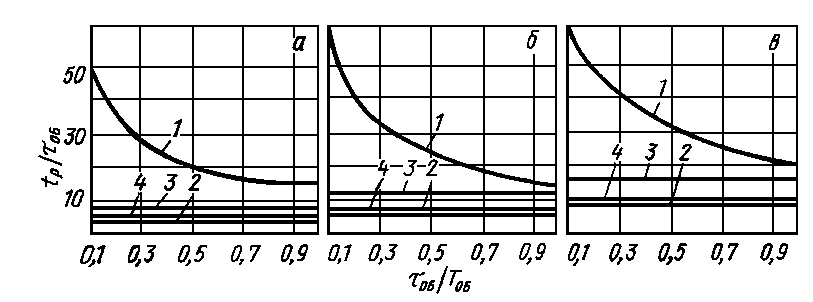
Рис. 1.15. Время регулирования на статических объектах:

а - апериодический процесс; б - процесс с 20%-ным перерегулированием; в - процесс с min òx²dt; 1 - 4 - соответственно И-, П-, ПИ, ПИД-регуляторы

5. Для П-регулятора, необходимо по рис. 1.16 найти величину статической ошибки, и если она больше допустимой, то вместо П-регулятора нужно установить более сложный регулятор.

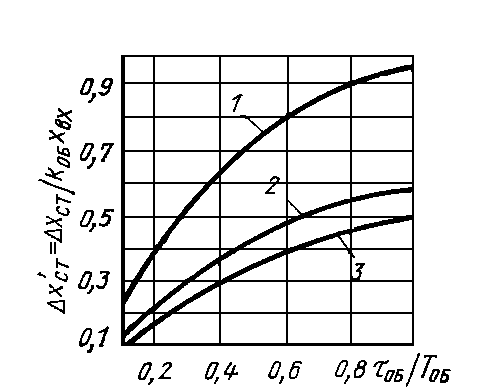
Рис. 1.16. Остаточное отклонение на статических объектах:

1 - апериодический процесс; 2 - процесс с 20%-ным перерегулированием; 3 - процесс с min òx²dt

6. Для выбранного регулятора подсчитать значения настроек по формулам, приведенным в табл. 1.10.

Табл. 1.10.

	Типовой переходной процесс
Регулятор	апериодический	с 20%-ным перерегулированием	с min òx2dt
И	;	;	;
П	;	;	;
ПИ	; Ти = 0.6Тоб;	; Ти = 0.7Тоб;	; Ти = Тоб;
ПИД	; Ти=2.4tоб; Тп=0.4tоб.	; Ти=2.0tоб; Тп=0.4tоб.	; Ти=1.3tоб; Тп=0.5tоб.