
Konspekt_VPA
.pdf
ефективності проекту слід враховувати зміну цінності грошей у часі. Прийоми, за допомогою яких це здійснюється, розроблені у межах фінансової математики. Для аналізу проектів доцільно розглянути ключові з них.
Концепція оцінки грошей у часі ґрунтується на тому, що вартість грошей з плином часу змінюється з урахуванням норм прибутку на ринку грошей.
У процесі порівняння вартості коштів застосовують два поняття: майбутня вартість коштів (future value – FV) та теперішня вартість коштів (present value – PV) (рис. 5.1).
|
Теперішній час |
|
|
|
|
|
Майбутній час |
|
|
|
|
|
Нарощування |
|
|
|
|
|
|
|
|
|
|
|
||
Початкова сума боргу |
|
(нагромадження, |
Кінцева сума боргу (S) – |
|||||
|
нарахування) |
|||||||
|
(Р) |
|
|
нарощена (нарахована) |
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
сума |
|
|
Ставка (і) |
|
|
|
|
|
|
|
|
|
|
|
Дисконтування |
|
|
|
|
|
|
|
|
|
|
|
||
Початкова сума боргу |
|
(компаундування, |
|
|
|
|||
|
приведення) |
|
Кінцева сума боргу (S) |
|||||
|
(Р) – приведена |
|
|
|||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
(дисконтована) сума |
|
|
|
|
Ставка (і) |
|||
|
|
|
|
|
|
|
||
|
|
|
|
|||||
|
Рис. 5.1. Взаємозв’язок між вартістю грошей у теперішньому та |
|||||||
|
|
|
|
майбутньому часі |
|
|
|
|
Майбутня вартість грошей (FV) являє собою суму інвестованих у теперішній момент коштів, в яку вони мають перетворитися через певний проміжок часу з урахуванням певної ставки відсотка.
Під ставкою відсотка розуміють вимір часової вартості грошей, суму відсотка на інвестиції, яка може бути отримана за даний період часу.
i |
I |
100 , |
(5.1) |
|
P |
||||
|
|
|
де І – абсолютна величина доходу від надання грошей в борг, Р – початкова сума боргу, що надається у користування на деякий час n за умови, що буде повернуто кінцеву суму боргу S.
51
I S P . |
(5.2) |
Часовий інтервал до якого відноситься ставка відсотка називається період нарахування. Найчастіше нарахування здійснюється за рік.
Розмір відсоткової ставки залежить як від об’єктивних, так і від суб’єктивних факторів, зокрема від загального стану економіки, в тому числі грошово-кредитного ринку, короткострокових і довгострокових очікувань його динаміки, виду угоди, її валюти, терміну кредиту, особливостей позичальника і кредитора.
Якщо інвестування здійснюється у короткому проміжку часу, то користуються простим відсотком – сумою, яку нарахована на первинну
вартість вкладу в кінці одного періоду. Він обчислюється за формулою: |
|
I p i n , |
(5.3) |
де I – грошовий вираз відсотка, сума процентних грошей, які нарахована за період інвестування; p – первинна вартість вкладу; i – відсоткова ставка; n – кількість періодів платежів.
Майбутня вартість грошей розраховується таким чином: |
|
FV = PV + I, |
(5.4) |
де PV – теперішня вартість грошей.
Якщо інвестування здійснюється у тривалому проміжку часу, то користуються складним відсотком.
Складний відсоток – це сума доходу, яка утворюється в результаті інвестування за умови, що сума нарахованого відсотка не виплачується після кожного періоду, а приєднується до суми основного вкладу і у подальшому платіжному періоді сама приносить дохід.
Процес переходу від теперішньої вартості (PV) до майбутньої (FV) називається компаундуванням.
Компаундування (нарахування) – операція, що дозволяє визначити
величину остаточної майбутньої вартості за допомогою складних відсотків: |
|
FV = PV(1 + i)n, |
(5.5) |
52 |
|
де FV – майбутня вартість коштів; PV – теперішня вартість коштів; i – ставка відсотка у поточному, або реальному виразах; n – кількість років або термін служби проекту; (1 + i)n – коефіцієнт (фактор) майбутньої вартості для i та n.
Процес дисконтування являє собою операцію, протилежну компаундуванню (нарощуванню складних відсотків) при обумовленому кінцевому розмірі коштів.
Дисконтування – процес визначення теперішньої вартості потоку готівки шляхом коригування майбутніх грошових надходжень за допомогою коефіцієнта дисконтування.
Теперішня вартість грошей (PV) являє собою суму майбутніх грошових надходжень, що наведені з урахуванням певної відсоткової ставки до теперішнього періоду:
|
|
PV |
FV |
, |
(5.6) |
|
|
|
|||
|
|
(1 i)n |
|||
де |
1 |
– коефіцієнт дисконтування. |
|
|
|
|
|
|
|
||
(1 i)n |
|
|
|
5.2. Розрахунки за допомогою простих і складних відсотків. Відомі дві схеми нарахування відсотків: за допомогою простих і складних відсотків. Прості відсотки використовуються, якщо база нарахування залишається не змінною, а складні – якщо база нарахування зростає на нараховану суму.
Отже, якщо сума Р надана в борг на n років під річну процентну ставку і,
то:
- за схемою простих відсотків щороку кінцева сума боргу зростатиме на величину P i , і в кінці періоду становитиме:
S P (1 i n) , |
(5.7) |
-за схемою складних відсотків чергові відсотки будуть нараховані не лише
зпочатком суми боргу, а з сумарної, до складу якої входять і раніше нараховані та не вилучені відсоткові гроші. Відбувається капіталізація відсотків. Отже, кінцева сума боргу буде становити:
за перший рік: S1 P P i P (1 i) ; |
|
(5.8) |
|||||||
за другий рік: S |
2 |
S |
S |
i S |
(1 i) P (1 i)2 |
; |
(5.9) |
||
|
|
|
1 |
1 |
1 |
|
|
|
|
за n років: S |
n |
P (1 i)n . |
|
|
|
(5.10) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
53 |
|
|
|
|
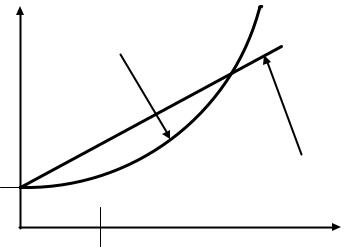
Вказані залежності, а саме |
S P (1 i) |
та |
S P (1 i)n |
є базовими |
|
формулами нагромадження за простими та складними відсотками відповідно. |
|||||
Для обґрунтування використання певної схеми нарахування відсотків |
|||||
доцільно проаналізувати співвідношення кінцевих сум, отриманих при |
|||||
нарахуванні за простими (Sпр) та за складними відсотками (Sскл). |
|
||||
Порівняємо множники (1 i n) та |
(1 i)n . Зрозуміло, що при n = 1 ці |
||||
величини збігаються та дорівнюють 1 + i. |
|
|
|
||
Якщо 0 n 1, то (1 i n) (1 i)n , |
якщо n 1, |
то (1 i n) (1 i)n . Отже, |
|||
при позиках до одного року ( 0 n 1) |
нарахована сума зростає швидше за |
||||
простими відсотками – Sпр > Sскл, а при позиках більше року – за складними Sпр |
|||||
< Sскл. (рис. 5.2). |
|
|
|
|
|
y |
(1 i)n |
|
|
|
|
y |
|
|
|
||
|
|
|
y (1 i n) |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
|
|
|
|
Рис. 5.2. Зростання кінцевої суми боргу за простим і |
|
||||
складним відсотком |
|
|
|||
Для особи, яка надає гроші в борг (кредитора) більш вигідною є схема простих відсотків, якщо позика короткотермінова. При позиках понад рік доцільним є використання складних відсотків, а якщо тривалість позики рівно рік, то принципової різниці не існує. В усіх вказаних випадках передбачається, що використовується річна відсоткова ставка і відсотки нараховуються один раз на рік в кінці періоду.
У випадку короткотермінових позик (до 1 року) в якості величини n приймають співвідношення тривалості позики в днях до кількості днів у році:
n |
T |
, |
(5.11) |
|
K |
||||
|
|
|
||
54 |
|
|
|
де Т – термін позики в днях (день надання позики та день повернення боргу вважається одним днем), К – календарна тривалість року.
При цьому розрахунки ведуться, як для точного (365 днів), так і для звичайного за тривалістю (360 днів) років. Розрізняють такі випадки:
1.Точні відсотки з точним числом днів позики: (позичаються: “365/365”);
2.Звичайні відсотки з точним числом днів позики: (позичаються: “365/360”);
3.Звичайні відсотки з наближеним числом днів позики: (позичаються: “360/360”).
Точні відсотки означають, що тривалість року приймається точно (365 або 366 днів), а звичайні – спираючись на наближену кількість днів у році – 360.
Всі три випадки дають різний результат і використовуються в різних країнах. Так, в США надають перевагу першому підходу, а звичайні відсотки поширені в Європі.
У проектному аналізі широкого використання має схема нарахування складних відсотків. На практиці виникає багато різних ситуацій, пов’язаних з проблемами модифікації базової формули до відповідної ситуації немає.
Часто період нарахування не збігається з оголошеною відсотковою ставкою. Наприклад, оголошується річна відсоткова ставка, а нарахування здійснюються частіше ніж раз на рік (щоквартально, щомісяця, щоденно). В такому випадку розрахунки здійснюють за відсотковою ставкою, що дорівнює пропорційній періоду нарахування долі вихідної відсоткової ставки:
|
|
j n m |
|
||
S P 1 |
|
|
|
, |
(5.12) |
|
|||||
|
|
m |
|
|
|
де j – оголошена річна відсоткова ставка; m – кількість нарахувань за рік; n – кількість років.
Зазначимо, що при використанні простих відсотків проблеми урахування частоти нарахувань не існує. Кінцева сума боргу не залежить від кількості нарахувань від кількості нарахувань відсотків протягом періоду. Тобто, нагромадження за простими відсотками за ставкою 10% раз на рік, дає той же результат, що і, поквартальне нарахування за ставкою 2,5%.
Можливість нараховувати відсотки частіше ніж раз на рік використовується для регулювання ефективності боргових операцій при розрахунках за складними відсотками. Зрозуміло, що чим частіше здійснюють нарахування, тим більша кінцева сума. Важливо усвідомлювати, що місячна відсоткова ставка в розмірі 1% не еквівалентна 12% річних. Для порівняння
55
результативності застосування різних схем нагромадження у фінансовій математиці існує поняття ефективної відсоткової ставки. Це та реальна відсоткова ставка, яка відображає дійсну зміну вартості боргу за рік, а оголошену ставку називають в такому випадку номінальною.
При розрахунках за складними відсотками цілком ймовірно, що термін позики не дорівнює цілій кількості років. Борг може бути наданий на 40 місяців, або на 5,5 року тощо. В таких випадках для встановлення нагромадженої суми використовують два підходи:
1)загальний – з базовою формулою нагромадження;
2)змішаний – з використанням простих і складних відсотків.
При змішаному нарахуванні n представляють, як суму цілої частини і дробової, а S визначається із залежності:
S P (1 i)a (1 b i) , |
(5.13) |
де а – ціла кількість років, b – дробова кількість років.
Розглянуті вище аспекти нарахування відсотків враховують і при дисконтуванні. В проектному аналізі процеси дисконтування мають визначальне значення. Їх економічний зміст полягає в наступному: майбутні доходи, що очікують від проекту, повинні бути оцінені з сьогоднішньої позиції. Тобто всі витрати та надходження за проектом мають бути приведені до одного моменту часу (як правило – початку реалізації проекту) і тільки тоді можуть порівнюватись між собою.
5.3. Номінальні та реальні відсоткові ставки. Під час оцінки проектів необхідно обрати один з методів приведення всіх грошових потоків до базового року. Якщо використовується метод дисконтування, то всі грошові потоки приводять у відповідність з першим (нульовим) роком. При застосуванні методу компаундування всі грошові потоки приводять до останнього n-го року.
При оцінці величини грошових потоків з урахуванням фактора часу найбільш поширеними проблемами є:
1)складність вибору відповідної відсоткової ставки;
2)непослідовність у користуванні показниками відсоткових ставок. Величина відсоткової ставки відображає вартість капіталу для інвестора,
наприклад рівень дохідності за облігаціями державної позики. Оскільки цінність грошей у реальному виразі може знижуватися протягом часу через інфляцію, у проектному аналізі використовують такі відсоткові ставки:
56
- реальна ставка відсотка (r) – ставка доходу на капітал без урахування інфляції.:
r |
|
1 |
i |
1. |
(5.14) |
|
1 |
t |
|||||
|
|
|
||||
У разі використання реальної ставки відсотка необхідно проводити розрахунок грошових потоків у постійних цінах, тобто нейтралізувати вплив інфляції;
- номінальна (теперішня) ставка відсотка (i) – ставка доходу з позицій інвестора на приватному ринку, яка включає інфляцію (t), і визначається підсумовуванням реальної ставки процента та величини темпу інфляції:
i = r + t, |
(5.15) |
де r – реальна ставка відсотка (дохідність інвестицій); t – темп інфляції.
Якщо інфляція має значні темпи, то розрахунок номінальної ставки
відсотка здійснюється за формулою складних відсотків: |
|
i = r + t + r · t, |
(5.16) |
де r · t – інфляційна премія.
Інфляційна премія – це премія за інфляційне очікування, яку інвестори додають до реального, вільного від ризиків рівня доходу (норми прибутку).
Якщо в аналізі проекту використовують лише реальні (постійні) ціни, то для визначення вартості капіталу не слід збільшувати на інфляцію річні виробничі експлуатаційні витрати і вигоди.
Аналітики при аналізі фінансової привабливості проекту, який реалізується при певному рівні інфляції, повинні враховувати деякі взаємозалежні показники: номінальна дохідність проекту, його реальна дохідність, ставка податку та рівень інфляції. Слід пам’ятати, що високоефективні проекти більш чутливі до інфляційних процесів, їх номінальна дохідність різко збільшується в умовах зростання інфляційних процесів, однак при зниженні розвитку інфляції швидкість падіння дохідності відбувається випереджаючими темпами.
Окремими інфляційними сценаріями передбачені три можливих варіанти співвідношення номінальної ставки відсотка з темпом інфляції:
1)r = t – нарощення реальної вартості коштів не відбувається внаслідок того, що приріст їх майбутньої вартості поглинає інфляція;
2)r > t – реальна майбутня вартість коштів збільшується, незважаючи на інфляцію;
57
3) r < t – реальна майбутня вартість коштів знижується, тобто процес інвестування є збитковим.
5.4. Причини зміни вартості грошей в часі. Серед основних причин,
чому гроші втрачають свою вартість, виділяють наступні: інфляція, ризик та схильність до ліквідності.
Інфляція – це процес, який характеризується підвищенням загального рівня цін в економіці країни та зниженням купівельної спроможності грошей.
Інфляція завжди пов’язана із загальним підвищенням цін у країні. Коли ростуть ціни, знижується вартість грошової одиниці. Іншими словами, купівельна спроможність грошей сьогодні вища, ніж буде завтра: через рік за одну грошову одиницю можна купити більше, ніж за ту саму одиницю через два роки. Інфляція проявляється у переповненні сфери обігу товарів грошима внаслідок їх надмірного випуску або у скороченні товарної маси в обігу при незмінній кількості випущених грошей. Головними чинниками інфляційних процесів також є помилки в політиці ціноутворення.
Ризик – це нестабільність, невпевненість у майбутньому.
Через непевність у майбутньому ризик з часом зростає, люди хочуть уникнути ризику, тож вище оцінюють ті гроші, що є сьогодні, ніж ті, що будуть
вмайбутньому. Через певні побоювання в майбутньому ризик з часом зростає. Більшість людей прагне уникнути ризику, вони готові віддати свої гроші тепер
вобмін на гроші в майбутньому, але тільки за відповідну компенсацію. Неможливо точно передбачити чи повернути гроші, вкладені в проект.
Немає жодної гарантії, що якась фінасово міцна компанія буде такою завжди. Інвестори не можуть бути впевнені, що отримають дивіденди і, що ціна акцій не впаде. Немає певності в тому, що проценти і основа боргу за цінними паперами з фіксованим доходом будуть виплачені, як пообіцяла компанія, що випустила ці папери. Фінансові аналітики, досвідчені інвестори, незалежно від їхньої компетентності, не можуть твердо гарантувати, що доходи, які вони передбачають, будуть саме такими, як планувалось. Як непевність зростає відповідно до тривалості прогнозованого періоду, так само зростає і ризик. Відповідно зменшується сподівана вартість грошей.
Ліквідність – це можливість швидкого переводу активу у готівку без істотної втрати його вартості (з мінімальними втратами).
Активи – це ресурси фірми, що нараховані як її власність, або підтвердження боргових зобов’язань.
Тобто це усе чим володіє підприємство (готівка, дебіторська заборгованість, обладнання та майно підприємства).
58
Схильність до ліквідності – це перевага, надана наявним грошам переді іншими цінностями та ризикованими вкладеннями.
Коли населення вкладає свої гроші, сподіваючись на майбутні надходження, вони очікують високої винагороди як компенсації за втрату ліквідності, що впливає на цінність грошей в часі. Ліквідність залежить від спроможності реалізувати активи компанії, щоб одержати гроші. Інвестори схильні до ліквідності, а тому про всякий випадок віддають перевагу наявним грошам замість того, щоб вкладати їх у проекти, сподіваючись на майбутні доходи. Якщо вони здійснюють інвестування, то міняють гарантовані «живі» гроші на ризиковані доходи в майбутньому. Цей “обмін” можливий лише за умови: майбутні доходи будуть досить високі, аби виправдати ризик, який беруть на себе інвестори. Коли кредитори чи інвестори вкладають свої гроші, сподіваючись на майбутні надходження, вони сподіваються на високу винагороду, як компенсацію за втрату ліквідності. І навпаки, якщо гроші вкладаються у не ризиковані проекти, сподівані доходи досить низькі.
При визначенні ставки дисконту орієнтуються на процентну ставку кредитних організацій і ставку дохідності. Дисконтну ставку визначають як рівень дохідності, що можна отримати виходячи з різних інвестиційних можливостей. У фінансовому аналізі ставку дисконту, як правило, визначають на базі того процента, під який дана фірма може позичити кошти.
Розмір процентної ставки інвестицій базується, в основному, на рівні віддачі, яку ці вкладення можуть принести інвесторам, а сама ставка визначається цілями та напрямами інвестицій.
Розмір премії за ризик встановлюється експертним шляхом. Для визначення орієнтованої величини премії для ризикових операцій з процентами можна скористатися рекомендаціями зарубіжних експертів (табл. 5.1).
Таблиця 5.1
Види інвестицій і відповідний розмір процентної ставки
Види інвестицій |
|
|
|
Відсоткова |
|
|
|
|
ставка |
||
|
|
|
|
|
|
|
|
|
|
|
|
Вимушені |
|
|
|
|
Вимоги до норми |
|
|
|
|
прибутку відсутні |
|
|
|
|
|
|
|
|
|
|
|||
Вкладення з метою збереження позицій на ринку |
|
близько 6 % |
|||
|
|
|
|||
Оновлення основних виробничих фондів |
|
10-15 % |
|||
|
|
|
|
|
|
Вкладення |
з метою |
зниження |
виробничих |
витрат |
від 15 % |
завдяки використанню нової технології |
|
||||
|
|
||||
|
|
||||
Вкладення з метою освоєння нового ринкового сегмента |
від 20 % |
||||
|
|
|
|
|
|
Ризикові |
інвестиції, |
пов’язані |
з випуском |
нової |
від 25 % |
продукції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
59 |
|
|
Питання для самоконтролю
1. Які причини зміни вартості грошей у часі Ви знаєте? 2. Що таке майбутня та теперішня вартість грошей?
3. Що таке ставка відсотка?
4. Що таке реальна та номінальна відсоткова ставка?
Лекція 6 Грошові потоки та їх використання у проектному аналізі
1.Поняття грошового потоку
2.Види грошових потоків
3.Проектний грошовий потік та його розрахунок
4.Принципи управління грошовими потоками
6.1. Поняття грошового потоку. Вітчизняна практика оцінки інвестиційних рішень довгий час базувалася на визначенні величини прибутку, яку можна отримати в результаті реалізації проекту. Однак було б помилкою оцінювати проекти за критерієм чистого доходу, а не грошового потоку (cash flow). Використання грошового потоку дозволяє враховувати подію, яка об’єктивно відбулася – отримання або сплата грошей. Трактування деяких грошових витрат з точки зору бухгалтерського обліку не впливає на розмір прибутку і терміни його виявлення. Іноді вагомі грошові надходження не впливають на розмір доходу, і навпаки.
Під грошовим потоком розуміють різницю між кількістю отриманих і витрачених грошей, фактичні чисті готівкові кошти, які надходять у фірму (чи витрачаються нею) протягом деякого визначеного періоду.
З точки зору проектного аналізу, грошовий потік обчислюється як різниця між надходженнями грошових коштів та їх витратами, що виникають у результаті реалізації проекту.
Значення грошового потоку характеризується:
-припливом, що дорівнює розміру грошових надходжень (чи результатом
угрошовому виразі);
-відпливом, що дорівнює витратам (платежам);
-сальдо, що дорівнює різниці між припливом і відпливом.
Баланс підприємства – це звіт про фінансовий стан підприємства, який відображає на певну дату його активи, зобов'язання і власний капітал.
60
