7.2. Основні види задач нелінійного програмування

Для розв’язування задач нелінійного програмування не існує універсального методу, а тому доводиться застосовувати багато методів та обчислювальних алгоритмів, які в основному ґрунтуються на теорії диференціального числення, і вибір їх залежить від конкретної постановки задачі та форми економіко-математичної моделі.

Методи нелінійного програмування бувають прямі та непрямі. Прямими методами оптимальні розв’язки шукають у напрямку найшвидшого збільшення (зменшення) цільової функції. Типовими для цієї групи методів є градієнтні. Непрямі методи полягають у зведенні задачі до такої, знаходження оптимального розв’язку якої вдається спростити. Найпоширенішими методами цього класу є методи квадратичного програмування.

Оптимізаційні задачі, на змінні яких накладаються обмеження, розв’язуються методами класичної математики. Оптимізацію з обмеженнями-рівностями виконують методами зведеного градієнта, наприклад, методом множників Лагранжа. У задачах оптимізації з обмеженнями-нерівностями досліджують необхідні та достатні умови існування екстремуму Куна-Таккера.

Розглянемо метод множників Лагранжа на прикладі такої задачі нелінійного програмування:

Z = f(x₁,x₂,...,x_n) max(min), (7.3)

, (7.4)

де f(x₁,x₂,...,x_n) та - диференційовані.

Ідея методу Лагранжа полягає в заміні окресленої задачі простішою - знаходження екстремуму складнішої функції, але без обмежень. Ця функція називається функцією Лагранжа і записується у вигляді:

(7.5)

де - невизначені поки що величини, так звані множники Лагранжа.

Необхідною умовою екстремуму функції багатьох змінних є рівність нулю частинних похідних стосовно всіх змінних функції. Візьмемо ці частинні похідні і прирівняємо їх до нуля:

Отримуємо систему (m+n) рівнянь із (т+n) невідомими, розв’язавши яку, знайдемо та - стаціонарні точки. Оскільки їх знайдено з необхідної умови екстремуму, то в них можливий максимум або мінімум. Іноді стаціонарна точка є сідловою (точкою перегину графіка функції).

Теорема. Нехай в околі критичної точки функція має неперервні частинні похідні до другого порядку включно. Розглянемо вираз

1) Якщо > 0, то в точці функція має такі екстремуми:

а) досягає свого максимального значення, якщо < 0;

б) досягає свого мінімального значення, якщо > 0;

2) Якщо < 0, то в точці функція не має екстремумів.

3) Якщо =0, то в точці для функції

екстремуми можуть існувати чи не існувати.

Розглянемо задачі випуклого програмування, які є структурними складовими класу задач нелінійного програмування, в яких використовують опуклі чи вгнуті функції. Функція f(x₁,x₂,...,x_n), яка визначена на опуклій множині М, називається опуклою, якщо для будь-яких двох точок х1 і х₂ з множини М і довільної константи з проміжку [0; 1], () справджується співвідношення:

Функція f(x_l,x₂,...,x_n), яка визначена на опуклій множині М, називається увігнутою, якщо для будь-яких двох точок х1 і х₂ з множини М і довільної константи з проміжку [0; 1], () справджується співвідношення

Розглянемо задачу опуклого програмування.

Z = f(x₁,x₂,...,x_n) max(min), (7.6)

,(7.7)

, (7.8)

де f(x₁,x₂,...,x_n) - увігнута (опукла) функція; - опуклі функції.

Множина допустимих рішень задачі (7.6)-(7.8) задовольняє умову регулярності, якщо існує хоч би одна точка X = (х₁,х₂,...,х_п) в описуваній множині з координатами, що задовольняють нерівності ,.

Якщо f(x_ux₂,...,x_n) - увігнута (опукла) функція, яка задана на опуклій множині, то будь-який локальний максимум (мінімум) є глобальним максимумом (мінімумом).

Функція Лагранжа для задачі опуклого програмування записується в такому ж вигляді, як і для будь-якої задачі нелінійного програмування

де - множники Лагранжа.

Точка називається сідловоюточкою функції Лагранжа, якщо

для всіх , ,.

Теорема (теорема Куна-Таккера). Якщо множина допустимих розв’язків задачі опуклого програмування (7.6)-(7.8) задовольняє умову регулятивності, то точка буде оптимальнимрозв’язком задачі тільки тоді, коли існує такий вектор , , що - сідлова точка функції Лагранжа.

Теорема Куна-Таккера дає можливість сформулювати математичні вирази, що визначають необхідні та достатні умови наявності сідлової точки. Це відображає така теорема.

Теорема. Якщо задачу нелінійного програмування

Z = f(x₁,x₂,...,x_n) max,,

;

,

де Z = f(x₁,x₂,...,x_n) та , - неперервно диференційовані по х функції, то для того, щоб вектор був оптимальним розв’язком задачі, необхідно щоб існував такий вектор , що точка з координатами була би сідловою точкою функції Лагранжа, тобто щоб виконувалися умови:

та - значення відповідних похідних функції Лагранжа, обчислені в сідловій точці.

Розглянемо задачі квадратичного програмування, які є частковим випадком задач опуклого програмування, в яких цільова функція є сумою лінійної та квадратичної форми. Квадратичною формою відносно змінних є числовафункція цих змінних вигляду:

Квадратична форма називається додатно (від’ємно) визначеною, якщо Z(X)>0 (Z(X)<0) для всіх значень змінних Х = (х₁,х₂,...,х_п), крім Х=0.

Квадратична форма Z(X) називається напіввизначеною, якщо Z(X)>0 (Z(X)<0) для всіх значень змінних X = (х₁,х₂,...,х_п), крім цього існує такий вектор , не всі координати якого рівні нулю і для якого Z(X ) = 0.

Квадратична форма Z(X) називається неозначеною, якщо її значення є додатними для одних значень Х і від’ємними для інших.

Вид квадратичної форми можна визначити через власні значення (характеристичні корені) матриці коефіцієнтів С, де

Складаємо характеристичне рівняння матриці С.

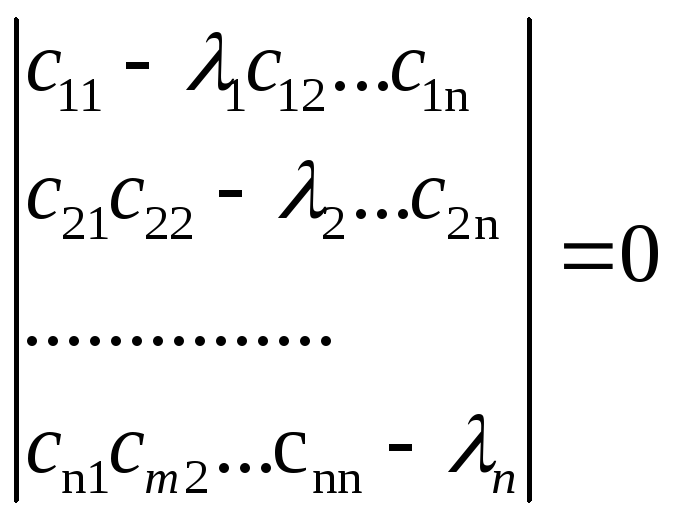
3 цього рівняння визначаємо вектор характеристичних коренів:

.

Теорема. Квадратична форма є додатно (від’ємно) визначеною тільки тоді, коли всі компоненти вектора характеристичних коренів є додатними (від’ємними).

Якщо власні числа мають різні знаки, то квадратична форма є невизначеною.

Задача квадратичного програмування - це задача виду

при обмеженнях

,

де - додатно (від’ємно) визначена квадратична форма.

Умови Куна-Таккера для задачі випуклого програмування мають вигляд:

Теорема. є оптимальным розв’язком задачі квадратичного програмування тільки тоді, коли існують такі m-вимірні вектори n-вимірний вектор V>0, для яких виконуються умови:

I.

II.

III.

IV.

7.3. Прикладне використання методу множників Лагранжа

Розглянемо економічний зміст множників Лагранжа. Для цього розглянемо задачу нелінійного програмування стосовно визначення оптимального плану виробництва продукції при обмежених ресурсах:

.

Головною метою виробництва продукції є отримання найбільшого прибутку від реалізації, тому цільовою функцією Z задачі є прибуток від реалізації продукції обсягом одиниць. Зауважимо, що функція - нелінійна.

Для виробництва продукції використовується т видів сировини, обсяги запасів яких обмежені і становлять () одиниць. Запишемо систему нерівностей

() у вигляді

().

Тобто, якщо - обсяг сировини і-гo виду, що використовується для виробництва всієї продукції, то - залишок цього ресурсу після її виробництва. Якщо , то сировина використана повністю; якщо , то на виробництво продукції використана не вся сировина; якщо , то наявної сировини не вистачає для виробництва продукції.

Розглянемо функцію Лагранжа для описуваної задачі:

Очевидно, що , тобто ця похідна показує, як змінюється значення цільової функції залежно від обмежень. Множники Лагранжа є двоїстими змінними задачі про використання ресурсів. Вони можуть бути ціною, за якою на ринку продається чи купується одиниця і-го виду сировини. Якщо і , то можна продати залишки сировини і отримати додатковий прибуток в розмірі . Якщо ж , то можна купити потрібну кількість, витративши грошових одиниць і забезпечити виробництво продукції обсягом . Функцію Лагранжа можна трактувати як загальний прибуток від виробництва, який містить прибуток від реалізації виготовленої продукції f(x) та прибуток від продажу залишків сировини (або витрати на придбання потрібної т кількості сировини) .