7. Теорема Остроградського – Гаусса для магнітного поля у вакуумі

Магнітним потоком (потоком вектора магнітної індукції)через малу ділянку поверхні, проведеної в полі, називають фізичну величину:

, (5.40)

де − вектор магнітної індукції в точках малої ділянки поверхні площею,− одиничний вектор нормалі до площинки, а вектор,− проекція векторана напрям нормалі. Мала ділянка поверхні має бути такою малою, щоб в її межах можна було знехтувати неоднорідністю поля і кривиною поверхні.

Магнітний потік через довільну поверхню S:

. (5.41)

При цьому всі вектори нормалей до малих площинокмають бути напрямлені в один і той самий бік відносно поверхніS. Наприклад, у разі замкненої поверхні S всюди далі під слід розуміти вектори зовнішніх нормалей, тобто напрямлені назовні з області, обмеженої цією поверхнею.

Якщо магнітне поле однорідне, а поверхня S плоска, то

.

Теорема Остроградського – Гаусса для магнітного поля:

Магнітний потік через довільну замкнену поверхню S дорівнює нулеві.

. (5.42)

Цей результат є математичним виразом того, що у природі немає магнітних „зарядів”, подібних до електричних – джерел магнітного поля. Згідно з термінологією, яка прийнята у векторному аналізі, теорема Остроградського – Гаусса стверджує те, що магнітне поле являє собою поле, яке називають соленоїдним.

8. Робота переміщення провідника зі струмом у постійному магнітному полі

Якщо провідник рухається в постійному за часом магнітному полі, то елементарна робота , що виконується силою Амперапри малому переміщеннімалого елементапровідника зі струмом, дорівнює

,

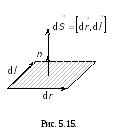
де 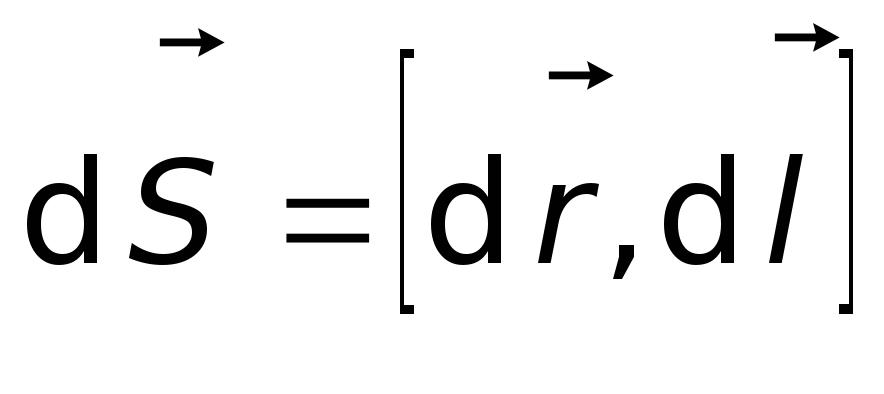− вектор малої площинки, яку прокреслює елементпровідника при його малому переміщенні(рис. 5.15), а− магнітний потік через цю площинку.

При малому переміщенні в магнітному полі провідника скінченної довжини зі струмом

, (5.43)

де − магнітний потік через поверхню, яку прокреслює весь провідник при його малому переміщенні, тобто

.

Якщо провідник, в якому , здійснює скінченне переміщення в магнітному полі зі стану1 у стан 2, то робота сил Ампера на цьому переміщенні

, (5.44)

де − магнітний потік через поверхню, що прокреслив провідник при розглядуваному переміщенні.

9. Рух заряджених частинок у постійному магнітному полі

Якщо на рухому частинку з електричним зарядом водночас діють і електричне, і магнітне поле, то сила, що діє на заряджену частинку, тобто сила Лоренца, згідно з (5.4), дорівнюватиме:

,

де − напруженість електричного поля,− магнітна індукція,− швидкість частинки.

Розгляньмо рух заряджених частинок в однорідному магнітному полі. При цьому вважатимемо, що на частинки не діють ніякі електричні поля, тобто сила Лоренца має тільки магнітну складову:

.

Сила напрямлена перпендикулярно до швидкостізарядженої частинки і визначає нормальне прискорення частинки. Оскільки силаперпендикулярна швидкості, то вона роботи не виконує. Кінетична енергія частинки, а отже, і модуль її швидкості лишаються незмінними. Силазалежить від швидкості частинки і від індукції поля. Те й інше не змінюються. Тому лишається незмінним модуль сили

.

Якщо частинка влітає в однорідне магнітне поле так, що її швидкість напрямлена вздовж лінії магнітної індукції (кут міжідорівнює нулеві або), то. Частинка продовжуватиме рухатися в магнітному полі рівномірно і прямолінійно.

Якщо ж кут , тобто частинка влітає в магнітне поле в напрямі, перпендикулярному лініям магнітної індукції, то на неї діє сила Лоренца, модуль якої

. (5.45)

Під дією цієї сили траєкторія частинки викривляється. Незмінність нормального прискорення означає, що радіус кривини плоскої траєкторії частинки сталий. Частинка рівномірно рухається в однорідному полі вздовж дуги кола, площина якого перпендикулярна лініям індукції. Згідно з другим законом Ньютона

,

де − маса частинки,− радіус кола.

Звідси дістанемо радіус кола:

. (5.46)

Якщо частинка релятивістська,

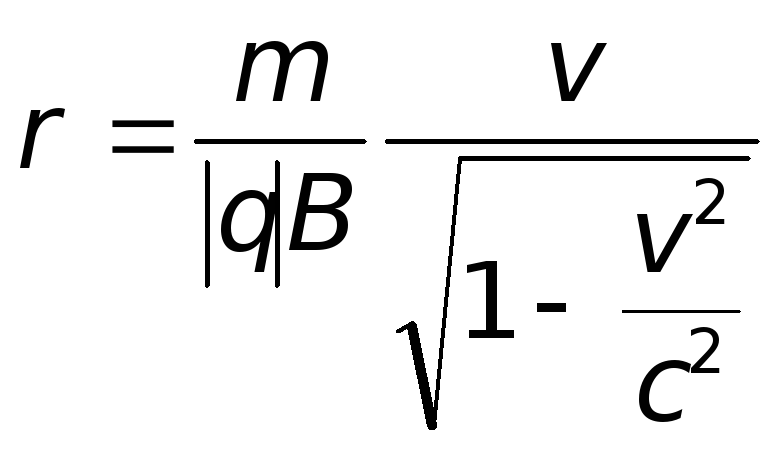, (5.47)

де − швидкість світла у вакуумі.

Розгляньмо загальний випадок руху зарядженої частинки в однорідному магнітному полі, коли її швидкість напрямлена під довільним гострим кутомдо вектора магнітної індукції(рис. 5.16). Нехай частинкою буде електрон. У площиніxOz, перпендикулярній лініям індукції, електрон рухатиметься вздовж кола із швидкістю, що дорівнює . Водночас він рухатиметься і вздовж поля зі швидкістю. Внаслідок одночасної участі в рухах вздовж кола і вздовж прямої електрон рухатиметься вздовж гвинтової лінії. Радіус кола згідно з (5.46):

, (5.48)

де – заряд електрона,− його маса. Крок гвинтової лінії дорівнює шляхові, який проходить електрон уздовж поля (осіу) зі швидкістю за проміжок часу, що потрібний електрону для того, щоб здійснити один оберт,

, (5.49)

де − період обертання електрона. Підставивши цей вираз дляТ у формулу (5.49), дістанемо крок гвинтової лінії:

. (5.50)