10.2 Энтропия равномерного закона распределения

Энтропия равномерного закона распределения. Для равномерного распределения W(x)=1/(b-a). По формуле для дифференциальной энтропии получаем

С увеличением интервала (b-a) значение h(X) также увеличивается.

10.3 Энтропия гауссового закона распределения.

Энтропия гауссового закона распределения. Найдем плотность вероятности стационарного случайного процесса X(t), с ограниченной средней мощностью, которая обеспечивает максимум h(X). другими словами, необходимо найти махсимум функции в следующей постановке: задан целевой функционал:

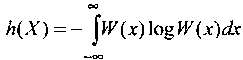
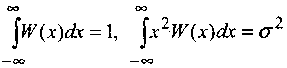и ограничения

Найти такую W(x), которая доставляет максимум энтропии h(X).

Решение этой задачи известно, и приводит к тому, что искомая плотность вероятности, удовлетворяющая условиям максимизации является гауссовой функцией

а максимальная энтропия

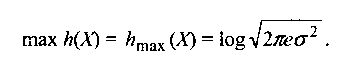
Следовательно, среди всех источников случайного сигнала с ограниченной и одинаковой средней мощностью (дисперсией) наибольшей энтропией владеет источник с гауссовским распределением сигнала.

На практике мы всегда имеем дело с сигналами (сообщениями и помехами) конечной длины и конечной энергии. При этом если продолжительность сигнала T_s, а его ширина спектра ∆f, то без потери информации такое непрерывное сообшение может быть представлено N=T_s*2∆f независимыми отсчетами . Таким образом для гаусового распределения энтропия отрезка непрерывного сообщения длительностью T_s будет равна

Лекция 11

11.1 Пропускная способность канала связи с помехами для непрерывных сообщений

Рассмотрим канал связи с аддитивним гауссовим шумом n(t), на вход которого поступает информация в виде непрерывного сигнала S(t). Выход такого канала является случайным процессом y(t), каждая реализация которого может быть представлена в виде

y(t) = S(t) + n(t).

Скорость передачи непрерывных сигналов (сообщений) определим, как разницу соответствующих производительностей выхода канала и шума в канале:

R=V*[h(y)-h(n)]

где V=1/T_s - скорость передачи сообщения в канале, которая определяется временем передачи сигнала длительностью T_s , а h(y) и h(n) -дифференциальная энтропия выхода канала и шума в канале соответственно.

Пусть эффективная полоса пропускания канала, что выбрана в соответствии с максимальной шириной спектра сигнала F_max , равняется ∆f и время передачи сигнала равно T_{s .} В этом случае производительность шума

R_n(n)=V*h(n), и

где Рш -мощность шума в полосе ∆f

Пропускная способность канала связи по определению равняется

(*)

где максимум отыскивается по всем законами распределения W(y) - плотности вероятности процесса

y(t) = S(t) + n(t)

на выходе канала связи (на входе приемника).

Найдем пропускную способность канала связи при условии, что средняя мощность сигнала ограничена, а помехой в канале является белый нормальный шум.

Как и раньше, будем считать, что все потери информации происходят только за счет шума. В этом случае максимизация пропускной способности расписанной выше, сводится к такому формированию сигнала S(t), чтобы процесс на выходе канала связи y(t)= S{t) + n(t) имел нормальное распределение, поскольку такой сигнал имеет максимальную энтропию. Это чрезвычайно важный вопрос рассмотрим более подробно.

Из статистики хорошо известно, что процесс y(t) = S(t) + n(t) имеет нормальное распределение при условии, что шум n(t) распределен нормально, по крайней мере в двух случаях. Во первых, если S(t) - детерминированная функция. Однако в этом случае вероятность реализации p[S(t)]=1, и следовательно, реализация S(t) не несет получателю никакой информации,

Второй случай, когда S(t) гаусовский процесс. Здесь действует правило композиции гауссових законов : при сложении двух гауссовских процессов результирующий процесс является также гауссовским, причем математические ожидания и дисперсии суммируются.

Поскольку сигнал S(t) и шум n(t) независимые, то средняя мощность суммарного колебания y(t) определяется суммой их мощностей : P_y = Ps + Р_ш.

Поскольку шум имеет гауссовское распределение, то для того, чтобы суммарный сигнал имел максимальную энтропию, необходимо, чтобы информационный или полезный сигнал также имел гауссовое распределение. В этом случае производительность R_y суммарного колебания

y(t) = S(t) + n(t).

которое представляет случайный процесс на входе приемника, максимальна и равняется

(**)

Таким образом, на основании выражений (*) и (**) пропускная способность гауссового канала связи определяется соотношением:

бит/c (***)

Выражение (***) представляет широко известную в теории связи формулу Шеннона для пропускной способности непрерывного канала с гауссовою помехой. Эта формула связывает ширину спектра сигнала и отношения сигнал/шум на выходе канала связи (или на входе приемника) с пропускной способностью непрерывного канала. Из нее следует, что одну и ту же пропускную способность можно получить при разнообразных соотношениях пар ∆f и Ps/Pш, то есть существует возможность своеобразного размена между полосой пропускания и отношением сигнал/ шум для достижения заданной пропускной способности канала.

Из формулы Шеннона вытекает также, что увеличить пропускную способность можно за счет расширения полосы пропускания канала, который выбирается в соответствии с шириной спектра сигнала. Отсюда появляется задача синтеза шумоподобных импульсных сигналов с максимальной шириной спектра для переноса максимальгого количества информации. Эти выводы являются своеобразным мостиком между теорией информации и теорией кодирования сигналов.

Рассмотрим предельные характеристики пропускной способности при изменении ∆f . Учитывая, что Pш=N₀*∆f , где N₀ - спектральная плотность мощности белого шума, выражение для пропускной способности приобретает вид:

C=∆f log₂(1+Ps/N₀∆f )

откуда видно, что С монотонно зависит от ∆f .

Для нахождения максимума этой функции достаточно найти предел

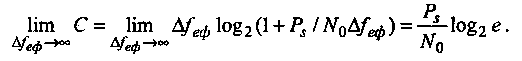
Соотношение представляет предельное (максимально возможно) значение пропускной способности канала при заданном отношении Ps / N₀ на входе приемника.

Обозначим

Проведем нормирование пропускной способности канала к величине h₀²

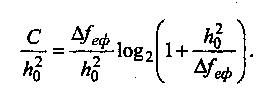
График зависимости нормируемой пропускной способности от отношения ∆f / h₀² имеет вид:

Из анализа графика вытекает, что пропускная способность канала быстро растет при расширении полосы пропускания канала только на начальном участке кривой, где мощность сигнала больше мощности шума.

Отметим, что, как показывают исследования, скорость передачи во многих существующих системах связи еще слишком далека от теоретически возможных значений пропускной способности.