7.3 Построение образующей(порождающей) матрицы |om|.
Линейные коды обладают следующим свойством:
- из всего множества 2k разрешенных кодовых слов, образующих линейную группу, можно выделить подмножества из k слов, обладающих свойством линейной независимости.
Линейная независимость означает, что никакое из слов, входящих в подмножество линейно-независимых кодовых слов, нельзя получить путем суммирования (с помощью линейного выражения) любых других слов, входящих в это подмножество.
В то же время любое из разрешенных кодовых слов можно получить путем суммирования определенных линейно-независимых слов.
Таким образом, построение кодовых комбинаций линейного кода связано с линейными операциями. Для выполнения таких операций удобно пользоваться хорошо разработанным аппаратом матричных вычислений.
Для образования n -разрядных кодовых слов из k- разрядных кодируемых слов (кодирования) используют матрицу, которая называется образующей(порождающей).
Образующая матрица получается путем записи в столбец k линейно-независимых слов.
Обозначим кодируемую информационную последовательность X и будем записывать ее в виде матрицы-строки ||X|| размерностью 1*k, например:
||X||=||11001||, где k=5.
Один из способов построения образующей (порождающей) матрицы следующий: Она строится из единичной матрицы ||I|| размерностью k*k и приписанной к ней справа матрицы добавочных (избыточных) разрядов ||МДР|| размерности k*r.
где при k=4
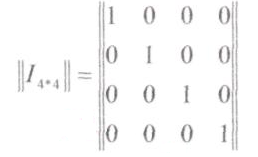
Такая структура ОМ обеспечивает получение систематического кода.
Порядок построения матрицы МДР будет рассмотрен ниже.
7.4 Порядок кодирования
Кодовое слово КС получается путем умножения матрицы информационной последовательности ||Х|| на образующую матрицу ||ОМ||:
Умножение выполняется по правилам матричного умножения: (ТАК наТАК)
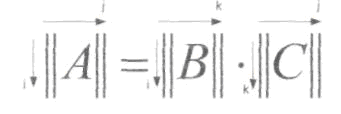
Надо только помнить, что сложение здесь ведется по модулю 2.
Пример:
допустим, образующая матрица
1000 110
0100 111
||ОМ||= 0010 011
0001 101
и вектор-строка информационной последовательности
Так как множимая матрица имеет всего одну строку, умножение упрощается. В этом случае следует поставить в соответствие строкам образующей(порождающей) матрицы ||ОМ|| разряды матрицы информационной последовательности ||X|| и сложить те строки образующей(порождающей) матрицы, которые соответствуют единичным разрядам матрицы ||Х||.
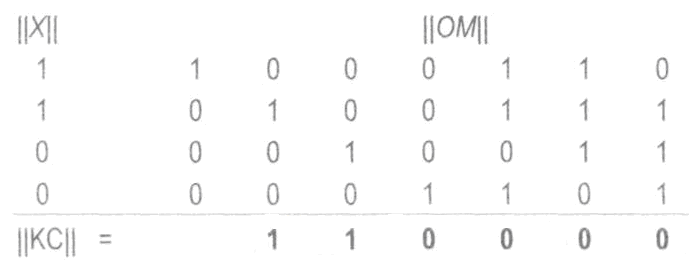
Заметим, что ||KC|| = ||X, ДР||,
где ||X||- информационная последовательность (т.к. умножается на единичную матрицу ||I||),
а ||ДР|| - добавочные разряды, зависящие от матрицы добавочных разрядов ||МДР||:
|| ДР ||= || Х || * || МДР||
7.5 Порядок декодирования
В результате передачи кодового слова через канал оно может быть искажено помехой. Это приведет к тому, что принятое кодовое слово ||ПКС|| может не совпасть с исходным ||КС||.
Искажение можно описать с помощью следующей формулы:
|| ПКС || = ||КС || + ||ВО ||,
где ||ВО|| - вектор ошибки - матрица-строка размерностью 1*n, с 1 в тех позициях, в которых произошли искажения.
Декодирование основано на нахождении так называемого опознавателя или синдрома ошибки -матрицы-строки ||ОП|| длиной r разрядов (r- количество добавочных или избыточных разрядов в кодовом слове).
Опознаватель используется для нахождения предполагаемого вектора ошибки.
Опознаватель находят по следующей формуле:
||ОП|| = ||ПКС||* ||ТПМ||,
где ||ПКС||- принятое и, возможно, искаженное кодовое слово;
||ТПМ||,- транспонированная проверочная матрица, которая получается из матрицы добавочных разрядов ||МДР|| путем приписывания к ней снизу единичной матрицы:
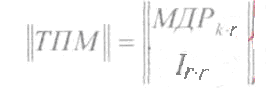
Пример ||ТПМ||:
Поскольку ||ПКС|| = ||КС|| + ||BO||, последнюю формулу можно записать в виде:
||ОП|| = ||КС|| * ||ТПМ||+||ВО|| * ||ТПМ||.
Рассмотрим первое слагаемое.
||КC|| - матрица-строка, причем первые k разрядов - информационные.
Докажем теперь, что произведение кодового слова ||КС|| на ||ТПМ|| приводит к получению нулевой матрицы ||0||.
Поскольку ||КС|| - матрица-строка, возможен упрощенный порядок умножения матриц, рассмотренных выше.
Следовательно, первое слагаемое в
||ОП|| = ||КС|| * ||ТПМ|| + ||ВО|| * ||ТПМ||
всегда равно нулю и опознаватель полностью зависит от вектора ошибки ||ВО||.
Если теперь подобрать такую проверочную матрицу ТПМ, а значит и МДР, чтобы разным векторам ошибки соответствовали разные опознаватели ОП, то по этим опознавателям можно будет находить вектор ошибки ВО, а значит и исправлять эти ошибки.
Соответствие опознавателей векторам ошибки находится заранее путем перемножения векторов исправляемых ошибок на ТПМ;
Таким ооразом, способность кода исправлять ошибки целиком определяется ||МДР||. Для построения МДР для кодов, исправляющих однократные ошибки нужно в каждой строке МДР иметь не менее 2-х единиц. При этом также необходимо иметь хотя бы одно различие между двумя любыми строчками МДР.
Полученный нами код неудобен тем, что опознаватель, хотя и связан однозначно с номером искаженного разряда, как число не равен ему. Для поиска искаженного разряда нужно использовать дополнительную таблицу соответствия между опознавателем и этим номером. Коды, в которых опознаватель как число определяет позицию искаженного разряда, были найдены и получили название кодов Хэмминга.
Построение МДР для случая исправления многократных ошибок значительно усложняется. Разными авторами были найдены различные алгоритмы построения ||МДР || для этого случая, а соответствующие коды называются именами их авторов.