Длина дуги меридиана от экватора до точки

Длина дуги (Х) меридиана от экватора (В=0⁰) до точки (или до параллели) с широтой (В) вычисляется по формуле:

(4.1)

где

Задание 4.2 Вычислить длины дуг меридиана от экватора до точек с широтами B₁ = 31°00' (широта нижней рамки трапеции) и B₂ = 31°20' (широта верхней рамки трапеции).

Для рассматриваемого примера имеем:

Х_o^B1 = 3431035,2629

Х_o^B2 = 3467993,3550

Для контроля длины дуг меридиана от экватора до точек с широтами B₁, и B₂ можно также вычислить по формуле:

(4.2)

где:

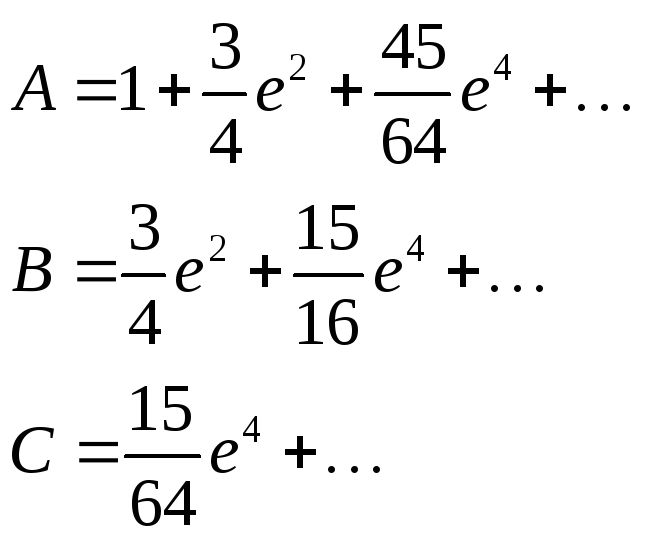
Для рассматриваемого примера имеем:

Х_o^B1 = 3431035,2689

Х_o^B2 = 3467993,3605

Лабораторная работа № 5 Вычисление размеров съёмочной трапеции.

Длина дуги (ΔX) меридиана между параллелями с широтами В₁ и В₂ вычисляется по формуле:

(5.1)

где ΔB=В₂-В₁ – приращение широты (в угловых секундах);

- средняя широта; ρ” = 206264,8” – количество секунд в радиане; М₁, М₂ и М_m – радиусы кривизны меридиана в точках с широтами В₁, В₂ и В_m.

Задание 5.1 Вычислить радиусы кривизны меридиана, первого вертикала и средний радиус кривизны для точек с широтами B₁ = 31°00' (широта нижней рамки трапеции), B₂ = 31°20' (широта верхней рамки трапеции) и и B_m,= (B₁ + B₂)/2 (средняя широта трапеции)

Для рассматриваемого примера имеем:

В1 =	31° 00'	M1 =	6352463,644	N1 =	6383914,9	R1 =	6368169,865
В2 =	31° 20'	M2 =	6352792,871	N2 =	6384025,2	R2 =	6368389,890
Вm =	31° 10'	Mm =	6352628,003	Nm =	6383970,0	Rm =	6368279,708

Задание 5.2 Вычислить длину дуги меридиана между точками с широтами B₁ = 31°00' (широта нижней рамки трапеции), B₂ = 31°20' (широта верхней рамки трапеции) на местности и на карте масштаба 1 : 100 000 .

Решение.

Вычисление длины дуги меридиана между точками с геодезическими широтами B₁, и B₂ по формуле 5.1даёт результат на местности:

ΔХ = 36958,092 м.,

на карте масштаба 1:100 000 :

ΔХ = 36958,09210м. : 100000 = 0,3695809210м. ≈ 369,58мм.

Для контроля длину дуги меридиана ΔХ между точками с геодезическими широтами B₁, и B₂ можно вычислить по формуле:

ΔХ = Х_o ^B2 –Х_o ^B1 (5.2)

где Х₀^В1 и Х₀^В2 - длины дуги меридиана от экватора до параллелей с широтами В₁ и В₂ что даёт результат на местности:

ΔХ = 3467993,3550 – 3431035,2629 = 36958,0921м.,

на карте масштаба 1:100000 :

ΔХ = 36957,6715 м.м. : 100000 = 0,369575715м. ≈ 369,58мм.

Длина дуги параллели

Длина дуги параллели вычисляется по формуле:

(5.3)

где N – радиус кривизны первого вертикала в точке с широтой В;

ΔL=L₂ - L₁ – разность долгот двух меридианов (в угловых секундах);

ρ” = 206264,8” – количество секунд в радиане.

Задание 5.3 Вычислить длины дуг параллелей на геодезических широтах B₁=31°00' и B₂=31°20' между меридианами с долготами L₁=66°00' и L₂=66°30'.

Решение.

Вычисление длины дуги параллели на геодезических широтах B₁, и B₂ между точками с долготами L₁' и L₂ по формуле 5.3 даёт результат на местности:

ΔУ_Н = 47 752,934 м., ΔУ_В = 47 586,020 м.

на карте масштаба 1:100 000 :

ΔУ_Н = 47 752,934м. : 100000 = 0, 47752934 м. ≈ 477,53мм.

ΔУ_В = 47 586,020м. : 100000 = 0, 47586020м м. ≈ 475,86мм.

Вычисление площади съемочной трапеции.

Площадь съемочной трапеции вычисляется по формуле:

(5.4)

Задание 5.4 Вычислить площадь съёмочной трапеции ограниченной параллелями с широтами B₁=31°00' и B₂=31°20' и меридианами с долготами L₁=66°00' и L₂=66°30'.

Решение

Вычисление площади съёмочной трапеции по формуле 5.4 даёт результат:

Р = 1761777864,9 м². = 176177,7865 га. = 1761,778 км².

Для грубого контроля площадь съемочной трапеции можно вычислить по приближённой формуле:

(5.5)

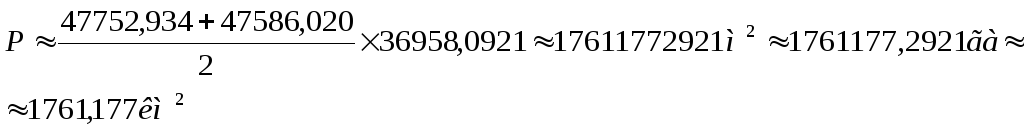
Вычисление диагонали съемочной трапеции.

Д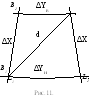иагональ съемочной трапециивычисляют по формуле:

(5.6)

где:

d – длина диагонали трапеции,

ΔY_Н – длина дуги параллели нижней рамки, ΔY_В– длина дуги параллели верхней рамки трапеции,

ΔХ – длина дуги меридиана левой (правой) рамки.

Задание 5.4 Вычислить диагональ съёмочной трапеции ограниченной параллелями с широтами B₁=31°00' и B₂=31°20' и меридианами с долготами L₁=66°00' и L₂=66°30'.

Решение