
- •Ministry of education and science of ukraine
- •Module structure Module № 1. „ Electrical current and magnetic field of a current” – 72 hours total
- •List of laboratory works
- •Introduction
- •Далее Лаб 2.1 и 3.4
- •3.2. Work of electrostatic field forces
- •3.3. Field potential. Difference of potentials.
- •3.4. Graphical representation of electric field. Field lines and equipotential serfaces
- •3.5. Relation between intensity and potential
- •3.6. Vector of electric displacement
- •5. Data processing
- •6. Work execution order and experimental data analysis
- •7. Test questions
- •8. Content of the report
- •Laboratory work № 2-2
- •3.3. Kirchhoff’s rules
- •4.1. Condition of balance of bridge according to Ohm’s law
- •4.2. Condition of balance of bridge according to Kirchhoff rules
- •5. Data processing
- •6. Work execution order and experimental data analysis
- •7. Test questions
- •8. Content of the report
- •5) Equations for calculation:
- •7) Quantities calculation: …
- •3.1. Ohm’s law for various circuit units
- •4. Description of laboratory research facility and methodology of measurements
- •4.1. Measurement of emf of a source with the compensation method
- •4.2. Measurement of emf of a source by direct method
- •5. Data processing
- •6. Work execution order and experimental data analysis
- •5.1. Compensation method
- •5.2. Direct method
- •7. Test questions
- •8. Content of the report
- •7) Calculation of quantities:
- •7.1) Compensation method:
- •7.2) Direct measurement method:
- •Laboratory work № 2-4
- •3.2. Dependence of total power, useful power and efficiency of a source from the external load resistance. Maximal power theorem
- •3.3. Dependence of total power, useful power and efficiency of the source from a current
- •4. Description of laboratory research facility and methodology of measurements
- •5. Data processing
- •6. Work execution order and experimental data analysis
- •7. Test questions
- •8. Content of the report
- •7) Calculation of quantities:
- •Here, l – is the length of midline of a torus.
- •3.2. Earth’s magnetic field
- •4. Description of laboratory research facility and methodology of measurements
- •5. Data processing
- •6. Work execution order and experimental data analysis
- •7. Test questions
- •8. Content of the report
- •3.2. Magnetic Properties of different materials
- •Magnetic Properties of different materials
- •Diamagnetism
- •Paramagnetism
- •Ferromagnetism
- •Hysteresis
- •Hysteresis loop
- •4 Description of laboratory research facility and methodology of measurements
- •6) Table of measurements
- •7) Calculation of quantities and their errors
- •9) Final results :
- •10) Conclusions:
- •Bibliography
- •Physics
7) Calculation of quantities:
|
8) Final results:
Plots of dependences of:
- total power PT , - useful power PU and - efficiency η
versus load resistance R: |
|
9) Conclusions:
9a) With increasing of load resistance the total power …
9b) With increasing of load resistance the efficiency …
9c) Useful power has a … , when … , therefore optimal mode with greatest delivery to external resistance corresponds to load matching condition … .
10) Data: “___” _____20___. Work done by: ______ Work checked by:
(Surname, readable)
LABORATORY WORK № 3-1
1. Topic: STIDYING MAGNETIC FIELD VIA TANGENT-COMPASS
2. Goal of the work:
2.1. Study of method of a vector diagrams for representation of magnetic field.
2.2. Finding the horizontal component of a magnetic intensity vector in the laboratory via tangent-compass.
3. Main concepts
3.1. Magnetic field of currents. Intensity and induction of magnetic field
Any moving electric charge creates a magnetic field. Electric current (as an ordered motion of charges) creates a magnetic field too. Magnetic field around a permanent magnet is being created by orientation in one direction of atomic micro-currents of material of magnet.
In the magnetic field other moving charge (or current) experiences a force. Thus wires with parallel currents are being attracted and with anti-parallel are being repulsed, because the magnetic field of moving charges of first wire acts on moving charges of the second wire.
As the objects of interaction in magnetism usually consider or moving electric charges or elements of current.
Element of the current Idl – is a product of a current I and infinitesimal segment of wire dl. Element of current is a vector, whose direction coincides with direction of the current. Element of current in Magnetism is similar to test charge in Electrostatics – it is a probe with the help of which we can explore magnetic field. As it has been established by Ampere, any element of the current, placed in a magnetic field B, will experience a force:
![]() ,
or, in scalars ,
,
or, in scalars ,
![]() .
(84)
.
(84)
Fig.
23
– Left
hand rule
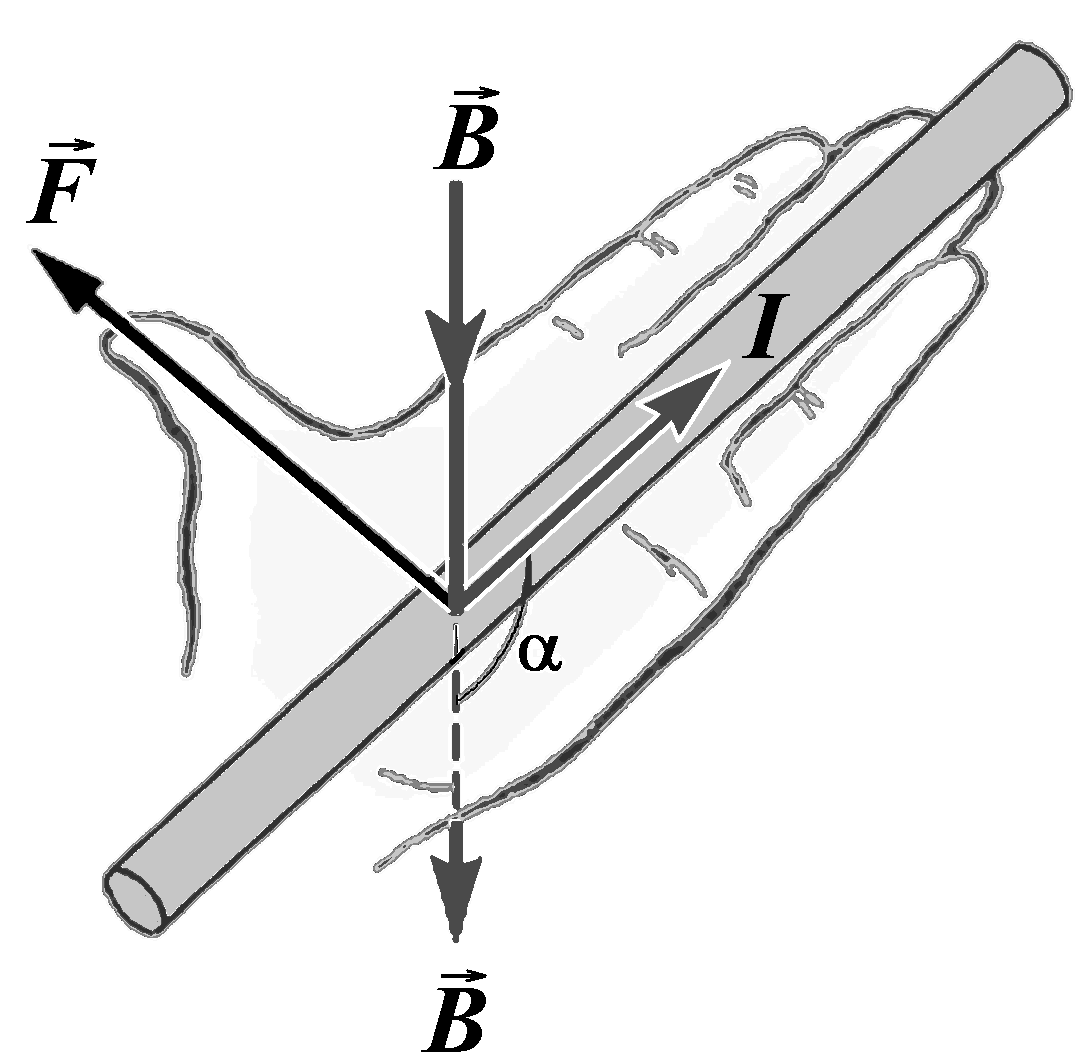
![]() .
Its direction defines by a “left
hand rule”: if
you place left hand so that four fingers point the direction of
current (see Fig.
23), and
vector of magnetic induction
.
Its direction defines by a “left
hand rule”: if
you place left hand so that four fingers point the direction of
current (see Fig.
23), and
vector of magnetic induction
![]() falls into open palm, then extended thumb points in the direction of
Ampere’s force.
falls into open palm, then extended thumb points in the direction of
Ampere’s force.
Quantity
![]() is a vector of magnetic induction. It has same direction as a force,
with which magnetic field acts on a north pole of magnetic arrow.
is a vector of magnetic induction. It has same direction as a force,
with which magnetic field acts on a north pole of magnetic arrow.
Equation (84) gives us a definition of magnetic induction:
![]() =>
=>
![]() ;
[B]=T.
(85)
;
[B]=T.
(85)
Vector of magnetic induction
numerically equals to force, with which
magnetic field acts on a unit element of current
(Idl=1Am),
placed perpendicularly to vector of
magnetic induction (when
![]() ).
).
Fig.
24
– Corkscrew
(right-hand
screw)
rule

![]() is Tesla. Tesla is the induction of
such magnetic field which exerts a force of 1N
on element of a current of 1 Am,
placed perpendicularly to vector
is Tesla. Tesla is the induction of
such magnetic field which exerts a force of 1N
on element of a current of 1 Am,
placed perpendicularly to vector
![]()
1T = 1N / 1Am.
Graphically
magnetic field can be depicted with the help of magnetic field lines
(lines of magnetic force). Magnetic
field line is
a type of line for which the tangent line to the path at each point
is parallel to the vector
![]() at
that point.
at
that point.
In order to determine direction of vector B the corkscrew rule (Fig. 24) is used: if translational motion of screw coincides with current I, then rotational motion point out a direction of magnetic field lines B.
Each element of a current generates a magnetic field around it. Induction of that field defines by Biot-Savart-Laplace law:
![]() ,
or, in scalars,
,
or, in scalars,
![]() ,
(86)
,
(86)
Fig.
25 –
Illustration
to the Biot-Savart-Laplace
law

![]() is being computed (Fig. 25);0=4
∙10–7H/m
– magnetic constant (permeability of vacuum);
– relative permeability of medium, it shows in what many times
induction in a given medium is different from that of vacuum.
is being computed (Fig. 25);0=4
∙10–7H/m
– magnetic constant (permeability of vacuum);
– relative permeability of medium, it shows in what many times
induction in a given medium is different from that of vacuum.
Quantity
![]() depends on medium, because certain substance magnetizes in external
magnetic field and generates certain own magnetic field.
depends on medium, because certain substance magnetizes in external
magnetic field and generates certain own magnetic field.
If we divide equation (86) on 0 we’ll obtain quantity, which is independent from properties of medium – magnetic intensity:
![]() .
(87)
.
(87)
Equation (87) is a Biot-Savart-Laplace law for magnetic intensity. It defines the value of magnetic field intensity dH for the field, generated by element of the current Idl. Therefore a definition of magnetic intensity:
![]() .
[H]=
.
[H]=![]() .
(88)
.
(88)
The SI unit for magnetic intensity is ampere per meter.
Directions
of
![]() and
and![]() coincide only in isotropic homogeneous medium or in nonmagnetic
material.
coincide only in isotropic homogeneous medium or in nonmagnetic
material.
If
wire has a complex shape (see fig. 25) it can be represented as a
huge number of elements of current Idl.
Resultant magnetic intensity (or induction) at any point is a vector
sum of elementary intensities
![]() (or
inductions
(or
inductions![]() )
of fields created by each element of currentIdl
individually:
)
of fields created by each element of currentIdl
individually:
![]() ;
;
![]() .
.
This superposition principle allows determine intensity (or induction) of field, created by wires with different form.
Magnetic intensity characterizes only magnetic field of macroscopic currents, because it don’t depend on magnetic properties of medium. Now, let’s consider some special cases.
3.1.1. Finite segment of current create a circular magnetic field (Fig.26). Magnetic intensity at a distance of r from axis of a current defined with the formula:
![]() ,
(89)
,
(89)
Fig.
26 – Field lines of segment of a current and corkscrew
rule


Vectors
of magnetic intensity
![]() and induction
and induction![]() are perpendicular to a plane passing through a segmentBC
and point A.
are perpendicular to a plane passing through a segmentBC
and point A.
Magnetic field lines are concentric circles around a straight current which are lying in perpendicular plane to a current. Direction of field lines can be determined by the corkscrew rule (Fig. 26): if translational motion of screw coincides with current I, then rotational motion point out a direction of magnetic field lines H.
3.1.2. Infinite straight current create a magnetic field same as a segment (Fig. 27).
If length of a segment (Fig.26) increases then angles α1 and α2 will decrease until they become zero as in the case of infinite wire. As cos 0° = 1, then
НA = I / 2r. (90)
Fig.
27 – Field lines of an infinite current

![]() and
field lines are the same as for finite segment (Fig.27).
and
field lines are the same as for finite segment (Fig.27).
3.1.3. Circular current (single coil) (Fig.28). Magnetic intensity at the center of a circular current can be defined with the formula
НC = I / 2R, (91)
Fig.
28 – Field lines of a circular current
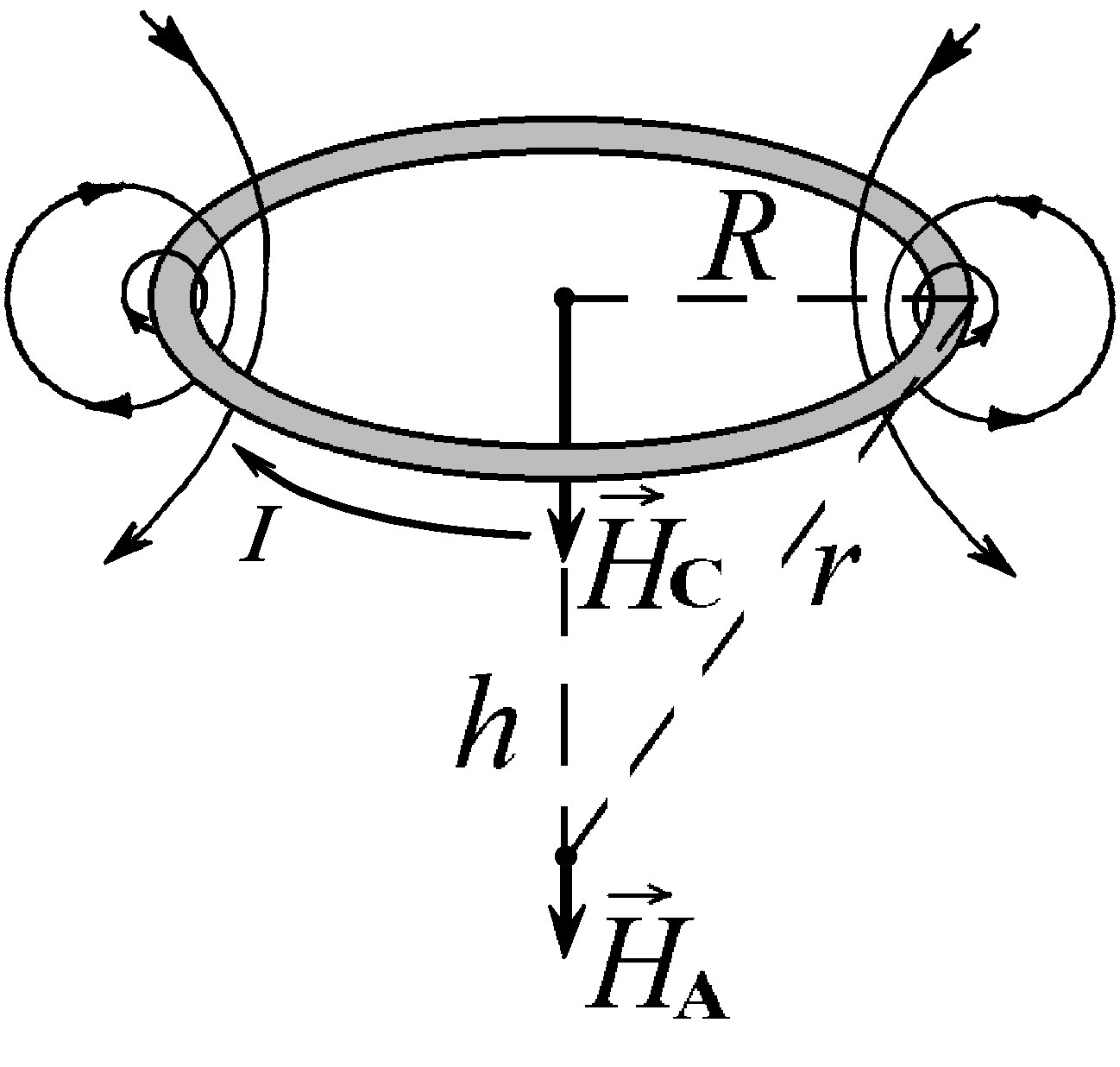
![]() is perpendicular to the plane of a coil in each point underlying in a
plane of that coil. It can be derived from superposition principle
applied to set of magnetic fields produced by each segment of wiredl
separately.
is perpendicular to the plane of a coil in each point underlying in a
plane of that coil. It can be derived from superposition principle
applied to set of magnetic fields produced by each segment of wiredl
separately.
Intensity magnitude on the axis of the circle can be defined with the formula
HA = IR2 / 2(R+h) 3 / 2, (92)
where h – distance from the point in which the field is being calculated to the center of coil.
3.1.4. Solenoid. (Fig.29) is a wire, wound around a cylindrical core. Length of a solenoid is in many times greater than its diameter. Inside the solenoid magnetic field there is uniform with intensity
H = IN / l = In, (93)
Fig.
29 – Field lines of solenoid

![]() field lines can be defined in the same way as in the case of single
coil.
field lines can be defined in the same way as in the case of single
coil.
Fig.
30 – Torus

![]() field lines are concentric circles. If the diameter of loopsD
is in many times smaller than the length of torus circle, the
intensity can be defined with the formula (50):
field lines are concentric circles. If the diameter of loopsD
is in many times smaller than the length of torus circle, the
intensity can be defined with the formula (50):
Н = IN / l = Iп, (93)

